Урок "Тотожні перетворення виразів, що містять квадратний корінь"
Тема. Тотожні перетворення виразів, що містять квадратний корінь
Мета: домогтися засвоєння учнями схем виконання дій під час перетворення цілих виразів, що містять квадратний корінь; сформувати вміння застосовувати вивчені схеми для розв'язування завдань на перетворення виразів, що містять квадратний корінь, які відповідають вимогам чинної програми з математики; виховувати бажання досягати успішного результату під час виконання поставлених завдань.
Тип уроку: застосування знань, умінь та навичок.
Наочність та обладнання: опорний конспект «Перетворення ірраціональних виразів».
Хід уроку
I. Організаційний етап
II. Перевірка домашнього завдання
Перевірка домашнього завдання у формі «Знайди помилку». На дошці записані чотири завдання з «допущеними помилками». Учні відшуковують помилку і коментують її. У разі необхідності складні та спірні моменти обговорюються.
|
Не правильний запис |
Правильний запис |
|
|
|
|
-0,3
-0,3*20 |
-0,3 -0,3*12*10=-36 |
|
3 |
3 |
|
-10 |
-10 |
III. Формулювання мети і завдань уроку
Учні самі дійдуть до розуміння проблеми, яку необхідно розв'язати на уроці, якщо поставити перед ними дані завдання.
Завдання 1
Виконайте дії: 12а + 4а; (a – 1)(a + 1); (1 + 2а)(2 – а) + 3а.
Завдання 2
Виконайте дії: ![]() ;
; ![]() ;
; ![]() .
.
Якщо з розв'язанням першого завдання в учнів проблем не виникає, то з другим завданням швидше за все учні не впораються (слід нагадати учням, що, виконуючи дії з коренями, слід спиратись тільки на вивчені властивості та схеми дій). Тому, порівнявши обидва завдання, учні доходять висновку про недостатність знань щодо означення та властивостей арифметичного квадратного кореня, вивчених на попередніх уроках; учні мають усвідомити необхідність оволодіння такими способами дій, що дозволять, використовуючи вивчені властивості квадратного кореня та вміння перетворювати раціональні вирази, виконувати перетворення виразів, що містять корені.
Таким чином формулюється основна дидактична мета уроку.
IV. Актуалізація опорних знань та вмінь
Необхідно активізувати такі знання і вміння учнів: первинні вміння виносити
множник з-під знака кореня та вносити множник під знак кореня; виконання
тотожних перетворень цілих раціональних виразів; застосування основної
тотожності для квадратного кореня.
Виконання усних вправ
-
Знайдіть значення виразу:
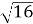 *
*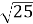 ;
; 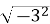 ;
; 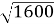 .
.
-
Подайте у вигляді
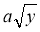 вираз:
вираз: 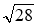 ;
; 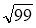 ;
; 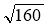 .
.
V. Застосування знань
Увесь зміст нового матеріалу представлений опорними прикладами
розв'язування завдань на перетворення цілих виразів, що містять арифметичний
квадратний корінь.
Для кращого розуміння учнями змісту перетворень запропонувати виконати записи у вигляді порівняльної таблиці, в якій розглянути спочатку приклад на перетворення цілого раціонального виразу, а потім приклад на відповідне перетворення цілого ірраціонального виразу (виразу, що містить квадратний корінь). Ця таблиця може мати такий вигляд:
|
Вид
Перетворення |
Цілий раціональний вираз |
Цілий ірраціональний вираз |
|
Зведення подібних доданків |
12а + 4а = (12 + 4)а = 16а |
12
= 16 |
І так далі...
VI. Формування вмінь
Виконання усних вправ
- Спростіть вираз:
а) ![]() ; б)
; б)![]() ; в)
; в) ![]() ;
;
г) ![]() .
.
- Розкладіть на множники:
а) ![]() ; б)
; б)![]() ; в) с2 – 2; г)
; в) с2 – 2; г)![]() ; д)
; д)![]() ; є)
; є) ![]() .
.
Виконання письмових вправ
На боковій дошці табличка
|
3 |
27 |
6 |
Х |
|
-26 |
0 |
4 |
-2 |
|
7 |
6 |
1 |
4 |
За виразом з кожної комірки заховане слово. Виконавши завдання, учень замінює комірку з виразом на комірку зі словом. Таким чином, отримується розшифрований вислів Норберта Вінера: «Найвище призначення математики полягає в тому, щоб знаходити прихований порядок в хаосі, що нас оточує».
Завдання (знайти значення виразу):
-
 2)
2)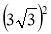
3) ![]() 4)
4) ![]()
5) ![]() 6)
6) ![]()
7) ![]() 8)
8) ![]()
9) ![]() 10)
10) ![]()
11) ![]() 12)
12) ![]()
Відповідність між виразом і зашифрованим словом:
3![]() – найвище, -26 – в тому, щоб; 7 – прихований, 27 – призначення,
– найвище, -26 – в тому, щоб; 7 – прихований, 27 – призначення,
0 – знаходити, 6 – що нас, 6![]() – математики, 4 – прихований,
– математики, 4 – прихований,
1 – оточує. , х – полягає, -2 – порядок, 4![]() +8 – Н. Вінер.
+8 – Н. Вінер.
Додаткове завдання:
В якому з випадків правильно виконано дію?
а) ![]() ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) ![]() .
.
VII. Підсумки уроку. Оцінювання учнів
Сьогодні на уроці, я дізнався…
VIII. Домашнє завдання
- Прочитати теоретичний матеріал підручника § 18.
- Розв'язати вправи на закріплення умінь, сформованих на уроці
368, 370.
1


про публікацію авторської розробки
Додати розробку
