Урок у 5 класі на тему: "Кут. Позначення кутів"

Тема. Кут. Позначення кутів

Мета. Формувати поняття: «кут», «вершина кута», «сторони кута», «бісектриса кута»; ознайомити з позначенням кутів; формувати вміння будувати кут і позначати його різними способами.

Тип уроку. Урок засвоєння нових знань.

Обладнання. Лінійка, паперові моделі кутів (12 штук).

Література:

• Для вчителя:

Істер О.С. Математика:підруч. для 5-го кл. загальноосвіт. навч. закл. / О.С. Істер. – К.: Генеза, 2013. – 368 с.: іл..

Слєпкань З.І. Методика навчання математики: Підручник. – 2-е вид., допов. і переробл. / З.І. Слєпкань. – К.: Вища шк., 2006. – 582 с.

• Для учнів:

Істер О.С. Математика:підруч. для 5-го кл. загальноосвіт. навч. закл. / О.С. Істер. – К.: Генеза, 2013. – 368 с.: іл..

Хід уроку

1. Організаційний етап.

Проконтролювати, щоб учні підготували класну дошку. Перевірка готовності учнів до уроку.

Сіли, діти, всі рівненько,

Посміхніться всі дружненько.

Урок математики ми починаємо,

І в Країну Знань вирушаємо!

2. Перевірка домашнього завдання.

Домашню роботу перевіряю за готовими відповідями, оцінюю.

3. Формулювання мети і завдань уроку.

Тема нашого уроку це «Кут. Позначення кутів». Дана тема для нас є новою, хоча деякі знання у вас повинні бути із початкової школи. Сьогодні ми їх пригадаємо та поглибимо. Тож відповідно до нашої теми метою уроку є:

1. Вивчити означення кута;
2. Навчитися будувати та позначати кути;
3. Вивчити означення бісектриси кута.
4. Навчитися будувати бісектрису кута.

(Девіз уроку роздрукований висить на класній дошці). Девіз нашого уроку: «Не кажи «не вмію», а кажи «навчусь».

4. Актуалізація опорних знань.

(Завчасно на зворотній частині дошки підготував рисунки).

Розгортаю зворотну частину дошки та задаю запитання:

1. Назвіть пари променів, які мають спільний початок:

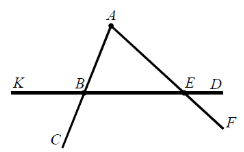
2. Які з променів перетинають промені AB і AD?

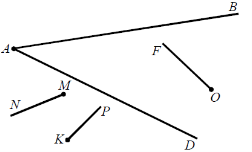
5. Вивчення нового матеріалу.

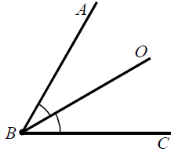
Задиктовую учням означення кута та одночасно рисую кут на дошці: кут – це геометрична фігура, утворена двома променями, які виходять з однієї точки.

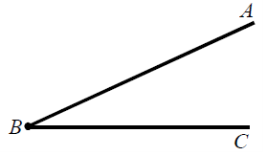
Точка В називається вершиною кута, а промені ВА і ВС – сторонами кута. Кут позначають:

а) однією буквою, якою позначена вершина кута, наприклад «кут В».

б) трьома буквами, якщо на променях позначені точки (буква, що позначає вершину, має бути посередині), наприклад, «кут АВС».

У запису замість слова «кут» використовують знак «».

Поняття променя, що проходить між сторонами кута.

Повинно виконуватися 2 умови:

1. промінь виходить з вершини кута;
2. він проходить між сторонами кута, тобто будь-який відрізок з кінцями на сторонах кута буде перетнутий цим променем.

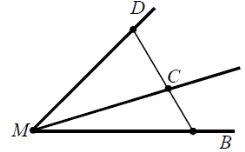
Якщо всередині кута DМВ взяти точку С і з вершини М провести через неї промінь, то він розіб’є кут DМВ на два кути — DМС і СМВ. Кут DМС менший від кута DМВ і кут СМВ менший від кута DМВ. У сумі кути DМС і СМВ становлять кут DМВ.

Два кути називають рівними, якщо вони суміщаються при накладанні.

Поняття бісектриси кута.

Бісектриса кута – це промінь, який виходить з вершини кута і ділить кут на дві частини рівних між собою.

Наприклад, — бісектриса, . У даному випадку позначати кути однією буквою не можна, бо при одній вершині є три кути.

6. Закріплення знань. Формування вмінь.

Усні вправи:

1. Назвіть вершину кута: , , , , .
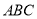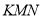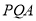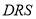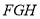2. Назвіть сторони кута: , , , , .

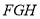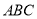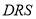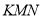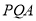Задачі № 640, 641 (за підручником О.С. Істер).

Практичне завдання

(Заздалегідь підготував паперові моделі кутів).

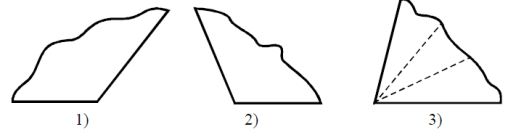
Завдання 1.

Як на моделі кута 1) можна побудувати бісектрису кута?

Перегнути так, щоб утворились два кути, які суміщаються. Лінія перегину — бісектриса.

Завдання 2.

Як розділити кут 2) на 4 рівних частини. Перегнути так, як у завданні 1, а потім утворений кут перегнути ще раз так само.

Завдання 3.

На моделі 3) проведено два промені так, що, перегнувши кути по цих променях, отримаємо 3 кути, які збігаються при накладанні. Чи можна промені, позначені на моделі, назвати бісектрисами даного кута? Чому? Чи є вони бісектрисами якихось інших кутів?

7. Підсумок уроку.

Запитання до класу:

1. Дайте визначення кута.
2. Як позначають кут?
3. Що таке бісектриса?
4. Яким чином можна побудувати бісектрису?

8. Домашнє завдання

§ 19 стор. 140, № 648, 656