"Збірник завдань на відповідність"
1
Часовоярська загальноосвітня школа І – ІІІ ступенів № 17
Бахмутської районної ради
Донецької області
Збірник завдань
на відповідність.
Учитель Любоженко Алла Георгіївна
Математика, 5 клас.
2019 – 2020 навчальний рік.
Вступ
Збірник завдань на відповідність складено як посібник для вчителів, що працюють у 5 класі за навчальною програмою для учнів 5 – 9 класів загальноосвітніх закладів. 2019 – 2020 навчальний рік.
Завдання підібрано та складено з десяти тем, що вивчаються у 5 класі за новим державним стандартом.
Вони можуть використовуватись для індивідуальної роботи з окремими учнями, для роботи в групах, як додатковий дидактичний матеріал при вивченні чи закріпленні відповідної теми, при написанні самостійних робіт.
До збірника ввійшли завдання різних рівнів. «![]() » позначені завдання початкового та середнього рівнів, «
» позначені завдання початкового та середнього рівнів, «![]() » - завдання достатнього рівня, «
» - завдання достатнього рівня, «![]() » - завдання високого рівня навчальних досягнень.
» - завдання високого рівня навчальних досягнень.
Окрім власних завдань, укладач використовував завдання з підручників, збірників та посібників для вчителів авторів О. С. Істер, Н. А. Тарасенкової, А. Г. Мерзляка, Г. П. Бевза та інших.
Тема 1. Натуральні числа.
![]() Установити відповідність між числами та їх назвами:
Установити відповідність між числами та їх назвами:
- 908 200; А. дев’ять мільйонів вісімсот двадцять;
- 9 000 820; Б. дев’ятсот вісім тисяч двісті;
- 9 000 082; В. дев’ятсот мільярдів вісімдесят два;
- 900 800 002; Г. дев’ять мільйонів вісімдесят два;
Д. дев’ятсот мільйонів вісімсот тисяч два.
2. ![]() Установити відповідність між числами та їх назвами:
Установити відповідність між числами та їх назвами:
1. 307 100; А. три мільйони сімсот десять;
2. 3 000 710; Б. триста сім тисяч сто;
3. 3 000 071; В. триста мільярдів сімдесят один;
4. 300 700 001; Г. три мільйони сімдесят один;
Д. триста мільйонів сімсот тисяч один.
3.![]() Установити відповідність між іменованими числами, що виражені різними одиницями виміру, так, щоб вони були рівними:
Установити відповідність між іменованими числами, що виражені різними одиницями виміру, так, щоб вони були рівними:
- 13 кг 5 г; А. 1035 кг;
- 130 кг 50 г; Б. 13005 г;
- 135 ц; В. 13 т 50 г;
- 10ц 35 кг; Г. 1 т 3 кг 5 г; Д. 13 т 500 кг.
4.![]() Установити відповідність між іменованими числами, що виражені різними одиницями виміру, так, щоб вони були рівними:
Установити відповідність між іменованими числами, що виражені різними одиницями виміру, так, щоб вони були рівними:
- 27 кг 9 г; А. 2079 кг;
- 270 кг 90 г; Б. 27009 г;
- 279 ц ; В. 27 т 90 г;
- 20 ц 79 кг; Г. 2 т 7 кг 9 г; Д. 27 т 900 кг.
5.![]() Установити відповідність між нерівностями та цифрами, які можна в них поставити замість «*», щоб нерівності були вірними:
Установити відповідність між нерівностями та цифрами, які можна в них поставити замість «*», щоб нерівності були вірними:
-
50 6*5
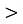 50 685; А. 0;
50 685; А. 0;
-
30 99* 999
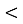 30 992 000; Б. 9;
30 992 000; Б. 9;
-
6 001
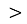 600* ; В. не можна вставити жодну цифру;
600* ; В. не можна вставити жодну цифру;
-
485 *10
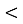 485 410; Г. 0; 1; Д. 0; 1; 2; 3.
485 410; Г. 0; 1; Д. 0; 1; 2; 3.
6.![]() Установити відповідність між нерівностями та цифрами, які можна в них поставити замість «*», щоб нерівності були вірними:
Установити відповідність між нерівностями та цифрами, які можна в них поставити замість «*», щоб нерівності були вірними:
-
20 7*9
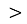 20 799; А. 1;
20 799; А. 1;
-
43 88* 888
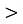 43 888 900; Б. не можна вставити жодну цифру;
43 888 900; Б. не можна вставити жодну цифру;
-
5 02 0
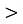 5 0*9; В. 0; 1;
5 0*9; В. 0; 1;
-
946 *10
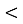 9 46 200; Г. 9;
9 46 200; Г. 9;
Д. можна вставити будь-яку цифру.
7.![]() На відрізку АВ вибрали точку С. Установити відповідність між відрізками АС і ВС та довжиною відрізка АВ:
На відрізку АВ вибрали точку С. Установити відповідність між відрізками АС і ВС та довжиною відрізка АВ:
- АС=12 см, ВС=7 см; А. АВ=16 см;
- АС=9 см, ВС=8 см; Б. АВ=19 см;
- АС=13 см, ВС=25 см; В. АВ=17 см;
- АС=39 см, ВС=16 см; Г. АВ=38 см; Д. АВ=55 см.
8.![]() На відрізку АВ вибрали точку С. Установити відповідність між відрізками АС і ВС та довжиною відрізка АВ:
На відрізку АВ вибрали точку С. Установити відповідність між відрізками АС і ВС та довжиною відрізка АВ:
- АС=32 см, ВС= 46 см; А. АВ= 42 см;
- АС=19 см, ВС=23 см; Б. АВ= 90 см;
- АС=56 см, ВС=34 см; В. АВ=78 см;
- АС=68 см, ВС= 17 см; Г. АВ= 57 см; Д. АВ=85 см.
Тема 2. Додавання та віднімання натуральних чисел. Числові і буквені вирази.
1. ![]() Установити відповідність між числовими виразами та їх значеннями:
Установити відповідність між числовими виразами та їх значеннями:
- 29 +11; А. 298;
- 321- 48; Б. 40;
- 1000 – 702; В. 901;
- 805 + 96; Г. 350; Д. 273.
2. ![]() Установити відповідність між числовими виразами та їх значеннями:
Установити відповідність між числовими виразами та їх значеннями:
1. 100 – 56; А. 71;
2. 359+ 45; Б. 44;
3. 2100 – 210; В. 404;
4. 712 + 88; Г. 1 890; Д. 800.
3. ![]() Установити відповідність між числами та їх характеристиками:
Установити відповідність між числами та їх характеристиками:
- 1; А. найменше чотирицифрове число;
- 99; Б. найменше натуральне число;
- 1 000; В. найбільше двоцифрове число;
- 555; Г. число, за яким іде 1 000 000;
Д. число, сума цифр якого дорівнює 15.
4. ![]() Установити відповідність між числами та їх характеристиками:
Установити відповідність між числами та їх характеристиками:
1. 2; А. Число, в якому 11 десятків.
2. 110; Б. Число, сума цифр якого дорівнює 15.
3. 999; В. Найменше парне натуральне число.
4. 438; Г. Найбільше трицифрове число.
Д. Число, що стоїть перед 2000.
5.![]() Установити відповідність між умовами задач та виразами, що складені до їх розв’язання:
Установити відповідність між умовами задач та виразами, що складені до їх розв’язання:
- Один художній альбом коштує 315 грн., а другий – на 47 грн. менше. Скільки коштують обидва альбоми разом?
- Сашко зібрав 26 грибів, Василько – на 15 грибів більше. Скільки грибів зібрали хлопці разом?
- Одна бригада відремонтувала за тиждень 43 км шляху, а друга – на 16 км менше. Скільки кілометрів відремонтували обидві бригади разом?
- У вагоні трамвая було54 пасажири. На зупинці вийшло 27 пасажирів, а ввійшло – 19. Скільки пасажирів стало у вагоні?
А. (43 - 16) + 43; Б. (54-27) + 19;
В. (315 - 47) + 314; Г. (26 + 15) + 26; Д. (43 + 16) – 43.
Вираз до якої задачі складено невірно?
6. ![]() Установити відповідність між задачами та виразами, що складені до їх розв’язання:
Установити відповідність між задачами та виразами, що складені до їх розв’язання:
- За перший тиждень Катруся прочитала 184 сторінки, а за другий – на 35 сторінок менше. Скільки сторінок прочитала Катруся за два тижні?
- На першій стоянці було 29 автомобілів, а на другій – на 14 більше. Скільки автомобілів було на обох стоянках разом?
- У першому кошику лежить 37 яблук, а в другому – на 19 яблук більше. Скільки яблук лежить в обох кошиках разом?
- У новому будинку 204 двокімнатних квартири, а трикімнатних на 36 менше. Скільки всього двокімнатних і трикімнатних квартир у новому будинку?
А. (204 – 36) + 204; Б. (37 + 19) + 37; В. (29 + 14) + 29; Г. (37 – 19) + 19; Д. (184 – 35) + 184.
Вираз до якої задачі складено невірно?
7.![]() Побудувати координатний промінь ОХ. Відкласти на ньому точки А, В і С за відомими координатами. Установити відповідність між даними точками та довжинами відповідних відрізків:
Побудувати координатний промінь ОХ. Відкласти на ньому точки А, В і С за відомими координатами. Установити відповідність між даними точками та довжинами відповідних відрізків:
- А(2), В(6), С(5); А. АВ+ВС =8;
- А(9), В(4), С(7); Б. АВ+ВС = 9;
- А(4), В(3), С(11); В. АВ – ВС =15;
- А(1), В(12), С(8); Г. АВ – ВС = 7; Д. АВ + ВС =5.
8.![]() Побудувати координатний промінь ОХ. Відкласти на ньому точки А, В і С за відомими координатами. Установити відповідність між даними точками та довжинами відрізків:
Побудувати координатний промінь ОХ. Відкласти на ньому точки А, В і С за відомими координатами. Установити відповідність між даними точками та довжинами відрізків:
- А(7), В(13), С(2); А. АВ + ВС = 7;
- А(6), В(9), С(13); Б. АВ – ВС = 4;
- А(8), В(16), С(9); В. АВ + ВС = 17;
- А(4), В(10), С(6); Г. АВ – ВС = 22. Д. АВ – ВС = 2
9.![]() Виконати дії зручним способом. Установити відповідність між виразами та їх значеннями:
Виконати дії зручним способом. Установити відповідність між виразами та їх значеннями:
- 36 + (14 +59); А. 143;
- (43 + 38) +62; Б. 25;
- 149 – (49 + 75); В. 239;
- 215 + (39 – 15); Г. 175; Д. 25.
10.![]() Виконати дії зручним способом. Установити відповідність між виразами та їх значеннями:
Виконати дії зручним способом. Установити відповідність між виразами та їх значеннями:
- 47 + (53 + 69); А. 175;
- (27 + 78) + 73; Б. 169;
- 259 – (59 + 25; В. 178;
- 138 + (96 – 38); Г. 225; Д. 196.
11. ![]() Установити відповідність між буквеними виразами та їх значеннями при заданих значеннях букв:
Установити відповідність між буквеними виразами та їх значеннями при заданих значеннях букв:
- 12х + 39, якщо х = 15; А. 2;
-
42
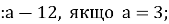 Б. 250;
Б. 250;
- 132 + 5х + 68, якщо х = 10; В. 260;
-
у
 (у +7), якщо у =13; Г. 2 050; Д. 219.
(у +7), якщо у =13; Г. 2 050; Д. 219.
12.![]() Установити відповідність між буквеними виразами та їх значеннями при заданих значеннях букв:
Установити відповідність між буквеними виразами та їх значеннями при заданих значеннях букв:
- 14х + 28, якщо х = 15; А. 5;
-
63
 а – 16 , якщо а = 3; Б. 290;
а – 16 , якщо а = 3; Б. 290;
- 146 + 9х + 54, якщо х = 10; В. 238;
-
в
 (в – 13), якщо в = 23; Г. 330; Д. 230.
(в – 13), якщо в = 23; Г. 330; Д. 230.
13. ![]() а м і в м – виміри (довжина та ширина) прямокутника, а S кв. м – його площа. Установити відповідність між вимірами та площею:
а м і в м – виміри (довжина та ширина) прямокутника, а S кв. м – його площа. Установити відповідність між вимірами та площею:
- а = 15 м, в = 14 м; А. 500 кв. м;
- а = 16 м, в = 25 м; Б. 210 кв. м;
- а = 35 м, в = 18 м; В. 400 кв. м;
- а = 49 м, в = 12 м; Г. 630 кв. м; Д. 588 кв. м;
14.![]() а м і в м – виміри (довжина і ширина) прямокутника, S кв. м – його площа. Установити відповідність між вимірами та площею:
а м і в м – виміри (довжина і ширина) прямокутника, S кв. м – його площа. Установити відповідність між вимірами та площею:
- а = 17 м, в = 15 м; А. 45 кв. м;
- а = 25 м, в = 18 м; Б. 255 кв. м;
- а = 38 м, в = 29 м; В. 450 кв. м;
- а = 54 м, в = 26 м; Г. 1102 кв. м; Д. 1404 кв. м.
15.![]() Установити відповідність між стороною а квадрата та його периметром Р:
Установити відповідність між стороною а квадрата та його периметром Р:
- а = 15 см; А. 84 см;
- а = 21 см; Б. 64 см;
- а = 16 см; В. 108 см;
- а = 27 см; Г. 225 см; Д. 60 см.
16.![]() Установити відповідність між стороною а квадрата та його периметром Р:
Установити відповідність між стороною а квадрата та його периметром Р:
- а =42 см; А. 140 см;
- а = 35 см; Б. 68 см;
- а = 17 см; В. 289 см;
- а = 26 см; Г. 168 см; Д. 104 см.
17.![]() Відомі шлях та час, за який його подолали. Знайти швидкість і встановити відповідність:
Відомі шлях та час, за який його подолали. Знайти швидкість і встановити відповідність:
- S = 156 км, t =3 год. А. v =45 км/год.
- S = 162 км, t = 9 год. Б. v = 128 км/ год.
- S = 180 км, t = 4 год. В. v = 52 км/год.
- S = 640 км, t =5 год. Г. v = 32 км/год. Д. v = 18 км/год.
18.![]() Відомі шлях та час, за який його подолали. Знайти швидкість і встановити відповідність:
Відомі шлях та час, за який його подолали. Знайти швидкість і встановити відповідність:
- S =256 км, t = 4 год. А. v = 64 км/год.
- S =365км, t = 5 год. Б. v = 70 км/год.
- S = 420 км, t = 6 год. В. v = 36 км/год.
- S = 497км, t = 7 год. Г. v = 73 км/год. Д. v = 71 км/год.
Тема 3. Множення та ділення натуральних чисел.
.![]() Установити відповідність між числовими виразами та їх значеннями:
Установити відповідність між числовими виразами та їх значеннями:
-
13
 25; А. 24 219;
25; А. 24 219;
-
408
 49; Б. 22 608;
49; Б. 22 608;
-
314
 72; В. 2 352;
72; В. 2 352;
-
299
 81; Г. 19 99; Д. 325.
81; Г. 19 99; Д. 325.
2.![]() Установити відповідність між числовими виразами та їх значеннями:
Установити відповідність між числовими виразами та їх значеннями:
-
24
 35; А. 2 223;
35; А. 2 223;
-
309
 57; Б. 24 118;
57; Б. 24 118;
-
225
 81;
81;  В. 840;
В. 840;
-
389
 62; Г. 18 225; Д. 17 613.
62; Г. 18 225; Д. 17 613.
3.![]() Установити відповідність між числовими виразами та їх значеннями:
Установити відповідність між числовими виразами та їх значеннями:
- 3 528 : 84; А. 406;
-
6 902
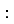 17; Б. 203;
17; Б. 203;
-
5 278
 26; В. 42;
26; В. 42;
-
18 564
 78; Г. 459; Д. 238.
78; Г. 459; Д. 238.
4.![]() Установити відповідність між числовими виразами та їх значеннями:
Установити відповідність між числовими виразами та їх значеннями:
-
2 888
 76; А. 503;
76; А. 503;
-
6 539
 13; Б. 38;
13; Б. 38;
-
5 712
 28; В. 308;
28; В. 308;
-
21 352
 68; Г. 204; Д. 314.
68; Г. 204; Д. 314.
5.![]() Обчислити зручним способом і установити відповідність між числовими виразами та їх значеннями:
Обчислити зручним способом і установити відповідність між числовими виразами та їх значеннями:
-
4
 13
13  25; А. 1 300;
25; А. 1 300;
-
125
 17
17  8; Б. 4 800;
8; Б. 4 800;
-
4
 24
24  50; В. 23 600;
50; В. 23 600;
-
5
 236
236  20; Г. 48 000; Д. 17 000.
20; Г. 48 000; Д. 17 000.
6.![]() Обчислити зручним способом і установити відповідність між числовими виразами та їх значеннями:
Обчислити зручним способом і установити відповідність між числовими виразами та їх значеннями:
-
5
 17
17  20; А. 457 000;
20; А. 457 000;
-
8
 37
37  125; Б. 2 700;
125; Б. 2 700;
-
50
 27
27  4; В. 45 700;
4; В. 45 700;
-
25
 457
457  40; Г. 37 000; Д. 1 700.
40; Г. 37 000; Д. 1 700.
7.![]() Обчислити зручним способом і установити відповідність між числовими виразами та їх значеннями:
Обчислити зручним способом і установити відповідність між числовими виразами та їх значеннями:
-
37
 218 + 63
218 + 63  218; А. 5 200;
218; А. 5 200;
-
568
 43 – 566
43 – 566  43; Б. 166 800;
43; Б. 166 800;
-
417
 187 + 417
187 + 417  213; В. 2;
213; В. 2;
-
52
 187 – 52
187 – 52 43 – 52
43 – 52 44; Г. 21 800; Д. 41 700.
44; Г. 21 800; Д. 41 700.
8.![]() Обчислити зручним способом і установити відповідність між числовими виразами та їх значеннями:
Обчислити зручним способом і установити відповідність між числовими виразами та їх значеннями:
-
405
 82 + 405
82 + 405  18; А. 100;
18; А. 100;
-
497
 38 – 496
38 – 496 38; Б. 40 500;
38; Б. 40 500;
-
344
 92 + 344
92 + 344  208; В. 1;
208; В. 1;
-
23
 48 – 35
48 – 35  23 + 87
23 + 87  23; Г. 103 200; Д. 2 300.
23; Г. 103 200; Д. 2 300.
9.![]() Розв’язати рівняння та встановити відповідність між цими рівняннями і їх коренями:
Розв’язати рівняння та встановити відповідність між цими рівняннями і їх коренями:
- х : 19 =26; А. 16;
- 238 : х = 14; Б. 234;
- х : 8 + 7 = 9; В. 17;
-
15
 (2х + 11) = 285; Г. 494; Д. 4.
(2х + 11) = 285; Г. 494; Д. 4.
10.![]() Розв’язати рівняння та встановити відповідність між цими рівняннями і їх коренями:
Розв’язати рівняння та встановити відповідність між цими рівняннями і їх коренями:
- х : 18 = 23; А. 318;
- 228 : х = 12; Б. 138;
- 360 : (х – 2) = 4; В. 19;
- х : 6 – 15 = 38; Г. 92; Д. 414.
11.![]() Скласти вирази до розв’язування задач і установити відповідність між задачами та виразами:
Скласти вирази до розв’язування задач і установити відповідність між задачами та виразами:
- З деякого міста в одному напрямі одночасно вирушили два автомобілі. Швидкість одного з них дорівнювала 48 км/год., а другого – 46 км/год. Якою буде відстань між ними через 6 годин після початку руху?
- З деякого міста в протилежних напрямках одночасно вирушили два автомобілі. Один з них рухався зі швидкістю 48 км/год., а другий – 64 км/год. Якою буде відстань між ними через 6 години після початку руху?
- З двох міст одночасно назустріч один одному вирушили два автомобілі зі швидкостями 48 км/год. і 46 км/год. Яка відстань між цими містами, якщо вони зустрілись через 6 годин після початку руху?
- З двох міст, відстань між якими 564 км, назустріч один одному вирушили два автомобілі і зустрілись через 6 годин. Швидкість одного з них дорівнює 48 км. Знайти швидкість другого автомобіля.
А. 564: 6 – 48; Б. (564 -48) : 6; В. (48 + 46)![]()
Г. (48 – 46) ![]() Д. (48 + 64)
Д. (48 + 64) ![]()
12.![]() Скласти вирази до розв’язування вправ і установити відповідність між вправами та цими виразами:
Скласти вирази до розв’язування вправ і установити відповідність між вправами та цими виразами:
- Суму чисел 28 та 49 збільшити у 7 разів.
- Різницю чисел 49 та 28 зменшити у 7 разів.
- Добуток чисел 49 та 28 збільшити у 7 разів.
- Добуток чисел 49 та 28 зменшити у 7 разів.
А. (49 – 28) : 7; Б. (49 ![]() ) : 7; В. ( 48 + 28)
) : 7; В. ( 48 + 28) ![]() 7;
7;
Г. (49 ![]() 27)
27) ![]() 7; Д. (49:28) : 7.
7; Д. (49:28) : 7.
13. ![]() Виконати ділення з остачею і установити відповідність між прикладами та остачею:
Виконати ділення з остачею і установити відповідність між прикладами та остачею:
- 36 : 7; А. 9;
- 490 : 15; Б. 19;
- 1309 : 20; В. 2;
- 258 : 16; Г. 10; Д. 1.
14.![]() Виконати ділення з остачею і установити відповідність між прикладами та остачею:
Виконати ділення з остачею і установити відповідність між прикладами та остачею:
- 43 : 7; А. 1;
- 553 : 18; Б. 16;
- 1406 : 30; В. 13;
- 295 : 17; Г. 26; Д. 6.
Тема 4. Рівняння. Розв’язування задач.
1.![]() Установити відповідність між рівняннями та їх коренями:
Установити відповідність між рівняннями та їх коренями:
- 48 + х = 123; А. 34;
- 247 – х = 89; Б. 75;
- Х – 63 = 128; В. 158;
-
17
 х = 578; Г. 336; Д. 191.
х = 578; Г. 336; Д. 191.
2.![]() Установити відповідність між рівняннями та їх коренями:
Установити відповідність між рівняннями та їх коренями:
- 39 + х = 156; А. 46;
- 318 – х = 97; Б. 281;
- х – 67 = 214; В. 415;
-
23
 х = 1058; Г. 221; Д. 116.
х = 1058; Г. 221; Д. 116.
3.![]() Розв’язати рівняння і установити відповідність між ними та їх коренями:
Розв’язати рівняння і установити відповідність між ними та їх коренями:
- 5х + 3х = 648; А. 93;
- 7х – 4х = 729; Б. 81;
- (у – 12) : 7 = 15; В. 243;
- 72 : (х + 9) = 3; Г. 117; Д. 15.
4.![]() Розв’язати рівняння і установити відповідність між ними та їх коренями:
Розв’язати рівняння і установити відповідність між ними та їх коренями:
- 7х + 8х = 225; А. 149;
- 14х – 5х = 999; Б. 15;
- (у – 35) : 8 = 23; В. 111;
- 63 : (х + 6) = 7; Г. 219; Д. 3.
5.![]() Скласти рівняння для розв’язку задач і встановити відповідність між задачами та рівняннями до них:
Скласти рівняння для розв’язку задач і встановити відповідність між задачами та рівняннями до них:
- За пальто та чоботи заплатили 2380 грн., причому пальто у 6 разів дорожче за чоботи. Скільки коштує пальто?
- За два вечірніх плаття заплатили 2380 грн., причому одне з них на 6 грн. дешевше від іншого. Скільки коштує дорожче вечірнє плаття?
- Меблі для вітальні на 2380 грн. дорожчі, ніж ліжко. Скільки коштують меблі для вітальні, якщо вони у 6 разів дорожчі за ліжко?
-
 За три дні продали 2380 кг картоплі, причому за перший день продали в 6 разів більше, ніж за другий, а за третій – на 6 кг менше, ніж за другий. Скільки кілограмів картоплі продали за другий день?
За три дні продали 2380 кг картоплі, причому за перший день продали в 6 разів більше, ніж за другий, а за третій – на 6 кг менше, ніж за другий. Скільки кілограмів картоплі продали за другий день?
А. 6х – х = 2 380;
Б. 6х + х + (х – 6) = 2 380;
В. х + (х – 6) = 2 380; Г. 6х + х – 6 = 2 380; Д. 6х + х = 2 380.
6.![]() Скласти рівняння за умовами задач і встановити відповідність між задачами та рівняннями до них:
Скласти рівняння за умовами задач і встановити відповідність між задачами та рівняннями до них:
- Тетяна задумала число. Якщо це число збільшити у 2 рази і отриманий результат зменшити на 35, то отримаємо 185. Яке число задумала Тетяна?
- Андрій до задуманого числа додав 35, потім результат зменшив у два рази і отримав 185. Яке число задумав Андрій?
-
 У дідуся запитали про його вік. Він відповів на запитання так: «Якщо до моїх років додати мої подвоєні роки та ще 35, то вийде 185». Скільки років дідусеві?
У дідуся запитали про його вік. Він відповів на запитання так: «Якщо до моїх років додати мої подвоєні роки та ще 35, то вийде 185». Скільки років дідусеві?
- Якщо задумане число збільшити на 2, а потім результат зменшити у 35 разів, то вийде 185. Знайти це число.
А. (х + 2) : 35 = 185;
Б. (х + 35) : 2 = 185;
В. 2х – 35 = 185; Г. х + 2х + 35 = 185; Д. 35х – 2 = 185.
7.![]() Розв’язати рівняння та порівняти їх корені. Установити відповідність:
Розв’язати рівняння та порівняти їх корені. Установити відповідність:
-
2х + 3х – 15 = 65 і х + 4х = 80; А. 22
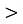 5;
5;
-
38 : (х – 6) =2 і (х – 5) : 8 = 2; Б. 6
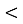 10;
10;
-
3х – (16 + х) = 28 і (9х + 14) – 12 = 47; В. 13
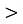 11;
11;
-
(4х – 8)
 3 = 48 і (25 – 2х)
3 = 48 і (25 – 2х)  7 = 35; Г. 25
7 = 35; Г. 25 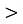 21;
21;
Д. корені рівні по 16.
8.![]() Розв’язати рівняння та порівняти їх корені. Установити відповідність:
Розв’язати рівняння та порівняти їх корені. Установити відповідність:
-
6х – х = 70 і 12х – х = 154; А. 9
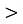 3;
3;
-
72: х + 5 = 13 і 54 : х – 7 = 11; Б. 6
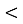 15;
15;
-
6х – (2х – 25) = 39 і (8х – 5х) + 42 = 99; В. 15
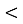 19;
19;
-
(5х – 9)
 3 = 63 і ( 57 – 3х)
3 = 63 і ( 57 – 3х)  9 = 108; Г. корені рівні по 14;
9 = 108; Г. корені рівні по 14;
Д. 4 ![]() 36.
36.
Тема 5. Степінь натурального числа з натуральним показником. Площі та об’єми фігур.
1.![]() Установити відповідність між виразом та його значенням:
Установити відповідність між виразом та його значенням:
-
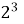 +
+ 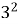 ; А. 37;
; А. 37;
-
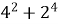 ; Б. 19;
; Б. 19;
-
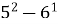 ; В. 4;
; В. 4;
-
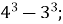 Г. 32; Д. 17.
Г. 32; Д. 17.
2.![]() Установити відповідність між виразом та його значенням:
Установити відповідність між виразом та його значенням:
-
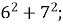 А. 181;
А. 181;
-
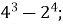 Б. 8;
Б. 8;
-
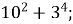 В. 4;
В. 4;
-
 ; Г. 48; Д. 85.
; Г. 48; Д. 85.
3.![]() Знайти значення виразів та установити відповідність між виразами та їх значеннями:
Знайти значення виразів та установити відповідність між виразами та їх значеннями:
-
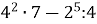 ; А. 5;
; А. 5;
-
3
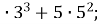 Б. 221;
Б. 221;
-
24:
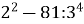 ; В. 68;
; В. 68;
-
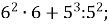 Г.104; Д. 206.
Г.104; Д. 206.
4.![]() Знайти значення виразів та установити відповідність між виразами та їх значеннями:
Знайти значення виразів та установити відповідність між виразами та їх значеннями:
-
9
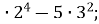 А. 216;
А. 216;
-
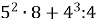 ; Б. 99;
; Б. 99;
-
(
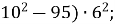 В. 65;
В. 65;
-
(
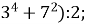 Г. 180; Д. 13.
Г. 180; Д. 13.
5.![]() Установити відповідність між довжинами у різних одиницях виміру:
Установити відповідність між довжинами у різних одиницях виміру:
- 26 дм; А. 260 дм;
- 26 м; Б. 260 см;
- 26 см; В. 26 000 м;
- 26 км; Г. 2 600 дм; Д. 260 мм.
6.![]() Установити відповідність між площами у різних одиницях виміру:
Установити відповідність між площами у різних одиницях виміру:
-
4
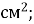 А. 400
А. 400 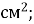
-
4
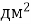 ; Б. 40 000
; Б. 40 000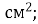
-
4
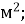 В. 400
В. 400 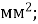
-
4
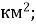 Г. 4 000 000
Г. 4 000 000 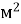 ; Д. 4 000
; Д. 4 000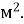
7.![]() Установити відповідність між об’ємами у різних одиницях виміру:
Установити відповідність між об’ємами у різних одиницях виміру:
-
5
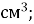 А. 50 000
А. 50 000 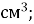
-
500
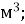 Б. 500
Б. 500 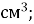
-
50
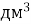 ; В. 5 000
; В. 5 000 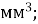
-
50 000
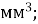 Г. 500
Г. 500 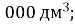 Д. 5 000
Д. 5 000 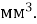
8.![]() Обчислити площу прямокутника і встановити відповідність між довжиною, шириною та площею прямокутника:
Обчислити площу прямокутника і встановити відповідність між довжиною, шириною та площею прямокутника:
-
а = 7 см, в = 12 см; А. 120
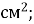
-
а = 9 см, в = 11 см; Б. 84
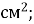
-
а =15 см, в = 8 см; В. 99
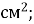
-
а = 18 см, в = 5 см; Г. 40
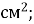 Д. 90
Д. 90 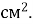
9.![]() За даними площею та довжиною прямокутника знайти його ширину. Установити відповідність:
За даними площею та довжиною прямокутника знайти його ширину. Установити відповідність:
-
а = 14 см, S = 56
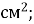 А. в = 11 см;
А. в = 11 см;
-
а = 9 см, S = 72
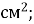 Б. в = 4 см;
Б. в = 4 см;
-
а = 13 см, S = 910
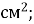 В. в = 7 см;
В. в = 7 см;
-
а = 12 см, S = 132
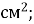 Г. в = 8 см; Д. в =70 см.
Г. в = 8 см; Д. в =70 см.
10.![]() Розв’язати задачу і встановити відповідність між умовою та відповіддю:
Розв’язати задачу і встановити відповідність між умовою та відповіддю:
-
Знайдіть периметр квадрата, площа якого дорівнює 49
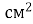 .
.
- Знайдіть площу квадрата, периметр якого дорівнює 36 см.
- Довжина прямокутника 24 см, що в 3 рази більше за ширину. Знайдіть площу прямокутника.
-
Знайдіть довжину прямокутника, якщо вона у два рази більша за ширину, а площа дорівнює 96
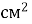 .
.
А. 64 см; Б. 81 ![]() ; В. 28 см; Г. 192
; В. 28 см; Г. 192 ![]() Д. 48 см.
Д. 48 см.
11.![]() Дано виміри прямокутного паралелепіпеда. Установіть відповідність між вимірами та об’ємом:
Дано виміри прямокутного паралелепіпеда. Установіть відповідність між вимірами та об’ємом:
-
4 см; 6 см; 12 см; А. 280
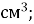
-
5 см; 7 см; 8 см; Б. 2 500
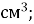
-
3 см; 9 см; 10 см; В. 288
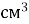 ;
;
-
11 см; 15 см; 20 см; Г. 3 300
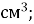 Д. 270
Д. 270 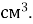
12.![]() Знайдіть об’єм куба за відомою площею його грані. Установіть відповідність між площею грані куба та його об’ємом:
Знайдіть об’єм куба за відомою площею його грані. Установіть відповідність між площею грані куба та його об’ємом:
-
36
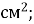 А. 343
А. 343 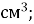
-
81
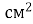 ; Б. 1 000
; Б. 1 000 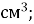
-
100
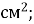 В. 216
В. 216 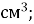
-
49
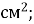 Г. 400
Г. 400 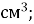 Д. 729
Д. 729 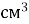 .
.
13. ![]() Установіть відповідність між ребром куба а та площею його поверхні S:
Установіть відповідність між ребром куба а та площею його поверхні S:
-
а = 3 м; А. S = 600
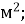
-
а = 5 м; Б. S = 1 000
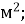
-
а = 7 м; В. S = 54
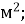
-
а = 10 м; Г. S = 294
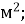 Д. S = 150
Д. S = 150 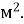
Тема 6. Звичайні дроби.
1.![]() Установити відповідність між звичайними дробами та їх характеристиками:
Установити відповідність між звичайними дробами та їх характеристиками:
-
 ; А. правильний дріб, менший за половину;
; А. правильний дріб, менший за половину;
-
 ; Б. неправильний дріб, більший за одиницю;
; Б. неправильний дріб, більший за одиницю;
-
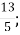 В. неправильний дріб, що дорівнює одному;
В. неправильний дріб, що дорівнює одному;
-
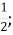 Г. мішане число; Д. правильний дріб, що дорівнює половині.
Г. мішане число; Д. правильний дріб, що дорівнює половині.
2.![]() Установити відповідність між звичайними дробами та їх характеристиками:
Установити відповідність між звичайними дробами та їх характеристиками:
-
 ; А. дріб, що менший за
; А. дріб, що менший за 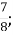
-
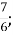 Б. дріб, що дорівнює 1;
Б. дріб, що дорівнює 1;
-
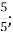 В. дріб, що дорівнює мішаному числу 1
В. дріб, що дорівнює мішаному числу 1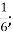
-
5
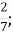 Г. дріб, що менший за
Г. дріб, що менший за  ; Д. число, що дорівнює дробу
; Д. число, що дорівнює дробу 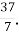
3.![]() Подати мішане число у вигляді неправильного дробу. Установити відповідність між мішаними числами та неправильними дробами:
Подати мішане число у вигляді неправильного дробу. Установити відповідність між мішаними числами та неправильними дробами:
-
6
 ; А.
; А. 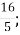
-
3
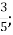 Б.
Б. 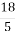 ;
;
-
7
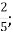 В.
В. 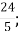
-
4
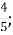 Г.
Г. 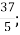 Д.
Д. 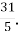
4.![]() Подати мішане число у вигляді неправильного дробу. Установити відповідність між мішаними числами та неправильними дробами:
Подати мішане число у вигляді неправильного дробу. Установити відповідність між мішаними числами та неправильними дробами:
-
8
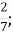 А.
А. 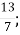
-
2
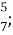 Б.
Б. 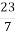 ;
;
-
1
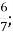 В.
В. 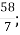
-
9
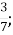 Г.
Г. 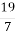 ; Д.
; Д. 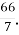
5.![]() Подати неправильний дріб у вигляді мішаного числа. Установити відповідність між неправильними дробами та мішаними числами:
Подати неправильний дріб у вигляді мішаного числа. Установити відповідність між неправильними дробами та мішаними числами:
-
 А. 3
А. 3 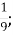
-
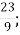 Б. 5
Б. 5 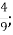
![]() В. 4
В. 4 ![]()
![]() Г. 2
Г. 2 ![]() Д. 1
Д. 1![]()
6.![]() Подати неправильний дріб у вигляді мішаного числа. Установити відповідність між неправильними дробами та мішаними числами:
Подати неправильний дріб у вигляді мішаного числа. Установити відповідність між неправильними дробами та мішаними числами:
-
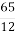 ; А. 1
; А. 1 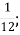
-
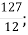 Б. 5
Б. 5 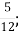
-
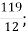 В. 10
В. 10 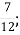
-
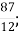 Г. 9
Г. 9 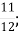 Д. 7
Д. 7 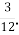
7.![]() Розв’язати задачі та встановити відповідність між задачами та відповідями до них:
Розв’язати задачі та встановити відповідність між задачами та відповідями до них:
-
У книзі 130 сторінок. Ігор прочитав
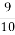 книги. Скільки сторінок залишилося прочитати Ігореві?
книги. Скільки сторінок залишилося прочитати Ігореві?
-
Сосна росте 450 років. Граничний вік верби становить
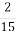 віку сосни. Скільки років росте верба?
віку сосни. Скільки років росте верба?
-
В автопарку 180 автомобілів. У рейс вийшло
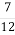 автомобілів. Скільки автомобілів вийшло у рейс?
автомобілів. Скільки автомобілів вийшло у рейс?
-
У класі 28 учнів. З них
 складають дівчата. Скільки хлопців у класі?
складають дівчата. Скільки хлопців у класі?
А. 12; Б. 105; В. 60; Г. 16; Д. 117.
8.![]() Розв’язати задачі і встановити відповідність між задачами і відповідями до них:
Розв’язати задачі і встановити відповідність між задачами і відповідями до них:
- Дівчинка зібрала 85 грибів, 32 з яких були білими, останні – лисичками. Яку частину всіх грибів становили лисички?
- У книзі 150 сторінок. Наталя прочитала 47 сторінок. Яку частину книги їй залишилося прочитати?
-
Прямий кут променем розбито на два кути. Один з них дорівнює 49
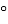 . Яку частину від прямого кута становить інший?
. Яку частину від прямого кута становить інший?
- Відрізок АВ точкою С поділено на дві частини. АВ = 45 см, АС = 18 см. Яку частину відрізка АВ становить відрізок ВС?
А. ![]() ; Г.
; Г. ![]() Є.
Є. ![]()
Б. ![]() ; Д.
; Д. ![]() Ж.
Ж. ![]()
В. ![]() ; Е.
; Е. ![]() ; З.
; З. ![]()
9.![]() Розв’язати задачі. Установити відповідність між задачами та відповідями до них:
Розв’язати задачі. Установити відповідність між задачами та відповідями до них:
-
Турист пройшов
 маршруту. Яка довжина маршруту, якщо він пройшов 4 км?
маршруту. Яка довжина маршруту, якщо він пройшов 4 км?
-
Велосипедист проїхав
 дороги. Скільки кілометрів залишилося проїхати велосипедисту, якщо він проїхав 45 км?
дороги. Скільки кілометрів залишилося проїхати велосипедисту, якщо він проїхав 45 км?
-
Морквою засіяли 28 га, що становить
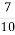 усієї площі поля, а цибулею засадили
усієї площі поля, а цибулею засадили  усієї площі поля. Скільки гектарів засадили цибулею?
усієї площі поля. Скільки гектарів засадили цибулею?
-
Мати зліпила вареники з сиром, Миколка пообідав 9-ма варениками, що становило
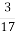 усіх вареників. Скільки вареників зліпила мати?
усіх вареників. Скільки вареників зліпила мати?
А. 15; Б. 27; В. 6; Г. 51; Д. 72.
10.![]() Знайти натуральне число х, для якого є правильною нерівність. Установити відповідність між нерівністю та значенням числа х:
Знайти натуральне число х, для якого є правильною нерівність. Установити відповідність між нерівністю та значенням числа х:
-
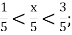 А. 14;
А. 14;
-
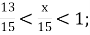 Б. 10;
Б. 10;
-
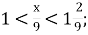 В. 24;
В. 24;
-
3
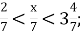 Г. 3; Д. 2.
Г. 3; Д. 2.
Тема 7. Додавання та віднімання звичайних дробів з однаковими знаменниками.
1.![]() Установити відповідність між виразами та їх значеннями:
Установити відповідність між виразами та їх значеннями:
-
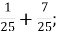 А.
А.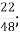
-
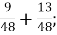 Б.
Б.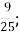
-
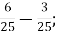 В.
В.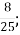
-
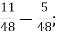 Г.
Г.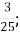 Д.
Д. 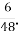
2.![]() Виконати дії і встановити відповідність між виразами та їх значеннями:
Виконати дії і встановити відповідність між виразами та їх значеннями:
-
2
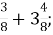 А. 2
А. 2 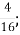
-
3
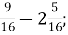 Б. 5
Б. 5 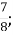
-
1
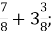 В. 1
В. 1 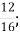
-
4
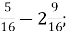 Г. 1
Г. 1 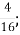 Д. 5
Д. 5  .
.
3.![]() Виконати дії і встановити відповідність між виразами та їх значеннями:
Виконати дії і встановити відповідність між виразами та їх значеннями:
-
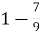 ; А. 1
; А. 1  ;
;
-
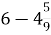 ; Б. 4
; Б. 4  ;
;
-
5
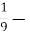
 ; В. 1
; В. 1  ;
;
-
7
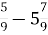 ; Г. 2
; Г. 2  ; Д.
; Д.  .
.
4.![]() Розв’язати рівняння і встановити відповідність між рівняннями та їх коренями:
Розв’язати рівняння і встановити відповідність між рівняннями та їх коренями:
-
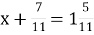 ; А.
; А.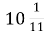 ;
;
-
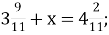 Б.
Б. 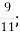
-
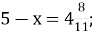 В.
В.  ;
;
-
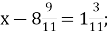 Г.
Г. 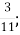 Д.
Д. 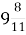 .
.
5. ![]() Розв’язати рівняння і встановити відповідність між рівняннями та їх коренями:
Розв’язати рівняння і встановити відповідність між рівняннями та їх коренями:
-
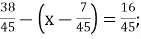 А.
А. 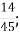
-
1
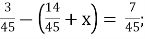 Б.
Б. 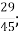
-
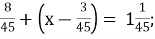 В. 1
В. 1 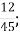
-
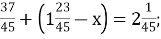 Г.
Г.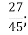 Д.
Д. 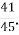
6.![]() Розв’язати рівняння і встановити відповідність між рівняннями та їх коренями:
Розв’язати рівняння і встановити відповідність між рівняннями та їх коренями:
-
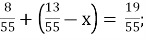 А. 13
А. 13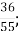 Д.
Д. 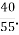
-
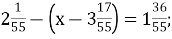 Б.
Б. 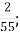
-
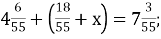 В. 3
В. 3 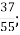
-
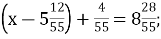 Г. 2
Г. 2 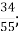
7.![]() Розв’язати задачі і встановити відповідність між задачами та відповідями до них:
Розв’язати задачі і встановити відповідність між задачами та відповідями до них:
-
Маса товару з упаковкою (брутто) -
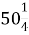 кг. Маса упаковки (тари) -
кг. Маса упаковки (тари) - 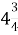 кг. Знайдіть масу товару.
кг. Знайдіть масу товару.
-
Першого дня до магазину привезли
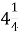 т овочів, а другого – 3
т овочів, а другого – 3 т. На скільки тон більше привезли овочів першого дня?
т. На скільки тон більше привезли овочів першого дня?
-
На базу привезли яблука на двох вантажівках. На першій було 4
 т яблук, а на другій – на 1
т яблук, а на другій – на 1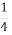 т менше. Скільки тонн яблук привезли на базу?
т менше. Скільки тонн яблук привезли на базу?
-
Довжина прямокутника 1
 м, а ширина – на
м, а ширина – на  м менша. Знайдіть периметр прямокутника.
м менша. Знайдіть периметр прямокутника.
А. 45![]() ; Б. 3
; Б. 3![]() ; В. 5
; В. 5![]() ; Г. 1
; Г. 1![]() ; Д.
; Д. ![]()
8.![]() Розв’язати задачі і встановити відповідність між задачами та відповідями до них:
Розв’язати задачі і встановити відповідність між задачами та відповідями до них:
-
За перший день продали 1
 т картоплі, що на
т картоплі, що на  т менше, ніж за другий день. Скільки тонн картоплі продали за два дні?
т менше, ніж за другий день. Скільки тонн картоплі продали за два дні?
-
Сторона квадрата 2
 см. Знайдіть його периметр.
см. Знайдіть його периметр.
-
За перший день туристи пройшли 15
 км, що на 3
км, що на 3 км більше, ніж за другий день. Скільки кілометрів пройшли туристи за два дні разом?
км більше, ніж за другий день. Скільки кілометрів пройшли туристи за два дні разом?
-
На новорічне свято купили 3
 кг цукерок і 2
кг цукерок і 2 кг апельсинів. Печива ж купили стільки, скільки цукерок та апельсинів разом. Скільки кілограмів становить вся покупка?
кг апельсинів. Печива ж купили стільки, скільки цукерок та апельсинів разом. Скільки кілограмів становить вся покупка?
А. 10![]() ; Б. 26
; Б. 26![]() ; В. 11
; В. 11![]() ; Г. 5
; Г. 5![]() ; Д. 2
; Д. 2![]() .
.
9.![]() Виконати дії зручним способом і встановити відповідність між прикладами та відповідями до них:
Виконати дії зручним способом і встановити відповідність між прикладами та відповідями до них:
-
(2
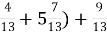 ; А. 6
; А. 6 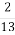 ;
;
-
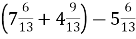 ; Б.
; Б. 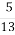 ;
;
-
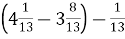 ; В. 8
; В. 8 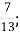
-
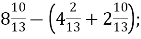 Г. 6
Г. 6 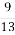 ; Д. 1
; Д. 1 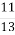 .
.
10.![]() Виконати дії зручним способом і встановити відповідність між прикладами та відповідями до них:
Виконати дії зручним способом і встановити відповідність між прикладами та відповідями до них:
-
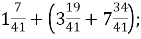 А. 1
А. 1 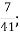
-
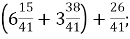 Б. 12
Б. 12 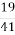 ;
;
-
1
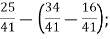 В.
В. 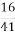 ;
;
-
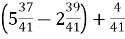 ; Г. 9
; Г. 9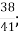 Д. 3
Д. 3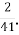
Тема 8. Поняття про десятковий дріб. Порівняння, округлення, додавання і віднімання десяткових дробів.
1.![]() Записати звичайний дріб у вигляді десяткового. Установити відповідність між звичайними дробами та десятковими:
Записати звичайний дріб у вигляді десяткового. Установити відповідність між звичайними дробами та десятковими:
-
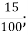 А. 0,015;
А. 0,015;
-
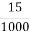 ; Б. 1,5;
; Б. 1,5;
-
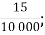 В. 0,15;
В. 0,15;
-
1
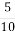 ; Г. 0,00015; Д. 0,0015.
; Г. 0,00015; Д. 0,0015.
2.![]() Записати звичайний дріб у вигляді десяткового. Установити відповідність між звичайними дробами та десятковими:
Записати звичайний дріб у вигляді десяткового. Установити відповідність між звичайними дробами та десятковими:
-
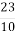 ; А. 0,23;
; А. 0,23;
-
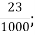 Б. 0,023;
Б. 0,023;
-
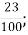 В. 2,3;
В. 2,3;
-
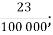 Г.
Г.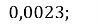 Д. 0,00023.
Д. 0,00023.
3.![]() Округлити число до вказаного розряду. Установити відповідність між числом та його наближенням:
Округлити число до вказаного розряду. Установити відповідність між числом та його наближенням:
- 0,327 до сотих; А. 0,3;
- 0,0327 до тисячних; Б. 0,32;
- 3,27 до десятих; В. 0,033;
- 0,327 до десятих; Г. 3,3; Д. 0,33.
4.![]() Округлити число до вказаного розряду. Установи відповідність між числом та його наближенням:
Округлити число до вказаного розряду. Установи відповідність між числом та його наближенням:
- 9,1583 до сотих; А. 9,1;
- 9,1583 до тисячних; Б. 9,2;
- 9,1583 до десятих; В. 9,158;
- 91,583 до одиниць; Г. 9,16; Д. 92.
5.![]() Знайти число т, для якого нерівність вірна. Установити відповідність між нерівностями та числами:
Знайти число т, для якого нерівність вірна. Установити відповідність між нерівностями та числами:
-
0,4
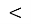 т
т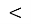 0,6; А. т = 2,375;
0,6; А. т = 2,375;
-
2,37
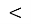 т
т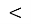 2,39; Б. т = 17,87;
2,39; Б. т = 17,87;
-
17,8
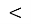 т
т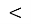 17,9; В. т = 32,94;
17,9; В. т = 32,94;
-
32,9
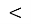 т
т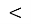 33; Г. т = 0,5; Д. т = 2,4.
33; Г. т = 0,5; Д. т = 2,4.
6.![]() Знайти число т, для якого нерівність вірна. Установити відповідність між нерівностями та числами:
Знайти число т, для якого нерівність вірна. Установити відповідність між нерівностями та числами:
-
38,4
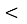 т
т 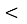 38,42; А. 6,28;
38,42; А. 6,28;
-
4,97
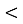 т
т 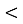 4,98; Б. 521,09;
4,98; Б. 521,09;
-
521,08
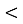 т
т 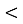 521,1; В. 6,301;
521,1; В. 6,301;
-
6,25
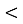 т
т 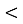 6,3; Г. 38,41; Д. 4,975.
6,3; Г. 38,41; Д. 4,975.
7.![]() Додати десяткові дроби. Установити відповідність між прикладами та відповідями до них:
Додати десяткові дроби. Установити відповідність між прикладами та відповідями до них:
- 7,8 + 6,9; А. 96,381;
- 24,2 + 0,876; Б. 160,376;
- 96,3 + 0,081; В. 159,466;
- 50,096 + 109,37; Г. 25,076; Д. 14,7.
8.![]() Відняти десяткові дроби. Установити відповідність між прикладами та відповідями до них:
Відняти десяткові дроби. Установити відповідність між прикладами та відповідями до них:
- 20,85 – 6,149; А. 6,057;
- 0,05 – 0,0069; Б. 14,701;
- 254 – 3,097; В. 0,431;
- 25,6 – 19,543; Г. 19,287; Д. 250,903.
9.![]() Розв’язати задачі і встановити відповідність між задачами та відповідями до них:
Розв’язати задачі і встановити відповідність між задачами та відповідями до них:
- Швидкість катера за течією річки дорівнює 19,6 км/год., а власна швидкість катера – 18,3 км/год. Знайти швидкість катера проти течії річки.
- Швидкість моторного човна проти течії річки дорівнює 17,8 км/год., а власна швидкість човна – 19,4 км/год. Знайти швидкість моторного човна за течією річки.
- Швидкість теплохода в стоячій воді 38, 2 км/год., а швидкість течії річки – 1,8 км/год. Знайти швидкість теплохода проти течії річки.
- З однієї ділянки зібрали 27,3 т зерна, що на 12,8 т більше, ніж з другої ділянки. Скільки тон зерна зібрали з обох ділянок?
А. 41,8; Б. 36,4; В. 21; Г. 17; Д. 20,9
10.![]() Розв’язати задачі і встановити відповідність між задачами та відповідями до них:
Розв’язати задачі і встановити відповідність між задачами та відповідями до них:
- Довжина бічної сторони рівнобедреного трикутника дорівнює 10,1 см, а довжина основи на 0,3 см менша. Знайти периметр трикутника.
- Маса трьох кавунів 25,67 кг, маса одного з них – 6,87 кг, а маса другого – на 1,55 кг більша. Знайти масу третього кавуна.
- Одна з сторін прямокутника дорівнює 5,7 см, що на 1,9 см більше за іншу. Знайти периметр прямокутника.
- За перший день робітники відремонтували 8,9 км дороги, а за другий день – на 1,92 км менше, ніж за перший. Після цього їм залишилось відремонтувати ще 5,97 км дороги. Скільки кілометрів дороги треба було відремонтувати?
А. 21,85; Б. 19; В. 10,38; Г. 30; Д. 26,6.
11.![]() Розв’язати рівняння і встановити відповідність між рівняннями та їх коренями:
Розв’язати рівняння і встановити відповідність між рівняннями та їх коренями:
- (51,7 – х) + 3,4 = 12,6; А. 7,26;
- (х – 32,6) + 5,9 = 16, 7; Б. 19,72;
- 20,54 – (х – 13,27) = 14,09; В. 43,4;
- (х + 17,8) – 23,07 =1,99; Г. 47,9;
Д. 42,5.
12. ![]() Розв’язати рівняння і встановити відповідність між рівняннями та їх коренями:
Розв’язати рівняння і встановити відповідність між рівняннями та їх коренями:
- (72,9 – х) + 3,1 = 15,6; А. 43,59;
- (х – 34,8) + 2,5 = 11,29; Б. 26,94;
- 35,07 – (х – 8,4) = 16,53; В. 64,88;
- (х + 14,3) – 37,2 = 41,98; Г. 19,08; Д. 60,4.
Тема 9. Множення та ділення десяткових дробів.
1.![]() Знайдіть добуток чисел. Установіть відповідність між виразами та їх значеннями:
Знайдіть добуток чисел. Установіть відповідність між виразами та їх значеннями:
-
3,6
 0,78; А. 4,6585;
0,78; А. 4,6585;
-
5,1
 23,9; Б. 2,0301;
23,9; Б. 2,0301;
-
2,01
 1,01; В. 46,585;
1,01; В. 46,585;
-
6,05
 0,77. Г.121,89; Д. 2,808.
0,77. Г.121,89; Д. 2,808.
2.![]() Знайдіть добуток чисел. Установіть відповідність між виразами та їх значеннями:
Знайдіть добуток чисел. Установіть відповідність між виразами та їх значеннями:
-
4,5
 0,97; А. 6,2128;
0,97; А. 6,2128;
-
6,3
 18,9; Б. 4,365;
18,9; Б. 4,365;
-
3,02
 2,01; В. 607,02;
2,01; В. 607,02;
-
7,06
 0,88. Г. 119,07; Д. 6,0702.
0,88. Г. 119,07; Д. 6,0702.
3.![]() Дано сторони прямокутника а та в. Знайти його площу S. Установити відповідність між сторонами та площею прямокутника:
Дано сторони прямокутника а та в. Знайти його площу S. Установити відповідність між сторонами та площею прямокутника:
-
а = 2,6 м; в = 0,4 м; А. S = 0,008
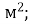
-
а = 36,5 м; в = 0,7 м; Б. S = 2,555
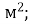
-
а = 6,08 м; в = 2,3 м; В. S = 1,04
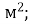
-
а = 0,08 м; в = 0,1м; Г. S = 25,55
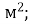 Д. S = 13,984
Д. S = 13,984 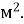
4.![]() Турист рухався t годин зі швидкістю v км/год. Знайти шлях s, пройдений туристом і встановити відповідність:
Турист рухався t годин зі швидкістю v км/год. Знайти шлях s, пройдений туристом і встановити відповідність:
- t = 3,5 год.; v = 4,9 км/год. А. s = 14,85 км;
- t = 5,4 год.; v = 5,3 км/год. Б. s = 171,5 км;
- t = 2,7 год.; v = 5,5 км/год. В. s = 28,62 км;
- t = 6 год.; v = 4,5 км/год. Г. s = 17,15 км;
Д. s = 27 км.
5.![]() Знайти значення виразу 2,5х + 3,7у при заданих значеннях х та у. Установити відповідність між виразом та його значенням:
Знайти значення виразу 2,5х + 3,7у при заданих значеннях х та у. Установити відповідність між виразом та його значенням:
- х = 10, у = 0,1; А. 250,037;
- х = 0,1, у = 10; Б. 25,37;
- х = 100, у = 0,01; В. 370,025;
- х = 0,01, у = 100. Г. 37,25; Д. 25,037.
6. Розв’язати задачі і встановити відповідність між задачами та відповідями до них:
-
 Товарний і пасажирський потяги вийшли з одного пункту в протилежних напрямках. Швидкість товарного потягу дорівнює 42 км/год., а швидкість пасажирського – 74 км/год. Зараз між ними відстань 20,6 км. Яка відстань буде між ними через 0,4 години?
Товарний і пасажирський потяги вийшли з одного пункту в протилежних напрямках. Швидкість товарного потягу дорівнює 42 км/год., а швидкість пасажирського – 74 км/год. Зараз між ними відстань 20,6 км. Яка відстань буде між ними через 0,4 години?
-
 Знайти об’єм коробки, що має форму прямокутного паралелепіпеда, ширина якого дорівнює 2,5 дм, висота – у 0,8 рази більша за ширину, а довжина – в 1,8 рази більша за висоту.
Знайти об’єм коробки, що має форму прямокутного паралелепіпеда, ширина якого дорівнює 2,5 дм, висота – у 0,8 рази більша за ширину, а довжина – в 1,8 рази більша за висоту.
-
 Катер рухався 2 год. за течією і 3 год. проти течії. Який шлях подолав за цей час катер, якщо швидкість течії дорівнює 2,2 км/год., а власна швидкість катера – 11,3 км/год.?
Катер рухався 2 год. за течією і 3 год. проти течії. Який шлях подолав за цей час катер, якщо швидкість течії дорівнює 2,2 км/год., а власна швидкість катера – 11,3 км/год.?
-
 З двох міст назустріч один одному одночасно вирушили велосипедист і мотоцикліст. Швидкість велосипедиста дорівнює 12,8 км/год., а швидкість мотоцикліста в 4 рази більша, ніж швидкість велосипедиста. Вони зустрілися через 2,2 год. Знайти відстань між містами.
З двох міст назустріч один одному одночасно вирушили велосипедист і мотоцикліст. Швидкість велосипедиста дорівнює 12,8 км/год., а швидкість мотоцикліста в 4 рази більша, ніж швидкість велосипедиста. Вони зустрілися через 2,2 год. Знайти відстань між містами.
А. 112,64; Б. 67; В. 18; Г. 54,3; Д. 140,8.
7.![]() Виконати ділення на натуральне число. Установити відповідність між прикладами та відповідями до них:
Виконати ділення на натуральне число. Установити відповідність між прикладами та відповідями до них:
- 118,95: 5; А. 0,36;
- 25,656 : 8; Б. 3,6;
- 25,56 : 71; В. 0,026;
- 0,806 : 31; Г. 3,207;
Д. 3,79.
8.![]() Виконати ділення на натуральне число. Установити відповідність між прикладами та відповідями до них:
Виконати ділення на натуральне число. Установити відповідність між прикладами та відповідями до них:
- 24,48 : 12; А. 2,553;
- 35,742 : 14; Б. 0,002;
- 25,036 : 44; В. 0,0005;
- 0,023 : 46. Г. 2,04; Д. 0,569.
9.![]() Виконати ділення на розрядну одиницю. Установити відповідність між прикладами та відповідями до них:
Виконати ділення на розрядну одиницю. Установити відповідність між прикладами та відповідями до них:
- 56,009 : 10; А. 560 090;
- 560,09 : 100; Б. 560,09;
- 5,6009 : 1000; В. 56 009;
- 5600,9 : 100; Г. 5,6009; Д. 5 600,9.
10.![]() Виконати ділення на розрядну одиницю. Установити відповідність між прикладами та відповідями до них:
Виконати ділення на розрядну одиницю. Установити відповідність між прикладами та відповідями до них:
- 76,04 : 10; А. 7 604;
- 7,604 : 100; Б. 76,04;
- 7,604 : 1000; В. 7,604;
- 7 604 : 100; Г. 0,007604; Д. 0,07604.
11.![]() Виконати ділення на десятковий дріб. Установити відповідність між прикладами та відповідями до них:
Виконати ділення на десятковий дріб. Установити відповідність між прикладами та відповідями до них:
- 12,5 : 0,125; А. 81,4;
- 11,89 : 2,9; Б. 120;
- 13,08 : 0,109; В. 4,1;
- 6,105 : 0,075; Г. 8,14; Д. 100.
12.![]() Виконати ділення на десятковий дріб. Установити відповідність між прикладами та відповідями до них:
Виконати ділення на десятковий дріб. Установити відповідність між прикладами та відповідями до них:
- 0,308 : 0,14; А. 12,225;
- 7,95 : 1,5; Б. 2,2;
- 19,56 : 0,016; В. 5,3;
- 169,2 : 0,423; Г. 122,25; Д. 400.
13.![]() Розв’язати рівняння. Установити відповідність між рівняннями та їх коренями:
Розв’язати рівняння. Установити відповідність між рівняннями та їх коренями:
- 5х + 4,3 =8,05; А. 0,14;
- 10х – 3,06 = 12,78; Б. 0,75;
-
4,5
 (10х + 5,5) = 90; В. 15,84;
(10х + 5,5) = 90; В. 15,84;
- 10 : (18 – 100х) = 2,5; Г. 1,584; Д. 1,45.
14.![]() Розв’язати рівняння. Установити відповідність між рівняннями та їх коренями:
Розв’язати рівняння. Установити відповідність між рівняннями та їх коренями:
- 4х + 7,8 =13,07; А. 1,754;
- 10х – 4,09 = 25,98; Б. 0,51;
- 5,6 : (10х – 4,6) = 11,2; В. 0,3;
- 100 :(38 – 100х) = 12,5; Г. 3,007; Д. 17,54.
15. Розв’язати задачі. Установити відповідність між задачами та відповідями до них:
-
 Мотоцикліст проїхав 161,5 км за 3,8 години. Знайдіть швидкість мотоцикліста.
Мотоцикліст проїхав 161,5 км за 3,8 години. Знайдіть швидкість мотоцикліста.
-
 З поля площею 3,2 га зібрали 81,6 ц зерна. Яка врожайність зерна на цьому полі?
З поля площею 3,2 га зібрали 81,6 ц зерна. Яка врожайність зерна на цьому полі?
-
 Під час посіву гречки на 0,24 га витратили 0,03 т зерна. Скільки тонн зерна потрібно, щоб засіяти площу у 7,5 га?
Під час посіву гречки на 0,24 га витратили 0,03 т зерна. Скільки тонн зерна потрібно, щоб засіяти площу у 7,5 га?
-
 Маса 0,3
Маса 0,3 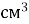 алюмінію дорівнює 0,81 г. Знайдіть масу 1
алюмінію дорівнює 0,81 г. Знайдіть масу 1 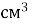 алюмінію.
алюмінію.
А. 2,7; Б. 0,9375; В. 25,5; Г. 42,5; Д. 93,75.
16. Розв’язати задачі. Установити відповідність між задачами та відповідями до них:
-
 Гусениця проповзла 6,16 м за 2,2 хв., а равлик – 6,48 м за 3,6 хв. На скільки м/хв. швидкість гусениці більша за швидкість равлика?
Гусениця проповзла 6,16 м за 2,2 хв., а равлик – 6,48 м за 3,6 хв. На скільки м/хв. швидкість гусениці більша за швидкість равлика?
-
 Пасажирський потяг іде слідом за товарним. Швидкість пасажирського потягу дорівнює 64,3 км/год., а швидкість товарного – 42,7 км/год. Зараз між ними 14,88 км. Яка відстань була між потягами 0,7 год. тому?
Пасажирський потяг іде слідом за товарним. Швидкість пасажирського потягу дорівнює 64,3 км/год., а швидкість товарного – 42,7 км/год. Зараз між ними 14,88 км. Яка відстань була між потягами 0,7 год. тому?
-
 Машина подолала 270 км. Перші 96 км вона проїхала за 1,5 год., а решту їхала зі швидкістю 72,5 км/год. За який час машина подолала всю відстань?
Машина подолала 270 км. Перші 96 км вона проїхала за 1,5 год., а решту їхала зі швидкістю 72,5 км/год. За який час машина подолала всю відстань?
-
 Бічна сторона рівнобедреного трикутника дорівнює 5,2 см, що становить 0,8 основи. Знайдіть периметр трикутника.
Бічна сторона рівнобедреного трикутника дорівнює 5,2 см, що становить 0,8 основи. Знайдіть периметр трикутника.
А. 16,9; Б. 3,9; В. 1; Г. 4,6; Д. 30.
Тема 10. Відсотки. Середнє арифметичне.
1.![]() Знайти відсоток від числа. Установити відповідність між завданням та відповіддю:
Знайти відсоток від числа. Установити відповідність між завданням та відповіддю:
- 12% від 45; А. 54;
- 1,2% від 45; Б. 0,54;
- 120% від 45; В. 540;
- 12% від 0,45; Г. 0,0054; Д. 5,4.
2.![]() Знайти відсоток від числа. Установити відповідність між завданням та відповіддю:
Знайти відсоток від числа. Установити відповідність між завданням та відповіддю:
- 18% від 35; А. 0,63;
- 1,8% від 0,35; Б. 0,0063;
- 180% від 35; В. 63;
- 0,18% від 350; Г. 0,063; Д. 6,3.
3.![]() Знайти число за його відсотком. Установити відповідність між завданням та відповіддю:
Знайти число за його відсотком. Установити відповідність між завданням та відповіддю:
- 6% - це 96; А. 16;
- 60% - це 9600; Б. 1 600;
- 0,6% - це 960; В. 160 000;
- 6% - це 0,96; Г. 160; Д. 16 000.
4.![]() Знайти число за його відсотком. Установити відповідність між завданням та відповіддю:
Знайти число за його відсотком. Установити відповідність між завданням та відповіддю:
- 50% - це 75; А. 1,5;
- 5% - це 0,75; Б. 150;
- 0,05% - це 0,075; В. 15;
- 5% - це 750; Г. 0,15; Д. 15 000.
5.![]() Знайти середнє арифметичне чисел. Установити відповідність між числами та їх середнім арифметичним:
Знайти середнє арифметичне чисел. Установити відповідність між числами та їх середнім арифметичним:
- 2,4 і 6,8; А. 38,2;
- 12,9 і 63,5; Б. 52,5;
- 27,3; 35,1 і 42,6; В. 46,2;
- 47,1; 43,2; 48,9 і 45,6; Г. 4,6; Д. 35.
6.![]() Знайти середнє арифметичне чисел. Установити відповідність між числами та їх середнім арифметичним:
Знайти середнє арифметичне чисел. Установити відповідність між числами та їх середнім арифметичним:
-
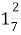 і
і 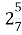 ; А.
; А.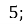
-
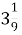 і 6
і 6 ; Б.
; Б.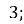
-
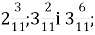 В.
В.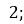
-
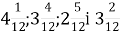 ; Г.
; Г. 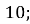 Д.
Д. 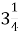 .
.
7. Розв’язати задачі. Установити відповідність між умовами задач та відповідями до них:
-
 До магазину привезли 850 кг огірків. Іван Іванович купив 3% всіх огірків. Скільки кілограмів огірків купив Іван Іванович?
До магазину привезли 850 кг огірків. Іван Іванович купив 3% всіх огірків. Скільки кілограмів огірків купив Іван Іванович?
-
 У книзі 500 сторінок. Дівчинка прочитала 7% усієї книги. Скільки сторінок прочитала дівчинка?
У книзі 500 сторінок. Дівчинка прочитала 7% усієї книги. Скільки сторінок прочитала дівчинка?
-
 На складі було 360 т вугілля. Згодом вивезли 25% всього вугілля. Скільки тонн вугілля залишилось на складі?
На складі було 360 т вугілля. Згодом вивезли 25% всього вугілля. Скільки тонн вугілля залишилось на складі?
-
 У саду росте 250 яблунь ранніх, середніх та пізніх сортів. З них ранніх сортів – 70%, пізніх – 14%, останні яблуні середніх сортів. Скільки яблунь середніх сортів росте у саду?
У саду росте 250 яблунь ранніх, середніх та пізніх сортів. З них ранніх сортів – 70%, пізніх – 14%, останні яблуні середніх сортів. Скільки яблунь середніх сортів росте у саду?
А. 90; Б. 25,5; В. 40; Г. 255; Д. 35.
8. Розв’язати задачі. Установити відповідність між умовами задач та відповідями до них:
-
 Прилад вартістю 3 000 грн. подешевшав на 29%. На скільки гривень подешевшав прилад?
Прилад вартістю 3 000 грн. подешевшав на 29%. На скільки гривень подешевшав прилад?
-
 В місті раніше проживало 4млн жителів. За останні 10 років кількість населення виросла на 17%. Скільки жителів проживає у цьому місті зараз?
В місті раніше проживало 4млн жителів. За останні 10 років кількість населення виросла на 17%. Скільки жителів проживає у цьому місті зараз?
-
 Банківський внесок у 30 000 грн. за рік збільшився на 6%. Скільки гривень стало на рахунку через рік?
Банківський внесок у 30 000 грн. за рік збільшився на 6%. Скільки гривень стало на рахунку через рік?
-
 Потрібно було відремонтувати 140 км дороги. За перший місяць відремонтували 36%, за другий – 50% того, що залишилось, за третій місяць ремонт дороги був завершений. Скільки кілометрів дороги відремонтували за третій місяць?
Потрібно було відремонтувати 140 км дороги. За перший місяць відремонтували 36%, за другий – 50% того, що залишилось, за третій місяць ремонт дороги був завершений. Скільки кілометрів дороги відремонтували за третій місяць?
А. 34 800; Б. 4 680 000; В. 870; Г. 2 130; Д. 44,8.
9. Скласти рівняння за умовою задачі. Знайти невідоме число. Установити відповідність між умовою задачі та шуканим числом:
-
 Середнє арифметичне двох чисел дорівнює 12,3. Одне з них дорівнює 11,9. Знайти друге число.
Середнє арифметичне двох чисел дорівнює 12,3. Одне з них дорівнює 11,9. Знайти друге число.
-
 Середнє арифметичне трьох чисел дорівнює 65,13. Перше число дорівнює другому, а третє – на 5,1 більше. Знайти третє число.
Середнє арифметичне трьох чисел дорівнює 65,13. Перше число дорівнює другому, а третє – на 5,1 більше. Знайти третє число.
-
 Велосипедист їхав 2 год. зі швидкістю 12,6 км/год. і 4 год. зі швидкістю 13,5 км/год. Знайти середню швидкість велосипедиста на всьому шляху.
Велосипедист їхав 2 год. зі швидкістю 12,6 км/год. і 4 год. зі швидкістю 13,5 км/год. Знайти середню швидкість велосипедиста на всьому шляху.
-
 Автомобіль проїхав першу частину шляху за1,8 год. зі швидкістю 68 км/год., а другу частину – за 2,2 год. З якою швидкістю проїхав автомобіль другу частину шляху, якщо середня швидкість протягом усього шляху становила 75,7 км/год.?
Автомобіль проїхав першу частину шляху за1,8 год. зі швидкістю 68 км/год., а другу частину – за 2,2 год. З якою швидкістю проїхав автомобіль другу частину шляху, якщо середня швидкість протягом усього шляху становила 75,7 км/год.?
А. 82; Б. 13,2; В. 68,53; Г. 58,33; Д. 12,7.
10. Скласти рівняння за умовою задачі. Знайти невідоме число. Установити відповідність між умовою задачі та шуканим числом:
-
 Середнє арифметичне чисел а, в і с дорівнює 13,6. Знайти число а, якщо в + с = 26,6.
Середнє арифметичне чисел а, в і с дорівнює 13,6. Знайти число а, якщо в + с = 26,6.
-
 Середнє арифметичне декількох чисел дорівнює 15,5. Знайти кількість цих чисел, якщо їх сума дорівнює 77,5.
Середнє арифметичне декількох чисел дорівнює 15,5. Знайти кількість цих чисел, якщо їх сума дорівнює 77,5.
-
 Середнє арифметичне трьох чисел дорівнює 3,5. Друге число більше за перше у 2,5 рази, а третє число більше за друге на 0,6. Знайти перше число.
Середнє арифметичне трьох чисел дорівнює 3,5. Друге число більше за перше у 2,5 рази, а третє число більше за друге на 0,6. Знайти перше число.
-
 Середнє арифметичне трьох чисел дорівнює 15, а середнє арифметичне двох інших чисел дорівнює 10. Знайти середнє арифметичне цих п’яти чисел.
Середнє арифметичне трьох чисел дорівнює 15, а середнє арифметичне двох інших чисел дорівнює 10. Знайти середнє арифметичне цих п’яти чисел.
А. 13; Б. 1,65; В. 14,2; Г. 5; Д.16,5.
Література
- Тарасенкова Н. А.
Математика: підручник для 5 класу загальноосвітніх навчальних закладів. – К.: Видавничий дім «Освіта»,2018.
- Мерзляк А. Г.
Математика. 5 кл. : Збірник задач і контрольних робіт. – Х. : Гімназія, 2013.
- Мерзляк А. Г., Полонський В. Б., Якір М. С.
Математика. 5 клас. Книга для вчителя. – Х.: Гімназія, 2005.
- Бевз Г. П., Бевз В. Г.
Уроки математики в 5 класах. Посібник для вчителя. – К.: Педагогічна преса, 2006.
- Тарасенкова Н. А.
Зошит для контролю навчальних досягнень з математики. 5 клас.: Навч.-метод. посібник. – К. : Видавничий дім «Освіта», 2018.
- Старова О. О., Маркова І. С.
Математика. 5 клас (за підручником О. С. Істер) – Х. : Видавнича група «Основа», 2013. (Серія «Мій конспект»).


про публікацію авторської розробки
Додати розробку
