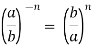Урок "Узагальнення поняття степеня "

Алгебра           10 клас

Тема уроку: Узагальнення поняття степеня

Мета уроку: формування поняття степеня з раціональним показником, степінь з ірраціональним показником

Хід уроку

1. Організаційний етап
2. Перевірка домашнього завдання

Відповіді на запитання, що виникли в учнів при розв’язуванні домашнього завдання.

3. Повторення і систематизація знань учнів про степінь з натуральним і цілим показником

Повторення і систематизацію знань учнів про степінь із натуральним і цілим показником рекомендується провести шляхом бесіди з використанням таблиці.

Питання до класу:

1. Що називається n-м степенем числа а, якщо n N? Якщо n = 1? n = 0?
2. Що таке степінь, основа степеня, показник степеня?
3. Що називається n-м степенем числа а, якщо n ?
4. Сформулюйте основні властивості степенів.

4. Формування поняття степеня з дробовим показником.

Введемо поняття степеня з дробовим показником. Вводячи це поняття, хотілося би, щоб степінь з раціональним показником мав ті самі властивості, що й степінь із цілим показником.

Зокрема, n-й степінь числа повинен дорівнювати a^m. Якщо ця властивість виконується, то , а це означає (за означенням кореня n-того степеня), що число повинно бути коренем n-того степеня із числа .

Степенем , числа а>0 з раціональним показником , де m , n N (n>1) називається число

Отже, .

Степінь числа 0 визначений тільки для додатних показників;

За означенням 0^r = 0 для будь-якого r>0.

Виконання вправ в парах

1. Подайте вирази у вигляді степеня з раціональним показником:

а) ; б) ; в) ; г)

Відповідь: а) ; б) ; в) ; г) .

2. Подайте вирази у вигляді кореня із числа чи виразу:

а) ; б) 2; в) ; г) 2

Відповідь: а) ; б) 2; в) ; г) .

3. Обчисліть:

а) ; б) ; в) ; г)

Відповідь: а) 9; б) 4; в) 4; г) 27.

5. Вивчення властивостей степенів з раціональним показником

Для будь-яких раціональних чисел р і q і будь-яких додатних а і справедливі рівності:

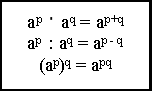
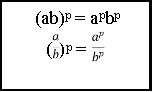
Для доведення цих властивостей треба скористатися означенням степеня з раціональним показником  властивостями коренів. Доведемо першу рівність: нехай , тоді a^p a^q = .

Останні рівності доводяться аналогічно.

Виконання вправ №429; №431.

6. Сприймання поняття про степінь з ірраціональним показником.

Розглянемо степінь з ірраціональним показником можна подати у вигляді нескінченного неперіодичного десяткового дробу.

Розглянемо послідовність наближень числа :

1< < 2,

1,4 < < 1,5,

1,41 < < 1,42,

1,414 < < 1,415,

1,4142 < < 1,4143,

…

За допомогою калькулятора знайдемо наближені значення степенів числа 10 з недостачею і надлишком, тоді матимемо:

10 = 10¹ < < 10² = 100

25,119 < < 10^1,5 31,623

25,704 10^1,41 < < 10^1,42 26,303

25,942 10^1,414 < < 10^1,415 26,002

25,963 10^1,4142 < < 10^1,4143 25,960

…

Наведені значення з недостачею і надлишком наближаються до одного і того самого числа = 25,9…, яке і прийнято вважати степенем числа 10 з показником .

Таким чином, ми розширили поняття степеня на будь-які дійсні показники, зберігаючи при цьому властивості степеня.

7. Підведення підсумків уроку

Бліц-опитування

8. Домашнє завдання. §3 п.15, №422, 424, 426, 430.

(А.Г.Мерзляк Алгебра і початки аналізу, 10 клас)