Урок "Вільні коливання в коливальному контурі"

П.М. Клініч, Солобковецький ЗЗСО , Ярмолинецький р-н, Хмельницька обл.

 

Фізика, 11 клас, Урок 42

Успіх у науці – справа часу та сміливості розуму

 (Вольтер).

Тема: Вільні коливання в коливальному контурі.

Мета : вивести формули енергії конденсатора та котушки, частоти та періоду коливань, формулу Томсона; розвивати експериментальні уміння вимірювати фізичні величини та спостерігати графіки коливань; виховувати спостережливість, повагу до експерименту.

Основні поняття: коливання, контур, котушка, конденсатор, осцилограф, генератор, калькулятор,

Обладнання: програма «Віртуальний осцилограф», генератор НЧ, котушка, конденсатор, діод, провідники, джерело струму, комп’ютер.

Тип уроку: пояснення нового матеріалу.

Хід уроку

І. Розминка.

Вправа «Пазли»

На двох комп’ютерах запущено дві однакові програми для складання пазлів, наприклад  NSG(Або дві однакові програми на одній мультимедійній дошці). Потрібно скласти електричне коло для сьогоднішньої роботи. Учні діляться на дві команди, по черзі підходять до комп’ютерів і, переміщаючи фрагменти, складають слово(«Осцилограма»). Команда, що виконала завдання першою, отримує бали.

На минулих уроках ми з вами вивчали механічні коливання. Було встановлено ряд цікавих якісних та кількісних закономірностей таких коливань. Зокрема:

• Механічні коливання поширюються в …  середовищах
• Між частотою та періодом коливань існує співвідношення …
• Для  математичного та фізичного маятників існують формули, які описують залежності періодів коливань від параметрів цих маятників…
• Спостерігали часову розгортку …  коливань за допомогою реального та віртуального осцилографів, використовуючи мікрофон та комп’ютер. (учні по черзі відповідають та доповнюють)

 

ІІІ. Мотивація навчальної діяльності

• Чи існують електричні коливання?
• Чим відрізняються електричні коливання від механічних?
• Якщо механічні коливання можна спостерігати, то яка ситуація з електромагнітними коливаннями?
• Чи існують способи спостерігати за електричними коливаннями?
• Від чого залежать параметри електричних коливань?
• Де використовуються електричні коливання?

 

План-схема уроку 42

Етап уроку	Час, хв	Форма і методи діяльності вчителя	Результат
І.Розминка	3	Гра «Пазли»	Створення сприятливого психоемоційного клімату
ІІ. Актуалізація опорних знань	5	Бесіда	Активізація пізнавальної діяльності
ІІІ. Мотивація навчальної діяльності	2	Постановка проблемних запитань групах.	Мотивація навчальної діяльності
IV. Пояснення нового матеріалу	23	Бесіда. Фронтальний експеримент	Усвідомлення нового матеріалу
V.Корекція знань учнів	5	Інтерактивна вправа «Продовж  думку».	Виявлення хибних уявлень учнів
VI. Підсумки уроку	5	Міні-виступ «Що я сьогодні відкрив для себе?»	Підбиття підсумків уроку
VII. Домашнє завдання	2	Репродуктивного характеру. Розв’язування вправи

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

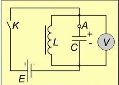Найпростішим пристроєм, 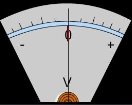в якому досить просто можна спостеріга­ти електромагнітні коливання, є електричне коло, що складається з котушки індуктивністю L, та конденсатора ємністю С . Зрозуміло, що провідник, з якого виготовлено котушку, має й активний опір R, але спочатку ми ним нехтуватимемо. Щоб легко можна було спостерігати за змінами напруги на обкладинках конденсатора, до яких під'єднано вольтметр V, коливання мають бути досить повільні. Тому в такому пристрої використовують котушку значної індуктивності (на­приклад 25 Гн) і конденсатор великої ємності (1000-2000 мкФ). Вольтметр беруть з нульовою поділкою посередині шкали. Коли замкнути ключ К, то конденсатор С зарядиться від джерела постійного струму Е і вольтметр покаже напругу на його обкладинках. Від'єднуємо джерело від досліджуваного кола. Вольтметр покаже наявність коливань напруги, які швидко припиняються. Значення і знак напруги на обкладинках конденсатора змінюються, що засвідчує періодичне перезаряджання обкладинок конденсатора.

Отже, можна дійти висновку, що коли систему вивести зі стану рівноваги (зарядити конденсатор від стороннього джерела), то після від'єднання джерела в колі відбуватимуться коливання напру и і пов'язаного з напругою простим співвідношенням заряду q=CU (1). Проте оскільки напруга є енергетичною характеристикою електричного поля, й енергію електричного поля конденса­тора визначають за формулою (2), то зі зміною напруги відбуваються також періодичні зміни енергії електричного поля конденсатора (аналогічно змінам потенціальної енергії пружини у разі виникнення гармонічних коливань тягар на пружині).

На який же інший вид енергії перетворюється енергія електричного поля конденсатора? Під час перезарядження обкладинок конденсатора в котушці виникає струм, сила якого визначає енергію магнітного поля котушки:   (3).

 

 

Щоб упевнитись у правильності зробленого нами висновку про перетворення енергії, в точку А досліджуваного електричного кола треба помістити амперметр, також з нульовою поділкою посередині шкали. Вимірювальні прилади покажуть, що коли на­пруга на обкладинках конденсатора максимальна, то сила струму в колі дорівнює нулю, і навпаки, коли напруга дорівнює нулю, то си­ла струму максимальна. Отже, можна говорити про періодичні пе­ретворення енергії електричного поля конденсатора на енергію ма­гнітного поля котушки зі струмом і навпаки.

Досліджувані коливання швидко припиняються, що зумовлено витратами енергії на нагрі­вання провідників, перемагнічування феромагнітного осердя котушки, випромінювання частини енергії в простір у вигляді електромагнітних хвиль. Лише в ідеальному випадку, коли б не було втрат енергії в коливальному контурі, максимальна енергія електричного поля конденсатора дорівнювала б максимальній енергії магнітного поля котушки зі струмом: (4). У цьому разі справджувався б закон збереження електромагнітної енергії, і в будь-який момент часу сума енергій електричного і магнітного полів залишалася б сталою (5), де U і I - миттєві значення напруги і сили струму.

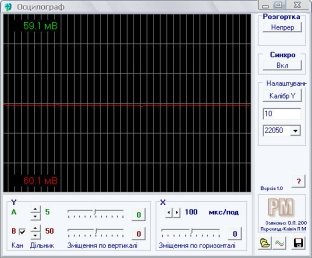Ми бачили, що в коливальному контурі відбуваються ко­ливання напруги, сили струму, заряду на обкладинках кон­денсатора та інших електромагнітних величин 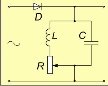(напруже­ності електричного поля, індукції магнітного поля тощо). Тепер потрібно встановити, якими параметрами коливаль­ного контуру визначаються період і частота коливань. Для цього можна поставити експеримент з використанням віртуального елек­тронного осцилографа. Складемо електричне коло за схе­мою, наведеною на малюнку, змінний струм подамо від реального генератора. (Електричне коло до лінійного входу  звукової карти комп’ютера під’єднує вчитель!).  Досліджуване коло містить напівпровідниковий діод, який пропускає до контуру струм промислової частоти (50 Гц - 50 коливань за секунду) лише в один з півперіодів, тобто протягом 0,01 с. У другий півперіод струм через діод не проходить. Однак у перший півперіод конденсатор контуру зарядився, тому в другий півперіод він розряджатиметься через котушку і реостат, і в контурі виникатимуть затухаючі електромагнітні коливання.

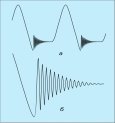На екрані осцилографа можна спос­терігати графік зміни напруги на об­кладинках конденсатора (мал. а) - графік півперіоду змінного струму промислової частоти (половини синусоїди) і графік затухаючих коливань (мал. б), який нас, власне, і цікавить.

Тепер, коли ми знаємо, що затухаючі коливан­ня відбуваються протягом 0,01 с, за допомогою ручок керування роботою осцилографа можемо одержати на екрані лише графік затухаючих коли­вань і визначити їх частоту й період. За 0,01 с відбувалось 20 коливань. Отже, частота коливань - кількість коливань за одну секунду – дорівнює 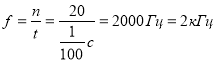(6).

Період коливань дорівнює - 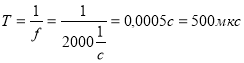(7).

Дослідимо залежність частоти коливань від ємності конденсатора в коливальному контурі. Зафіксуємо три послідовні фази експерименту (мал. 1 а, б, в). На першому з них наведено графік коливань для ємності конденсатора 0,25, на другому - 0,5 і на третьому - 1 ,0 мкФ.

 

 

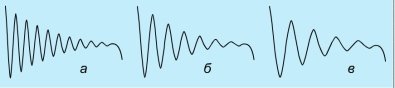
Мал. 1 Дослідження залежності частоти (періоду) електромагнітних коливань від ємності та Індуктивності конденсатора

Індуктивність котушки контуру та його активний опір при цьому залишаються сталими.

Завдання. За даними графіків пропонуємо учням встановити залежність частоти коливань від ємності конденса­тора.

У першому випадку протягом 0,01 с відбулося 10 повних коливань. Отже, частота коливань 1000 Гц. Коли ємність конденсатора збільшили вдвічі, частота коливань виявилася такою, що дорівнює 700 Гц, а коли ємність конденсатора збільшили ще вдвічі (у 4 рази порівняно з початковою), то частота зменшилася до 500 Гц. З цих результатів можна зробити висновок: зі збільшенням ємності конденсатора вдвічі, частота коливань зменшується у - рази.

Отже, ~  (8), T~ (9).

 

 

Далі аналогічно дослідимо залежність частоти коливань від індуктивності котушки. Відомо, що індуктивність котушки L залежить від кількості витків у ній, її конфігурації, а також від наявності в ній феромагнітного осердя. Яким же із зазначених способів зміни індуктивності варто скористатись у досліді? Конфігурацію котушки змінити досить складно. Збільшити кількість витків у котушці вдвічі досить просто, але при цьому зміниться й активний опір котушки і, можливо, саме він впливатиме на значення частоти. Тому збільшуватимемо індуктивність котушки внесенням в неї феромагнітного осердя. В момент внесення осердя індуктивність котушки зростає, а частота коливань зменшується.

 

 

 

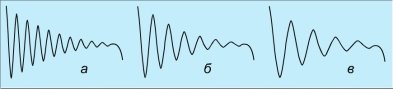
Мал.2. Дослідження залежності частоти (періоду) електромагнітних коливань від ємності та індуктивності конденсатора

На мал.2 б наведено фазу досліду, коли індуктивність котушки більша у 2 рази, ніж для випадку, зображеному на малюнку а, частота коливань тут 700 Гц. У міру подальшого збільшення індуктивності ще вдвічі (мал. в) частота дорівнює 500 Гц. Зрозуміло, що тут маємо таку саму залежність, як і при збільшенні ємності конденсатора. Частота коливань виявляється обернено пропорційною кореню квадратному з індуктивності котушки:

f~ (10),  T~ (11).

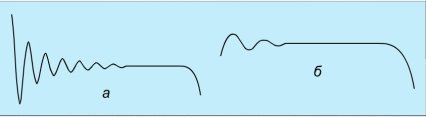
Мал.3. Вплив активного опору контуру на характер вільних електромагнітних коливань

Дослід показує, що зі збільшенням значення активного опору контуру амплітуда коливань швидко зменшується, коливання значно швидше припиняються. Однак активний опір на частоту коливань помітно не впливає (нижче побачимо, що такий вплив все-таки є). На практиці для визначення частоти коливань у коливальному контурі часто користуються формулою Томсона   f=(12),  T=2 (13)   (1853 р.), де f - частота коливань, Гц; Т- період коливань, с; L - індуктивність, Гн; С - ємність, Ф.

Виведення формули Томсона

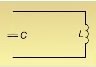Розглянемо коливальний контур з L і С. Повна енергія цього контуру:W= (14),

де q - миттєве значення заряду конденсатора, що дорівнює q = Q_maxsin; / - миттєве значення току в котушці;  Q_max  - максимальний заряд конденсатора.

Домножуємо ліву і праву частину рівняння (14)  на2С:

(15).

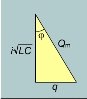Рівняння  являє собою теорему Піфагора (див. мал.) Звідси маємо (16).

Миттєвий заряд на конденсаторі q= (17).

Якщо взяти похідну від миттєвого значення, то (18).  Алe  i= (19).Тоді, врахувавши формули (16), (18) отримаємо: (20). Тоді в врахуванням формули (20) отримаємо вираз   T=2 (21).  Тобто,   T=2(22).

З останнього досліду можна зробити важливий висновок: не завжди в електричному колі, яке складається з котушки і конденсатора, можливі електромагнітні коливання. Якщо опір електричного кола досить значний, то після заряджання конденсатора він розрядиться через котушку зі значним опором. Однак при цьому енергія електричного поля конденсатора перетвориться на теплоту і конденсатор унаслідок явища самоін­дукції не перезарядиться. Матиме місце так зване аперіодичне розряджання конден­сатора.

Встановимо умови, за яких коливання можливі, а за яких - ні. Однак для цього потріб­но докладно проаналізувати явища в коливальному контурі з використанням математич­ного апарату.

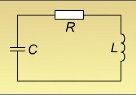Уявімо собі коливальний контур, до складу якого входить конденсатор С, котушка L та активний опір R . Нехай у певний момент часу конденсатор зарядили до напруги U і від'єднали зовнішнє джерело живлення. Якби в електричному колі був лише резистор R, то струм протікав би лише доти, доки потенціали обкладинок конденсатора не зрівнялися. Якщо ж у колі є котушка з індуктивністю L, то в той момент, коли потенціали обкладинок конденсатора зрівняються, електрорушійна сила самоіндукції, що виникає в котушці при зміні сили струму в ній, підтримає струм, який зменшується, і відбудеться перезарядження обкладинок конденсатора. Після цього струм у контурі йтиме у протилежному напрямку, конденсатор знову пере­зарядиться і т. д. Виникають електромагнітні коливання, які ми вже дослідили експери­ментально.

Під час вільних коливань у контурі між напругою і силою струму встановлюється певне співвідношення, яке визначається параметрами контуру. Сила струму в двох контурах за однакової амплітуди напруги може бути різною. Тому контур характеризують так званим хвильовим (або характеристичним) опором.

Якщо знехтувати втратами енергії в контурі, то можна вважати, що максимальне значення енергії магнітного поля котушки дорівнює максимальному значенню енергії електричного поля конденсатора: (23). Звідси можна знайти співвідношення між амплітудою сили струму й амплітудою напруги: 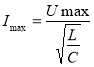(24). Вираз має розмірність опору. Це і є хвильовий або характеристичний опір.

Щоб з'ясувати фізичний зміст характеристичного опору, розглянемо два контури, час­тоти власних коливань яких однакові, а конденсатори різних ємностей, наприклад С₁<С₂. Обидва конденсатори заряджаються до однакової напруги, але в першому контурі запас енергії менший, ніж у другому. Відповідно, й амплітуда сили струму в першому кон­турі буде менша. Тому вважають, що хвильовий опір першого контуру більший, ніж другого.

 

V. Корекція знань учнів.

1. Що можна вважати коливальним контуром?
2. Які фізичні величини є характеристиками (параметрами) коливального конту­ра?
3. Які перетворення складових електромагнітної енергії спостерігаються в коли­вальному контурі?
4. Чому вільні коливання в контурі затухають?
5. Чи завжди в електричних колах, що мають індуктивність і ємність, можуть спостерігатись електромагнітні коливання?
6. Як встановлюються умови існування вільних електромагнітних коливань в електричних колах? Що характеризує хвильовий опір?

 

Інтерактивна вправа «Продовж  думку».

Учитель починає, учень закінчує і продовжує ланцюжок і т.д., помилку виправляє той, хто розпочинав речення.

Наприклад:

• Період коливань в контурі залежить від…
• Якщо опір провідників в контурі буде досить великим, то коливання…
• Якщо ємність конденсатора в контурі збільшити в 4 рази, то період коливань,,,
• Якщо індуктивність котушки  в контурі зменшити  в 4 рази, то період коливань,,,
• Період коливань в контурі становить 0,1 с, тоді частота коливань рівна…

VI. Підсумки уроку

Міні-виступ «Що я сьогодні відкрив для себе?»

Учні говорять про відкриття, яке вони зробили для себе на уроці. Відкриття може бути і емоційним, а не тільки фізичним.

VII. Домашнє завдання

Розташувати в порядку зростання частоти коливань контури з такими параметрами L і  C: а)10мкФ, 1 Гн, б) 1 мкФ, 20 Гн, в) 40 мкФ, 0,5 Гн, г) 10 Гн, 10 мкФ.

 

http://pmklinich.blogspot.com/