Урок з алгебри в 7-му класі

Тема уроку: Рівняння з двома змінними. Лінійні рівняння з двома

                      змінними

Мета уроку: закріпити знання учнів про рівняння з двома змінними;

                      формування вмінь учнів розв’язувати лінійні рівняння з        

                      двома  змінними;

                      розвивати дослідницькі здібності учнів, логічне мислення,

                      виховувати старанність, самостійність;

                      сприяти формуванню особистості

Тип уроку: нестандартний урок застосування умінь та навичок

Обладнання: таблиця «Лінійні рівняння», кросворд, плакат з девізом

                        уроку, мікрофон, аркуші паперу з рівняннями,

                        кольорові картки для проведення гри «Естафета», картки

                        із індивідуальними завданнями

Хід уроку

1.     Вступне слово вчителя

 

Сьогодні у нас незвичайний урок на якому ми з вами повторимо і закріпимо знання про лінійні рівняння з двома змінними. Проведемо декілька ігор математичної вікторини, навчимося розв’язувати лінійні рівняння з двома змінними. Сподіваюсь, що форма проведення сьогоднішнього уроку допоможе вам краще засвоїти вивчений матеріал. Як говорить давня мудрість:

 

    «Скажи мені - і я забуду,

      Покажи мені – і я запам’ятаю,

      Дай мені діяти самому – і я навчуся…»  

2.     Актуалізація опорних знань і вмінь учнів

Спочатку ми перевіримо ваше домашнє завдання. Ви всі вдома готувалися до сьогоднішнього уроку. Тому уявімо собі, що ви дослідники, які довго вивчали рівняння з двома змінними. У ваш інститут приїхала журналістка з журналу «Математичний вісник».Вона готує статтю в журнал про рівняння з двома змінними і хоче взяти від вас інтерв'ю.

Журналістка: «Добрий день. Мене звуть О.В., журнал «Математичний вісник».  Я готую статтю про рівняння з двома змінними. Дізналась про ваші  дослідження і у мене виникли деякі запитання:

1. Поясніть будь – ласка, що називається рівнянням з двома змінними?

Учень 1: Рівність, яка містить дві невідомі x та y, називається рівнянням з двома змінними.

2. Наведіть будь – ласка, приклади рівнянь з двома змінними.

Учень 2: Приклади рівнянь з двома змінними:

                  5х + 3у = 22; ху =8; 2х= 3у; у²+х =6.

3. Що називають розв’язком рівняння з двома змінними?

Учень 3: Розв'язком рівняння з двома змінними, називається пара значень змінних, які перетворюють це рівняння у правильну рівність.

4. Як записують розв’язок рівняння з двома змінними?

Учень 4: Розв’язок рівняння записують в круглих дужках через крапку з комою таким чином: (2;8). У записі розв’язку рівнянь з двома  змінними х і у на першому місці ставлять значення змінної х, а на другому – значення -у.

5. Скажіть будь – ласка, які рівняння називаються рівносильними?

Учень 5: Рівняння з двома змінними які мають одні й ті самі розв’язки,                                                                           називаються рівносильними. Рівняння, які не мають розв’язків, теж називаються рівносильними .

6. Які властивості мають рівняння з двома змінними?

Учень 6: Рівняння з двома змінними мають такі самі властивості, як і рівняння з однією змінною. У рівнянні з двома змінними доданки можна переносити з однієї частини рівняння в іншу, змінивши знаки цих доданків; обидві частини рівняння можна перемножити або поділити на одне й те саме, відмінне від нуля, число. При цьому дістанемо рівняння рівносильне даному.

7. Яким чином розв’язують рівняння з двома змінними?

Учень 7: Щоб знайти розв’язок рівняння з двома змінними можна підставити в нього замість х довільне число, або виразити одну змінну через іншу. Наприклад:

  5х +3у = 22                            5х + 3у = 22

   х = 2                                       5х = 22 – 3у/ 5

   5·2 + 3у = 22                           х = 4,4 – 0,6у

   у = 4

8. Що називають лінійним рівнянням з двома змінними?

Учень 8: Рівняння виду ах + by = c, де a, b, c – деякі числа, називається лінійним рівнянням з двома змінними.

9. Що називається лінійним рівнянням першого степеня з двома змінними?

Учень 9: Рівняння виду ах + bx =c, де a# 0, b# 0, називаються рівнянням першого степеня з двома змінними.

Тепер надаємо слово голові дослідницької групи.

       Історична довідка

  Лінійні рівняння з одним невідомим вміли розв’язувати ще в давньому Вавилоні та Єгипті більш ніж 4 тис. р. тому. Єгипетські жерці шукане невідоме число називали 2хау2 (у перекладі «куча») і позначали спеціальним знаком. У папірусі, що дійшов до нас є така задача:

      «Куча та її сьома частина складають 19. Знайти кучу.»

Задача зводиться до розв’язання рівняння: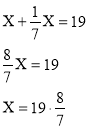                   

Подібні задачі вміли розв’язувати вчені Стародавньої Греції, Індії, Китаю.

3. Формування вмінь і навичок учнів

Дякуємо за інтерв'ю, а тепер коли ми повторили відомості про рівняння з двома змінними, пропоную вам математичну вікторину. В кінці уроку за активність і правильні відповіді ви отримаєте оцінки. Отже розпочинаємо:

 

1.               Які з пар (-1;6), (6;-1), (1;1), (0;0), (1;-5) є

розв’язками рівняння ху + у = 0.

2.  Розв’язком якого з наведених рівнянь є пара (1;1)

А) х +у =1;

Б) ху = 1;

В) х²+ у² = 1;

Г) ху = -1.

3. Підберіть декілька розв’язків рівняння:

            А) х – у = 10;

            Б) ху = 10;

            В) х/ц = 10.

4. Знайдіть розв’язок рівняння  5х + 3у = 22.

                        Проведення гри «Хто швидше?»

Складіть рівняння із змінними х і у, розв’язком якого є пара: (2;1), (2;3).

     Розв’язування кросворду «Що вивчає алгебра?»

Р

І

В

Н

Я

Н

Н

Я

                                                                                    

                               2               

                                 

                               3   

                               5  

 

                              4

                              1                              

                              5  

                           

 

1. Що вивчає алгебра?
2. Рівняння, що мають спільні розв’язки або взагалі не мають розв’язків, називають…
3. Це означає знайти всі розв’язки рівняння або показати, що їх не має.
4. Невідомі числа в рівнянні називають…
5. Рівність, яка містить невідомі числа.

 

                      Проведення гри «Естафета»

             Клас розбивається на сектори за кольором:

             

 Червоний – високий рівень знань;

                Зелений – достатній рівень знань;

                Синій – низький рівень знань;

 

 Учні кожного ряду одержують картку свого кольору, на якій записані рівняння. Потім по черзі розв’язують по одному рівнянню з карти і записують результати в графу «розв’язок» і передають картку іншому учневі свого ряду. Виграє той ряд, учні якого першими розв’яжуть правильно всі рівняння.

                           

Виразіть змінну х через у

Червона
3х + 4у = 12
4х – 2у = 20
5х – 3у = 5
6х + 5у = 11
15х – 10у = 40

 

 

 

Зелена 1
ху = 24
х – у = 5
ху = 49
х – у = 8
х + у =15

 

 

Зелена 2
х + у = 6
ху = 12
х – 4у = 16
ху = 25
ху = 36

 

 

Синя
х– у = 12
у – х = 10
х + у = 35
у +х = 24
у – х = 7

    

  4.Розв’язування задач

Декілька учнів отримують картки з індивідуальними завданнями.

    Один учень розв’язує задачу з поясненням.

Задача: Є труби завдовжки 7м і 8м. Скільки треба взяти тих і тих, щоб прокласти  трубопровід завдовжки 67м?          

                                            

    Розв’язання

Нехай треба взяти х труб завдовжки 7м, і у труб завдовжки 8м, тоді за умовою задачі маємо рівняння: 7х + 8у = 67. Знайдемо натуральні розв’язки цього рівняння. Значення змінної у не може бути більшим за 8. бо значення виразу

7х + 8у при натуральному значенні х і у = 8, більше ніж 7·1 + 8·8 = 7 + 64 = 71. Знайдемо значення змінної х:

 

Якщо у = 1, то 7·х + 8 = 67

                           7х = 59

                            х = 8    , (8;1)

Якщо у = 2, то  7х + 16 = 67

                            7х = 51

                              Х = 7    , (7;2) 

Якщо у = 3 , то 7х +24 = 67

                            7х = 43

                             х = 6       , (6;3)

Якщо у = 4 , то (5;4)

Якщо у =5 , то (3;5)

Якщо у = 6, то

Якщо у = 7, то             

                               

Серед даних розв’язків умову задачі задовольняє пара (5;4). Отже, щоб прокласти трубопровід завдовжки 67 м, слід взяти 5 труб завдовжки 7м

і 4 труби довжиною 8м.

 

 

5.  Підведення підсумків уроку

Запитання до класу

1)Скільки розв’язків має рівняння?

   0·x=0

   0·x=5

   8х + 6у = 10

   4х + 3у = 7

2)Доповідь на тему «Математика».

         (підготували декілька учнів самостійно)

3)Вислови про математику

«У математиці слід пам’ятати не формули, а процес мислення»

         (В. Єрмаков)

 

«Природа формує свої закони мовою математики»

         (Г. Галілей)

 

«Ми ніколи не станемо математиками, навіть знаючи напам’ять усі чужі доведення, якщо наш розум не здатний самостійно розв’язувати які б то не було проблеми»                                                                                           

            (Р. Декарт)

 

«Математика – це мова плюс міркування, це наче мова і логіка разом. Математика – це знаряддя для міркування. У ній сконцентровано результати точного мислення багатьох людей»                                             

            (Р. Фейман)

 

4.               Оголошення оцінок; відповісти на запитання учнів.

6.                 Домашнє завдання: вивчити § 21, вправи №391, 393.