Урок з алгебри "Застосування формул скороченог множення". 7 клас
Стандарти нового покоління базуються на переведенні навчального процесу з пояснювального на діяльнісний метод навчання, в основі якого лежить «рефлексія самоорганізації» - виникло утруднення, значить треба припинити діяти і почати думати. Представлений урок побудовано відповідно до технології діяльнісного методу, урок за типом - ТР (тренувально-рефлексивний ). На кожному етапі уроку вказано види універсальних навчальних дій, які необхідно сформувати в учнів. Використання технології забезпечує досягнення високих результатів як в освоєнні знань і навичок, так і в загальному розвитку учнів. На уроках з використанням даної технології учні вчаться краще міркувати, думати, аналізувати, не боятися труднощів, самостійно вирішувати проблеми, які поставлені перед ними, ставити цілі і їх досягати, бути творчими особистостями. Вони вчаться спілкуватися, поважати думку кожного і рахуватися один з одним.
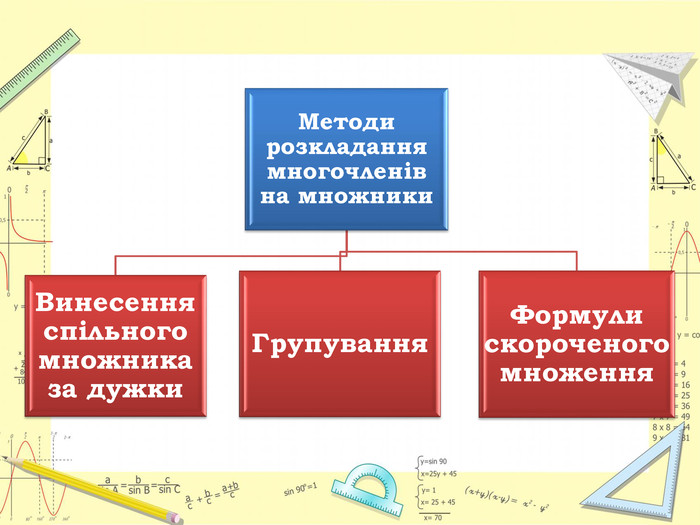
Робота містить презентацію, яка може бути використана при вивченні теми «Застосування формул скороченого множення при розкладанні многочленів на множники». Використані основні поняття теми «Розкладання на множники»: формули, методи та прийоми, алгоритми при застосуванні формул до розв'язування задач та рівнянь.
- ÅÉêÉÄäìêùÄ 2015.docx docx
- éêæÆÇéèÇ.doc doc
- 2 ßΓ«α_¡¬á.docx docx
- 3 ßΓ«α_¡¬á. Ç¡«Γáµ_∩.docx docx
- Показати всі файли


ПРИРОДНИЧО-МАТЕМАТИЧНА
ОСВІТА
Л.М. Вовк
РОЗКЛАДАННЯ МНОГОЧЛЕНІВ НА МНОЖНИКИ


|
|
||
|
|
Л.М. Вовк
РОЗКЛАДАННЯ МНОГОЧЛЕНІВ НА МНОЖНИКИ
|
|
|
|
|
|
ДЕПАРТАМЕНТ ОСВІТИ І НАУКИ
ДНІПРОПЕТРОВСЬКОЇ ОБЛАСНОЇ ДЕРЖАВНОЇ АДМІНІСТРАЦІЇ
ДНІПРОПЕТРОВСЬКИЙ ОБЛАСНИЙ ІНСТИТУТ ПІСЛЯДИПЛОМНОЇ ПЕДАГОГІЧНОЇ ОСВІТИ
МІСЬКИЙ ВІДДІЛ ОСВІТИ ВИКОНКОМУ ПЕРШОТРАВЕНСЬКОЇ МІСЬКОЇ РАДИ
ПЕРШОТРАВЕНСЬКА ЗАГАЛЬНООСВІТНЯ ШКОЛА І-ІІІ СТУПЕНІВ № 3
Розкладання многочленів на множники
Дніпропетровськ
2015
Автор: Вовк Лариса Миколаївна, вчитель математики Першотравенської загальноосвітньої школи І-ІІІ ступенів № 3
Стандарти нового покоління базуються на переведенні навчального процесу з пояснювального на діяльнісний метод навчання, в основі якого лежить «рефлексія самоорганізації» - виникло утруднення, значить треба припинити діяти і почати думати. Представлений урок побудовано відповідно до технології діяльнісного методу, урок за типом - ТР (тренувально-рефлексивний ). На кожному етапі уроку вказано види універсальних навчальних дій, які необхідно сформувати в учнів. Використання технології забезпечує досягнення високих результатів як в освоєнні знань і навичок, так і в загальному розвитку учнів. На уроках з використанням даної технології учні вчаться краще міркувати, думати, аналізувати, не боятися труднощів, самостійно вирішувати проблеми, які поставлені перед ними, ставити цілі і їх досягати, бути творчими особистостями. Вони вчаться спілкуватися, поважати думку кожного і рахуватися один з одним.
Робота містить презентацію, яка може бути використана при вивченні теми «Застосування формул скороченого множення при розкладанні многочленів на множники». Використані основні поняття теми «Розкладання на множники»: формули, методи та прийоми, алгоритми при застосуванні формул до розв’язування задач та рівнянь.
Алгебра, 7 клас
Тема уроку: Розв’язування задач та рівнянь за допомогою розкладання многочленів на множники.
Основні цілі:
1) тренувати вміння розкладати многочлени на множники і застосовувати це вміння при розв’язуванні задач і рівнянь;
2) тренувати вміння знаходити значення виразів;
3) формувати різні групи компетенцій:
- соціальні – готовність до самостійного пошуку розв’язання проблеми, вміння спілкуватись;
- полікультурні – вміння застосовувати здобуті знання на практиці опановувати засади культурного спілкування в ході обговорення питань заняття; розвивати вміння робити висновки;
- інформаційні – вміння знаходити додаткову інформацію з історії розвитку математики та використовувати її для розширення кругозору;
- самоосвітні – вміння працювати з книгою, мати бажання до навчання; розвивати пам’ять, увагу, творчий підхід до розв’язання проблем;
4) виховувати культуру математичного мовлення, упевненість у своїх силах, бажання здобувати знання.
Тип уроку: тренувально-рефлексивний
Демонстраційний матеріал:
1) формула квадрата суми і різниці виразів;
2) формула добутку різниці і суми;
3) формула різниці квадратів;
4) формула куба суми;
5) формула куба різниці;
6) формула різниці кубів;
7) формула суми кубів;
8) правило винесення спільного множника за дужки;
9) алгоритм розкладання многочлена на множники;
10) спосіб групування;
11) способи перетворення многочленів, які можна використовувати при групуванні;
12) алгоритм розкладання многочлена на множники методом групування;
13) способи перетворення многочленів, які можна використовувати використовувані при групуванні;
14) поради;
15) алгоритм розв’язування задач за допомогою розкладання многочлена на множники:
|
1. Скласти рівняння за текстом задачі. 2. Представити рівняння так, щоб праворуч стояв 0. 3. Розкласти многочлен, що стоїть в лівій частині на множники. 4. Розв’язати рівняння. 5. Вибрати розв’язки, що задовольняють умові задачі. 6. Відповісти на запитання задачі. |
16) картка з питаннями для етапу рефлексії;
Роздатковий матеріал:
1) детальний зразок виконання завдань домашньої роботи:
|
1. Розв’язати рівняння: |
|
|
а) a2 + 2a – 15 = 0; (a2 + 2a + 1) − 1– 15 = 0; (а + 1)2 – 16 = 0; (а + 1 – 4)(а + 1 + 4) = 0; (а – 3)(а + 5) = 0; а – 3 = 0 або а + 5 = 0 а = 3; а = − 5. Відповідь: {− 5; 3} |
б) 2b2 + 2b – 12 = 0; 2(b2 + b – 6) = 0;
2((b2 + 2 ∙ b ∙
2((b +
2(b + 2(b – 2)(b + 3) = 0; b – 2 = 0 або b + 3 = 0; b = 2; b = − 3. Відповідь: {− 3; 2} |
|
2. Розкладіть на множники: а) x3 + 27 + 7x2 + 21x = (x3 + 27) + (7x2 + 21x) = (х + 3)(х2 – 3х + 9) + 7х(х + 3) = = (х + 3)(х2 – 3х + 9 + 7х) = (х + 3)(х2 + 4х + 9); б) y4 – y3 – y + 1 = (y4 – y3) – (y – 1) = у3(у – 1) – (у – 1) = (у – 1)(у3 – 1) = = (у – 1)(у – 1)(у2 + у = 1) |
|
|
3. Знайдіть значення виразу: а) xy2 + x2y = ху(у + х) Якщо xy = 5, x + y = 8, то 5 ∙ 8 = 40; б) 9z2 – 12zt + 4t2 = (3z – 2t)2 = (2t – 3z)2 Якщо 2t – 3z = 9, то 92 = 81 |
|
|
4. Скоротити дроби при допустимих значеннях змінних:
а)
=
б)
= |
|
2) детальний зразок виконання завдання в групах:
|
1) 4z(z + 2) = 32z + 13; 4z(z + 2) − 32z – 13 = 0; 4z2 + 8z − 32z – 13 = 0; 4z2 − 24z – 13 = 0; ((2z)2 – 2 ∙ 2z ∙ 6 + 62) − 36 – 13 = 0; (2z – 6)2 – 49 = 0; (2z – 6 – 7)(2z – 6 + 7) = 0; (2z – 13)(2z + 1) = 0; 2z – 13 = 0 або 2z + 1 = 0 2z = 13 2z = − 1 z = 6,5 z = − 0,5 Відповідь: {− 0,5; 6,5} Широта ( z1 + z2) : 6 – 1 |
2) t2(14 – t) = 6t(2t – 4); 14t2 – t3 = 12t2 – 24t; 14t2 – t3 − 12t2 + 24t = 0; – t3 + 2t2 + 24t = 0; − t(t2 – 2t – 24) = 0; − t((t2 – 2t + 1) − 1– 24) = 0; − t((t – 1)2 − 25) = 0; − t(t – 1 − 5)(t – 1 + 5) = 0; − t(t − 6)(t + 4) = 0; t = 0 або t = 6 або t = − 4 Відповідь: {− 4; 0; 6}
Східна довгота t1t3 +124 |
|
Розв’язати задачу: «Велосипедисти на першому етапі змагань протягом 9 годин рухались з середньою швидкістю х км/год., а на другому етапі вони рухались на х годин більше з середньою швидкістю на 9 км/год. більшою. З якою середньою швидкістю їхали велосипедисти на першому етапі, якщо другий етап становив 900 км? а) На другому етапі час руху (9 + х) год., а швидкість руху (х + 9) км/год., де 9 + х > 0, х + 9 > 0. Відомо, що друга частина шляху дорівнює 900 км.
(9 + х)(х + 9) = 900; 9 + х > 0, х + 9 > 0; (9 + х)(х + 9) = 900; (9 + х)2 – 302 = 0; (9 + х – 30)(9 + х + 30) = 0; (х – 21)(х + 39) = 0; х – 21 = 0 або х + 39 = 0 х = 21 х = − 39 Корінь х = 21 задовольняє всі умови, а корінь х = – 39 не задовольняє умову 9 + х > 0. Відповідь: на першому етапі середня швидкість дорівнює 21 км/год. |
3) карточка фіксації результатів роботи в групах:
|
Прізвище, ім’я |
Завдання, які виконані вірно |
Завдання, при виконанні яких виникли труднощі |
Виникли труднощі |
|||||
|
ДЗ |
ТЗ |
ДЗ |
ТЗ |
Місця труднощів |
Причини труднощів |
|||
|
ДЗ |
ТЗ |
ДЗ |
ТЗ |
|||||
|
|
|
|
|
|
|
|
|
|
4) еталон для самоперевірки самостійної роботи:
|
1) 7x(х + 1) = 21 – 7х; 7х2 + 7х = 21 – 7х; 7х2 + 7х − 21 + 7х = 0; 7х2 + 14х – 21 = 0; 7(х2 + 2х – 3) = 0; 7((х2 + 2х + 1) – 1 – 3) = 0; 7((х + 1)2 – 4) = 0;
7(х + 1 – 2)(х + 1 + 2) = 0;
7(х – 1)(х + 3) = 0; х – 1 = 0 або х + 3 = 0 х = 1; х = − 3.
Відповідь: {− 3; 1} |
1) Перетворити рівняння, так, щоб праворуч стояв 0 .
2) Звести подібні доданки. 3) Винести спільний множник 7 за дужку. 4) Додати і відняти 1. 5) Записати тричлен, як квадрат суми а2 + 2аb + b2 = (а + b)2
6) Застосувати формулу різниці квадратів (а2 – b2 = (a – b)(a + b)).
7) Добуток дорівнює 0 тоді, коли хоча б один з множників дорівнює 0. 8) Знайти корені. 9) Записати відповідь. |
|
2) у(у – 1) = у + 15; у2 – у = у + 15; у2 – у − у – 15 = 0; у2 – 2у – 15 = 0; (у2 – 2у + 1) – 1 – 15 = 0; (у – 1)2 – 16 = 0;
(у – 1 – 4)(у – 1 + 4) = 0; (у – 5)(у + 3) = 0; у – 5 = 0 або у + 3 = 0 у = 5 у = − 3
Відповідь: {− 3; 5} |
1) Перетворити рівняння, так, щоб праворуч стояв 0 . 2) Звести подібні доданки. 3) Додати і відняти 1. 4) Записати тричлен, як квадрат суми а2 + 2аb + b2 = (а + b)2 5) Застосувати формулу різниці квадратів а2 – b2 = (a – b)(a + b)). 6) Добуток дорівнює 0 тоді, коли хоча б один з множників дорівнює 0. 7) Знайти корені. 8) Записати відповідь. |
5) карточка для рефлексії:
|
|
Домашня работа (вказати номери завдань) |
Тренувальні вправи (вказати номери завдань) |
Самостійна робота (вказати номери завдань) |
|
Виконано без помилок |
|
|
|
|
Виникли труднощі |
|
|
|
|
Теми, над якими необхідно працювати |
|
||
Хід уроку
1. Мотивація до навчальної діяльності
мета:
1) включення учнів у навчальну діяльність;
2) організувати діяльність учнів з установки тематичних рамок: розкладання многочленів на множники;
3) створити умови для виникнення в учня внутрішньої потреби включення в навчальну діяльність.
Організація навчального процесу на етапі 1:
- Які способи розкладання на множники многочленів ви знаєте?
- З якою метою треба вміти розкладати многочлени на множники?
Я хочу розпочати наш урок із казки “Пряник і колосок”, яку написав своєму сину відомий педагог В.О. Сухомлинський.
Вранці, до сходу сонця, Людина взяла білий пряник і пішла в поле. Зірвала колосок у полі, вийняла з нього зернята, і спробувала на зуб, посміхнулася і заховала колосок у кишеню. Ось там і зустрілися Пряник і Колосок.
- Хто ти такий? - запитав Пряник.
- Я колосок.
- Ой, який ти колючий! Яка з тебе користь?
Посміхнувся Колосок, поворухнув своїми вусиками і відповів:
— Без мене не було б ні хліба, ні сухаря, ні тебе, Прянику.
- Отже, - каже Пряник, - все від тебе. Але хто ж над тобою старший?
- Праця, - відповідає Колосок, - вона все дає. Але праця в руках Людини. Праця і Людина – найголовніше.
Отже, я вас закликаю до наполегливої праці, щоб пізнати істину міркувань. Сьогоднішня наполеглива праця дасть нам можливість удосконалити свої навички в розв’язуванні вправ і задач з використанням формул скороченого множення. Дані знання, вміння і навички вам знадобляться не лише на уроках математики, а й на фізиці та хімії.
2. Самостійна діяльність за відомою нормою
мета:
1) організувати самостійне відтворення відомих способів дій, достатніх для виконання тренувальних завдань;
2) організувати наведення прикладів на відтворені способи дій;
3) зафіксувати відтворені способи дій в мові;
4) зафіксувати відтворені способи дій в знаках ( еталони);
5) організувати актуалізацію розумових операцій, достатніх для виконання тренувальних завдань: аналіз, порівняння, узагальнення;
6) організувати узагальнення актуалізованих способів дій;
7) організувати подання спектра завдань, що вимагають тренування розглянутих способів дій.
Організація навчального процесу на етапі 2:
- Як завжди почнемо роботу з повторення. Якщо ви сьогодні будете вчитися застосовувати вміння розкладати многочлени на множники, що вам необхідно повторити?
На дошці представлені пронумеровані еталони Д−1, Д−14, у кожного організатора карточка результатів роботи групи (Р−3).
У кожного учня карточка рефлексії (Р−5).
Кожній групі надано детальний зразок виконання завдань домашньої роботи. На роботу відводиться 3 хвилини.
Кожна група (організатор або член групи) озвучує результат виконання завдання. Кожна група називає правила, поняття, які були використані при виконанні одного із завдань домашньої роботи.
- А зараз вам пропонується ще раз переглянути виконання домашніх задач та скласти алгоритм ( перерахувати кроки ) для розв’язування задач за допомогою розкладання многочленів на множники.
Учні виконують завдання, по закінченні роботи кожна група пропонує варіант алгоритму, після узгодження алгоритм (Д−15) вивішується на дошку.
Конкурс-розминка «Мозковий штурм»
1. Укажіть за допомогою сигнальних карток номер правильної відповіді. Якщо правильної відповіді немає, то укажіть її.
|
А) (a+b)2
Б) (a
В) a2 Г) (a+b)3
Д) (a
Ж) a3
|
1) ( 2) a3+3a2b+3ab2+b3
3) a3
4) (a+b)·(a2
5) (a
6) a2
7) (b
8) (a
9) ( 10) a2+2ab+b2 11) (b+a)2
12) ( |
3. Побудова плану роботи
мета:
1) організувати постановку учнями мети діяльності;
2) організувати визначення учнями засобів (алгоритми, моделі, довідники тощо) для виконання тренувальних завдань;
3) учні будують план роботи з тренувальними завданнями.
Організація навчального процесу на етапі 3:
- Сформулюйте мету вашої подальшої діяльності.
- Що ви будете використовувати при роботі з тренувальними завданнями?
- Як ви будете працювати? ( Будемо виконувати запропоновані завдання, коментуючи виконання кожного завдання, після виконання всіх завдань зіставимо свої роботи з детальним зразком, зафіксуємо правильність виконання завдань, якщо виникнуть труднощі, зафіксуємо місце і причину труднощів, на основі детального зразка виправимо помилки. )
4. Реалізація плану роботи
мета:
1) організувати реалізацію побудованого плану;
2) організувати аналіз отриманих результатів у формі комунікативної взаємодії;
3) організувати фіксацію отриманих результатів;
Організація навчального процесу на етапі 4:
- Учням пропонується серія невірних тотожностей. Завдання групи – знайти помилки, довести їх неправильність і замінити.
|
|
Знайди помилку |
Помилка |
Правильна відповідь |
|
1 |
(4у |
|
|
|
2 |
100m4 |
|
|
|
3 |
(3x+a)2 = 9x2 |
|
|
|
4 |
(6a2 |
|
|
|
5 |
х³+8 = (х+2)(х² |
|
|
|
6 |
(3х+1)³ = 27х³+9х+9х+1 |
|
|
- Розв’язати рівняння та виконати умову. Завдання записуються на дошці:
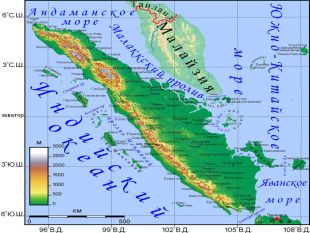
Завдання 1: 4z(z + 2) = 32z + 13; знайти значення ( z1 + z2) : 6 – 1, яке позначає широту географічного об’єкту.
Завдання 2: t2(14 – t) = 6t(2t – 4); знайти значення t1t3 +124, яке позначає східну довготу географічного об’єкту.
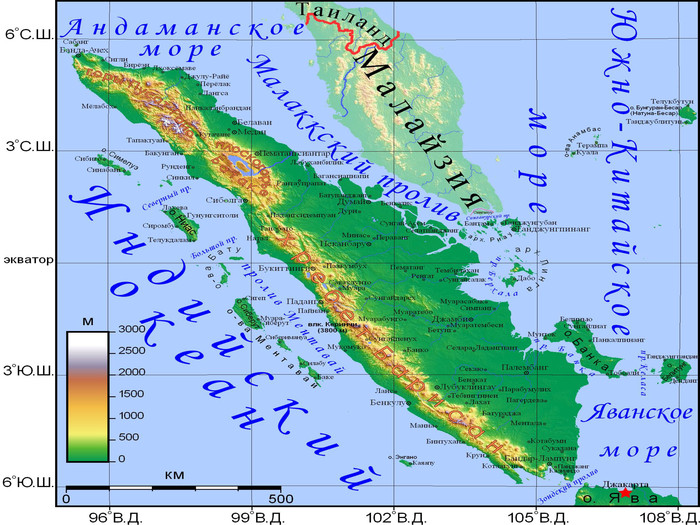
На роботу з вправами відводиться ~10 хвилин. Потім організатори груп узагальнюють результати і заносять в свої таблиці. Один з учнів за допомогою електронної географічної карти знаходить шуканий географічний об’єкт: острів Суматра.
Кожний організатор озвучує результати роботи групи.
5. Узагальнення виниклих утруднень у зовнішній мові.
мета:
організувати обговорювання формулювань способів дій, які викликали утруднення.
Організація навчального процесу на етапі 5:
- Які труднощі у вас виникли при виконанні завдань?
- Чи всі труднощі в групах зняті?
Еталони, при використанні яких були допущені помилки, озвучуються.
Якщо в групах залишилися труднощі при виконанні якихось завдання, то рекомендується розібрати ці завдання на дошці.
6. Самостійна робота з самоперевіркою за зразком
мета:
1) організувати самостійне виконання учнями типових завдань на ті способи дії, які необхідно тренувати;
2) організувати самостійне співвіднесення роботи з еталоном для самоперевірки;
3) за результатами виконання самостійної роботи організувати складання тексту рефлексії діяльності щодо застосування нового способу дії.
Організація навчального процесу на етапі 6:
1)
- Ви працювали всі разом, що далі необхідно зробити?
Для самостійної роботи учням пропонується виконати:
1) 7x(х + 1) = 21 – 7х;
2) у(у – 1) = у + 15.
Учні виконують самостійну роботу, вказуючи еталони, якими користуються при виконанні завдань і проводять самоперевірку за зразком для самоперевірки.
- Проаналізуйте у групах результати виконання самостійної роботи:
- назвіть, які формули, алгоритми ви використовували при виконанні завдань;
- назвіть, в яких місцях і чому виникли труднощі.
2)
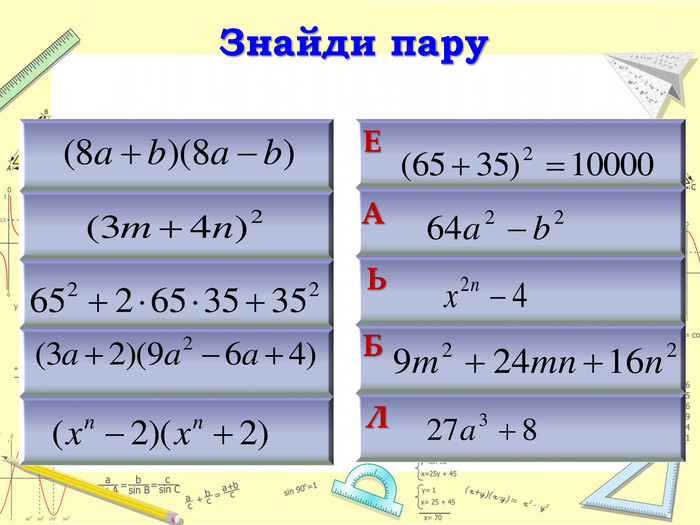
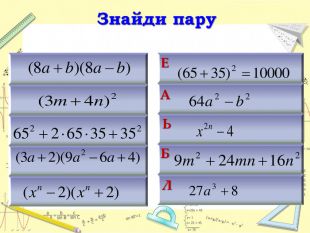
Естафета «Знайди пару». Робота в групах. Ключове слово «Абель». Короткі історичні відомості про Нільса Генріка Абеля.
|
|
|
Е |
|
|
|
А |
|
|
|
Ь |
|
|
|
Б |
|
|
|
Л |
7. Повторення.
мета:
тренувати вміння знаходити значення виразів.
Організація навчального процесу на етапі 7:
Завдання виконуються біля дошки з коментуванням.
- Знайти значення виразу 4p2 + 2pq + 7 – q2 – (–p2 – pq +q2) – 3p2 – (3pq + 2p2) + q2 ,
якщо q = 2:
4p2 + 2pq + 7 – q2 – (–p2 – pq +q2) – 3p2 – (3pq + 2p2) + q2 =
= 4p2 + 2pq + 7 – q2 + p2 + pq − q2 – 3p2 – 3pq − 2p2 + q2 = − q2 + 7
Якщо q = 2, то – 22 + 7 = − 4 + 7 = 3.
8. Рефлексія діяльності на уроці
мета:
1) організувати фіксацію матеріалу, який застосовували на уроці ;
2) організувати оцінювання учнями власної діяльності на уроці;
3) організувати фіксацію недозволених утруднень на уроці як напрямків майбутньої навчальної діяльності;
4) організувати обговорення і запис домашнього завдання;
5) організувати складання тексту по рефлексії діяльності на уроці.
|
|
Домашня робота (вказати задачу) |
Тренувальні вправи (вказати вправи) |
Самостійна робота (вказати вправи) |
|
Виконано без помилок |
|
|
|
|
Виникли труднощі |
|
|
|
|
Теми, над якими необхідно працювати |
|
||
Організація навчального процесу на етапі 9:
- Аналізуючи роботу кожного учасника групи, проаналізуйте роботу всієї групи і дайте відповідь на запитання?
- Які уміння ви сьогодні тренували?
- Яку мету ви ставили перед собою?
- Ви досягли поставленої мети?
- Які знання ви використовували при виконанні завдань?
- Які труднощі виникали в процесі роботи над завданнями?
- Які труднощі виникали ( якщо виникали ) при роботі в групах?
- Які досягнення ви можете відзначити
Проводиться індивідуальна рефлексія .
Домашнє завдання:
п. 4.4.5 . № № 900 (а), 901 (а), 904.
16x2– (4x–5)2 = 15 розв’язати рівняння двома способами.
1
Стандарти нового покоління базуються на переведення навчального процесу з пояснювального на діяльнісний метод навчання, в основі якого лежить «рефлексія самоорганізації» - виникло утруднення, значить треба припинити діяти і почати думати. Представлений урок побудовано відповідно до технології діяльнісного методу, урок за типом - ТР (тренувально-рефлексивний ). На кожному етапі уроку вказано види універсальних навчальних дій, які необхідно сформувати в учнів. Використання технології забезпечує досягнення високих результатів як в освоєнні знань і навичок, так і в загальному розвитку учнів. На уроках з використанням даної технології учні вчаться краще міркувати, думати, аналізувати, не боятися труднощів, самостійно вирішувати проблеми, які поставлені перед ними, ставити цілі і їх досягати, бути творчими особистостями. Вони вчаться спілкуватися, поважати думку кожного і рахуватися один з одним.
Робота містить презентацію, яка може бути використана при вивченні теми «Застосування формул скороченого множення при розкладанні многочленів на множники». Використані основні поняття теми «Розкладання на множники»: формули, методи та прийоми, алгоритми при застосуванні формул до розв’язування задач та рівнянь.

Крок до успіху
Застосування формул
скороченого множення
Бачити і робити нове - дуже велике задоволення.
Вольтер (1694-1778),
французький філософ
«Як показує досвід, ніщо з такою силою, не спонукає високі уми до роботи над збагаченням знань, як постановка важкої і водночас корисної задачі».
Йоганн Бернуллі (1667-1748),
швейцарський математик.
«Істинна і законна мета всіх наук полягає в тому, щоб наділяти життя людське новими винаходами і багатствами».
Френсіс Бекон (1561 – 1626),
англійський філософ і політичний діяч.
«Щоб домогтися якого-небудь прогресу в науках безумовно необхідно займатися окремими проблемами».
Карл Вейєрштрас (1815 – 1897 ),
німецький математик.
Вікно довідок розділу «Формули скороченого множення»
|
Формула |
|
|
|
Добуток різниці двох виразів на їх суму |
|
|
Квадрат суми двочлена |
|
|
Квадрат різниці двочлена |
|
|
Куб суми двочлена |
|
|
Куб різниці двочлена |
|
|
Різниця кубів |
|
|
Сума кубів |
Формула квадрата суми двочлена
Квадрат суми двох виразів дорівнює квадрату першого виразу плюс подвоєний добуток першого виразу і другого виразу плюс квадрат другого виразу.
(а + b)2 = а2 + 2ab + b2
Формула квадрата різниці двочлена
Квадрат різниці двох виразів дорівнює квадрату першого виразу мінус подвоєний добуток першого виразу і другого виразу плюс квадрат другого виразу.
(а − b)2 = а2 − 2ab + b2
Формули скороченого множення
на службі у арифметики
Правило піднесення до квадрату натурального числа, що закінчується на 5 *
Для того щоб піднести до квадрату будь-яке натуральне число, яке закінчується цифрою 5, можна помножити число, отримане після відкидання одиниць, на наступне за ним натуральне число, і до отриманого результату приписати праворуч 25.
Формула квадрата тричлена
Квадрат тричлена дорівнює сумі квадратів всіх його членів, плюс всі попарні подвоєні добутки його членів.
(а + b + с)2 = а2 + b2 + с2 + 2ab + 2bс + 2aс
Формула добутку суми двох виразів і їх різниці
Добуток різниці двох виразів і їх суми дорівнює різниці квадратів цих виразів.
(a – b)(a + b) = a2 – b2
Формула різниці квадратів
Різниця квадратів двох виразів дорівнює добутку їх різниці і їх суми.
а2 − b2 = (a – b)(a + b)
Формула куба різниці двочлена
Куб суми двох виразів дорівнює кубу першого виразу, плюс потроєний добуток квадрату першого виразу на другий, плюс потроєний добуток першого виразу на квадрат другого, плюс куб другого виразу.
(a + b)3 = a3 + 3a2b + 3ab2 + b3
Алгоритм піднесення двочлена до степеня n, n N0*
1. Записати в установленому порядку всі одночлени, яким подібні члени підсумкового многочлена.
2. Записати трикутник Паскаля до (n + 1)-го рядка.
3. Записати послідовно в якості коефіцієнтів виписаних одночленів числа з ( n + 1)-го рядка трикутника Паскаля.
4. При піднесенні до степеня суми (а + b)n поставити перед усіма одночленами знак «плюс».
5. При піднесенні до степеня різниці (а – b)n поставити перед першим одночленом знак «плюс», перед другим - знак «мінус» і далі чергувати знаки «мінус», «плюс» до останнього одночлена.
Формула суми кубів
Сума кубів двох виразів дорівнює добутку суми цих виразів на неповний квадрат їх різниці.
а3 + b3 = (a + b)(a2 − ab + b2)
Формула різниці кубів
Різниця кубів двох виразів дорівнює добутку різниці цих виразів на неповний квадрат їх суми.
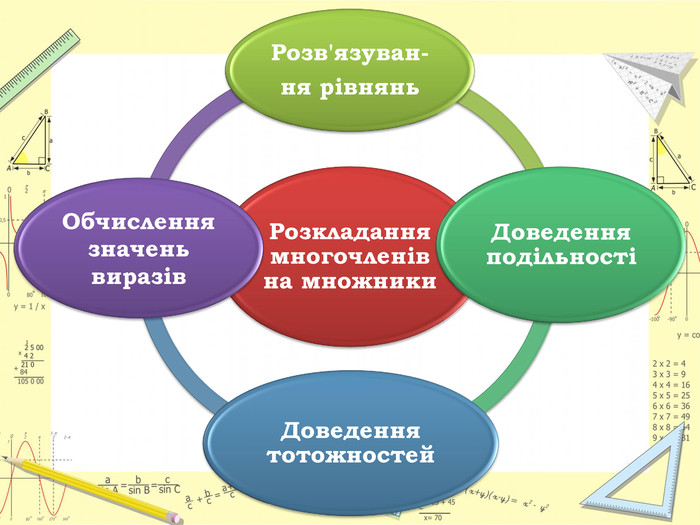
Розкладання многочленів на множники
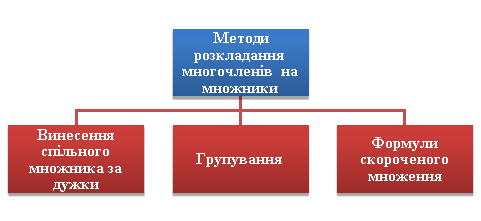
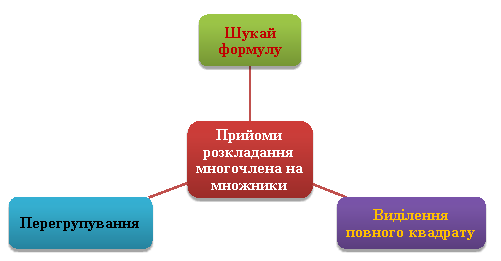
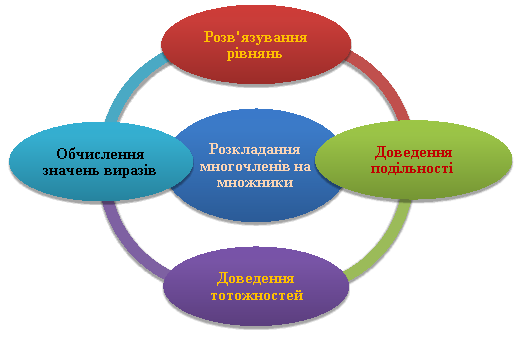

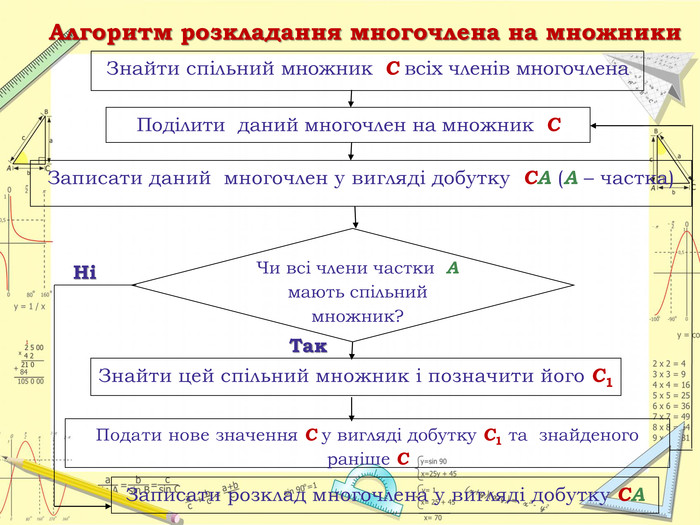
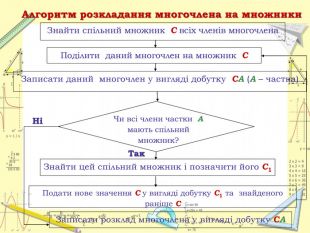
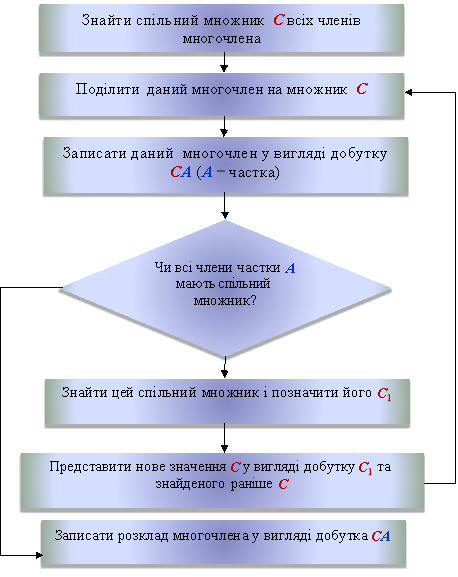 Алгоритм розкладання многочлена на множники
Алгоритм розкладання многочлена на множники
![]()
![]()
 Правило винесения спільного множника за дужки
Правило винесения спільного множника за дужки
 Спосіб групування
Спосіб групування







Сприятлива можливість ховається серед труднощів і проблем
Альберт Ейнштейн (1879-1955),
один із засновників сучасної
теоретичної фізики,
творець теорії відносності.
Математик - це той, хто вміє знаходити аналогії між твердженнями
Стефан Банах ( 1892 – 1945 рр.),
польський математик.
Бачити і робити нове - дуже велике задоволення
Вольтер (1694-1778),
французький філософ.
Все цінне дістається дорогою ціною - найцінніший з металів найтугоплавкіший і найважчий
Грасіан-і-Моралес Бальтасар (1601-1658),
іспанський філософ.
- Розкладіть многочлен на множники
1.1.
|
а)
б)
в)
г)
д) |
е)
є)
ж)
з)
и) |
1.2.
1) ![]() ; 3)
; 3) ![]() ;
;
2) ![]() ; 4)
; 4) ![]()
2. Доведіть тотожність
2.1. ![]() .
.
2.2. ![]()
2.3. ![]() .
.
2.4. ![]() .
.
3. Розв’яжіть рівняння
3.1. ![]() .
.
3.2. ![]()
3.3. ![]()
3.4. ![]()
3.5.![]()
3.6. ![]()
3.7. ![]()
3.8. ![]()
3.9. ![]()
4. Побудуйте математичну модель і розв’яжіть задачу:
4.1. Автомобіліст виїхав з міста на дачу по дорозі, довжина якої 24 км, а повернувся додому іншою дорогою, довжиною 30 км. Збільшивши на зворотному шляху швидкість на 2 км /год., він проте витратив на зворотний шлях на 6 хв. більше, ніж на шлях на дачу. З якою швидкістю автомобіліст їхав на дачу, якщо відомо, що його швидкість була більшою за 20 км /год.?
4.2. Моторний човен проплив за течією річки 18 км, а потім проти течії - 30 км. При цьому на весь шлях він затратив 8 год. Знайдіть власну швидкість човна, якщо швидкість течії річки дорівнює 2 км/год.
4.3. Теплохід проплив 9 км по озеру і 20 км за течією річки за 1 годину. Чому дорівнює власна швидкість теплоходу, якщо швидкість течії річки дорівнює 3 км/год.?
4.4. Два автобуси вийшли одночасно з пункту А в пункт В, відстань між якими 48 км. Швидкість першого автобуса була на 4 км/год. більшою, і тому він прибув в пункт В на 10 хвилин раніше. Знайдіть швидкість другого автобуса.
4.5. З пункту А виїхав велосипедист, а через 45 хв. після цього в тому ж напрямку виїхала вантажівка, яка наздогнала велосипедиста на відстані 15 км від пункту А. Знайдіть швидкість велосипедиста і швидкість вантажівки, якщо швидкість вантажівки на 18 км/год. більша за швидкість велосипедиста.
4.6. За течією річки від пристані відійшов пліт. Через 4 години від цієї пристані в тому ж напрямку відійшов човен, який наздогнав пліт на відстані 15 км від пристані. Знайдіть швидкість течії, якщо власна швидкість човна становить 12 км/год.
4.7. Човен проплив 15 км за течією річки і повернувся назад, витративши на зворотний шлях на 1 год. більше. Знайдіть швидкість човна за течією річки, якщо швидкість течії річки становить
2 км/год.
4.8. Спочатку траншею рила перша бригада робітників. Через 4 години до неї приєдналась друга бригада, і, пропрацювавши разом ще 8 годин, вони вирили траншею повністю. За скільки годин вирила б цю траншею друга бригада, працюючи самостійно, якщо першій бригаді треба було б на це на 8 годин більше?
4.9. Перший робітник, працюючи самостійно, може виконати замовлення на 3 години швидше, ніж другий. За скільки годин виконає це замовлення один другий робітник, якщо разом вони його виконали за 2 години?
4.10. Майстер і його учень можуть виконати, працюючи разом, деяку роботу за 3 години. Скільки часу необхідно учневі, щоб виконати цю роботу самостійно, якщо відомо, що майстер, працюючи один, зможе виконати її на 8 годин швидше?
4.11. Два насоса, працюючи одночасно, можуть наповнити порожній басейн за 6 годин. При цьому один перший насос наповнить цей басейн на 9 годин швидше, ніж другий, працюючи самостійно. Скільки годин знадобиться другому насосу, щоб наповнити цей басейн?
4.12. У сплав міді і цинку, що містить 60 кг міді, додали 160 кг цинку. У результаті процентний вміст міді в сплаві зменшився на 10. Чому дорівнювала початкова маса сплаву ?
4.13. У сплав міді та олова, що містить 5 кг олова, додали 15 кг міді. В результаті процентний вміст міді в сплаві збільшився на 30. Скільки кілограмів міді було в початковому сплаві?
4.14. До розчину, який містить 20 г солі, додали 100 г води, після чого концентрація солі зменшилася на 10 %. Скільки грамів води містив розчин спочатку?
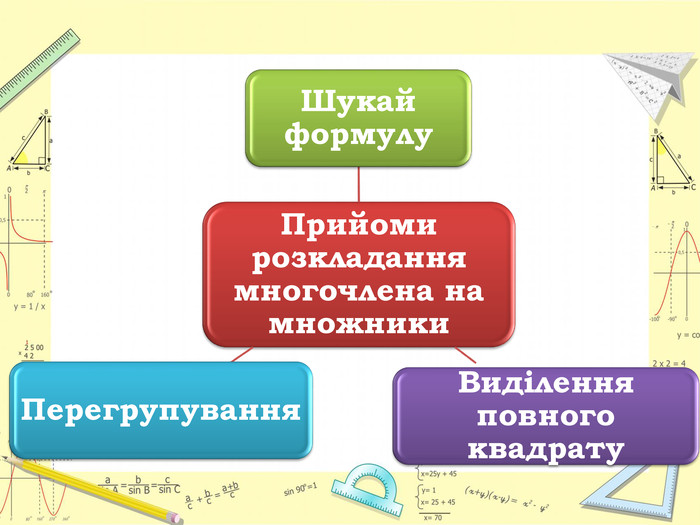
Практичні поради
Найчастіше для розкладання многочлена на множники потрібне використання всіляких комбінацій різних способів.
Розглянемо приклади, в яких для розкладання многочлена на множники потрібно застосувати кілька різних способів.
Приклад 1. Розкладіть на множники многочлен
а4 + ах2 ![]()
Вироблення стратегії розв’язання.
Так як а4 = ( а2 )2, а х4 = ( х2 )2, то, згрупувавши перший та четвертий доданки, ми зможемо застосувати формулу різниці квадратів:
а4 ![]()
![]()
![]()
![]()
![]()
(а2 ![]()
![]()
![]()
![]()
а4 ![]()
![]()
![]()
Тепер згрупуємо другий і третій доданки, які мають спільний множник ах. Після винесення його за дужки в дужках залишиться многочлен х ![]()
![]()
![]()
ах2 ![]()
![]()
![]()
Таким чином, в результаті проведених перетворень обидві групи доданків будуть мати спільний множник а ![]()
Реалізація стратегії.
Проведемо зазначене групування. Як і планували, в першій групі застосуємо формулу різниці квадратів, а в другій - винесемо за дужки спільний множник ах :
![]()
![]() а4 + ах2
а4 + ах2 ![]()
![]()
![]()
![]()
![]()
![]()
![]()
= ( а ![]()
![]()
Запишемо вираз у квадратних дужках як многочлен стандартного вигляду:
( а + х ) (а2 ![]()
![]()
![]()
У результаті отримуємо таке розкладання даного многочлена на множники:
а4 + ах2 ![]()
![]()
![]()
Приклад 2. Розкладіть на множники многочлен
х4 + х2 у + ху3 + 2ху2 + у3 .
Вироблення стратегії розв’язання.
Помічаємо, що серед членів нашого многочлена є одночлен 2ху2. Цей доданок є подвоєним добутком х і у2. Якби у нас були також доданки х2і у4, то, згрупувавши їх, ми змогли б застосувати формулу квадрата суми. Але таких доданків у нас немає.
Однак, аналізуючи даний многочлен, можна помітити, що в групі х2 у + 2ху2 + у3, що складається з другого, четвертого і п'ятого доданків, ми можемо винести за дужки спільний множник у. А в дужках опиниться квадрат суми х і у. Таким чином,
х2 у + 2ху2 + у3 = у (х2 + 2ху + у2) = у (х + у) 2 .
Перший і третій доданки мають спільний множник х. Якщо ми винесемо його за дужки, то в дужках залишиться сума кубів х і у. Застосовуючи відповідну формулу, отримаємо
х4+ ху3 = х (х3+ у3) = х ( х + у) ( х2 ![]()
Таким чином, кожна з груп буде мати спільний множник х + у, який можна винести за дужки.
Реалізація стратегії.
Об'єднаємо перший і третій члени даного многочлена в одну групу, а другий, четвертий і п'ятий - в іншу і винесемо в кожній групі за дужки спільний множник:
х4 + х2 у + ху3 + 2ху2 + у3 = (х4 + ху3) + (х2 у + 2ху2 + у3) = х (х3+ у3) + + у (х2 + 2ху + у2).
Тепер в першому доданку застосуємо формулу суми кубів, а в другому - формулу квадрата суми. Тоді в кожній групі утворюється спільний множник х + у, який можна винести за дужки:
х ( х + у) ( х2 ![]()
![]()
Перетворюючи потім вираз у квадратних дужках, отримуємо:
х ( х2 ![]()
![]()
Таким чином, ми приходимо до наступного розкладання даного многочлена на множники:
х4 + х2 у + ху3 + 2ху2 + у3 = ( х + у) [х3 ![]()
Приклад 3. Розкладіть на множники многочлен х4 + 4 .
Вироблення стратегії розв’язання.
Помічаємо, що даний вираз ми можемо записати у вигляді ( х 2) 2 + + 22. Таким чином, даний вираз є сумою квадратів. Але формули для суми квадратів у нас немає, тому відразу розкласти многочлен на множники нам не вдасться.
Можна зауважити також, що х4 + 4х2 + 4 = ( х2 + 2 )2. А значить, якщо ми додамо і віднімемо від даного многочлена одночлен 4х2, то отримаємо:
х4 + 4 = х4 + 4х2 + 4 ![]()
![]()
А отриманий вираз ми вже зможемо розкласти на множники, використовуючи формулу різниці квадратів.
Реалізація стратегії.
Як і планували, додамо до даного многочлену і віднімемо від нього![]()
х4 + 4 = х4 + 4 + 4х2 ![]()
![]()
![]()
= ( х2 + 2 )2![]()
![]()
![]()
![]()
![]()
У результаті ми приходимо до наступного розкладання даного многочлена на множники:
х4 + 4 = (х2 ![]()
![]()
Приклад 4. Розкладіть на множники многочлен: х3 + 6х2 + 11х + 6.
Вироблення стратегії розв’язання.
Зауважимо, що в останніх трьох доданках, якщо додати до них х і винести за дужки 6, «захована» формула квадрата суми ( х + 1) 2.
Щоб вираз при цих перетвореннях не змінився, від нього треба відняти х. Тоді невикористані доданки утворюють групу х3 ![]()
![]()
![]()
Таким чином, в кожній з утворених двох груп маємо множник х + 1, який можна винести за дужки.
Реалізація стратегії.
Провівши зазначені перетворення, отримаємо:
х3 + 6х2 + 11х + 6 = х3 + 6х2 + 12х + 6 ![]()
![]()
![]()
![]()
![]()
Перетворимо вираз у квадратних дужках. Для цього спочатку спростимо його, а потім доданок 5х представимо у вигляді двох доданків 2х і 3х:
х ( х ![]()
![]()
![]()
![]()
= х ( х + 2 ) + 3 ( х + 2 ) = ( х + 2 ) ( х + 3 ).
У результаті ми отримуємо таке розкладання даного многочлена на множники :
х3 + 6х2 + 11х + 6 = ( х + 1 ) ( х + 2 ) ( х + 3 ).
Приклад 5. Розкладіть на множники многочлен х2 + 0,5 х ![]()
Вироблення стратегії розв’язання.
Розкладемо цей многочлен на множники способом виділення повного квадрата, який часто використовується при розкладанні на множники багатьох тричленів.
Для цього зауважимо, що доданок 0,5 х можна записати як подвоєний добуток х і числа ![]() . Тепер, додаючи і віднімаючи від даного многочлена
. Тепер, додаючи і віднімаючи від даного многочлена ![]() (квадрат числа
(квадрат числа ![]() ) виділяємо повний квадрат. Після цього для розкладання многочлена на множники використовуємо формулу різниці квадратів.
) виділяємо повний квадрат. Після цього для розкладання многочлена на множники використовуємо формулу різниці квадратів.
Реалізація стратегії.
Виконуючи вищесказане, отримуємо
х2 + 0,5 х ![]()
![]() +
+ ![]() 3 = (х2 + 2· х ·
3 = (х2 + 2· х ·![]() +
+ ![]() =
=
= (х + ![]() )2
)2 ![]()
![]() = (х +
= (х + ![]() +
+ ![]() )( х +
)( х + ![]()
![]() ) = (х + 2 )( (х
) = (х + 2 )( (х ![]()
Отже, розкладання на множники даного тричлена має вигляд:
х2 + 0,5 х ![]()
![]()
«Заперечувати за математичними формулами
об'єктивну реальність - це значить не бачити за деревами лісу».
Людвіг Больцман (1844-1906),
австрійський фізик-теоретик.
Задача 1. Задумали три раціональних числа. Добуток першого і третього з них дорівнює (![]()
Побудова математичної моделі.
Нехай перше раціональне число дорівнює х. Тоді друге раціональне число дорівнює х + 6 , а третє дорівнює х ( х + 6 ) + 11. Відомо, що х [х ( х + 6 ) + 11 ] = ![]()
Складемо математичну модель задачі:
![]()
![]()
![]()
Стратегія розв’язання рівняння.
Для того щоб розв’язати дане рівняння, запишемо його у вигляді
х [х ( х + 6 ) + 11 ] + 6 = 0
і розкладемо многочлен в лівій його частині на множники. Потім прирівняємо кожен з множників до нуля і знайдемо корені одержаних рівнянь. Тим самим ми знайдемо корені даного рівняння, так як добуток дорівнює нулю тоді і тільки тоді, коли хоча б один із множників дорівнює нулю.
Отже, для вирішення завдання виконаємо наступні дії в такій послідовності:
Крок 1. Представимо рівняння х [х ( х + 6 ) + 11 ] = ![]()
х [х ( х + 6 ) + 11 ] + 6 = 0 і запишемо його ліву частину як многочлен стандартного вигляду.
Крок 2. Розкладемо отриманий многочлен на множники.
Крок 3. Кожен з множників прирівняємо до нуля і знайдемо корені отриманих рівнянь.
Крок 4. Перевіримо, що корені рівнянь є раціональними числами.
Крок 5. Обчислимо х + 6 , х ( х + 6 ) + 11 і запишемо відповідь.
Реалізація стратегії.
Крок 1
х [ х ( х + 6 ) + 11 ] = ![]()
<=> х3+ 6х2 + 11х + 6 = 0
Крок 2
Проводимо необхідні перетворення:
х3+ 6х2 + 11х + 6 = х3+ 6х2 + 12х + 6 ![]()
![]()
= х ( х + 1 ) ( х ![]()
![]()
= ( х +1) · ( х2 + 5х + 6 ) = ( х + 1 ) ( х + 2 ) ( х + 3 ).
Крок 3
Рівняння ( х + 1 ) ( х + 2 ) ( х + 3 ) = 0 рівносильне даному. Щоб його розв’язати, прирівняємо до нуля кожен з множників:
( х + 1 ) ( х + 2 ) ( х + 3 ) = 0
х + 1 = 0 або х + 2 = 0 або х + 3 = 0
х = ![]()
![]()
![]()
Таким чином, ми отримали, що корені даного рівняння є числа ( ![]()
![]()
![]()
Крок 4
Всі отримані розв’язки є раціональними числами.
Крок 5
Якщо х = ![]()
х + 6 = ![]()
![]()
Якщо х = ![]()
х + 6 = ![]()
![]()
Якщо х = ![]()
х + 6 = ![]()
![]()
Відповідь: могли задумати такі трійки раціональних чисел: (![]()
![]()
(![]()
Задача 2. Ширина прямокутника на 5 см менша від сторони квадрата, а його довжина - на 3 см більша сторони цього ж квадрата. Знайдіть довжину даного прямокутника, якщо його площа дорівнює 9 см2.
Побудова математичної моделі.
Нехай сторона квадрата дорівнює х см, де х > 0.
Тоді ширина прямокутника дорівнює (х ![]()
![]()
Нам відомо, що площа прямокутника дорівнює добутку його довжини і ширини. З іншого боку, за умовою задачі вона дорівнює 9 см2.
Складемо математичну модель задачі:
![]()
![]()
![]()
Стратегія розв’язання рівняння.
Для відповіді на запитання задачі нам треба розв’язати рівняння
![]() . Загальний спосіб розв’язання таких рівнянь нам поки не відомий.
. Загальний спосіб розв’язання таких рівнянь нам поки не відомий.
Але нам зустрічалися рівняння виду ( ах + b) (сх + d ) = 0, де { а, b, с, d } ![]()
( ах + b) (сх + d ) = 0 ![]()
А знаходити розв’язки таких рівнянь ми вже вміємо. Тим самим розв’язання рівняння невідомого виду буде нами зведено до розв’язання уже відомих рівнянь.
Таким чином, для розв’язання задачі нам треба виконати наступну послідовність дій.
Крок 1. Представимо рівняння ( х ![]()
( х ![]()
![]()
Крок 2. Розкладемо отриманий многочлен на множники.
Крок 3. Кожен з множників прирівняємо до нуля і знайдемо корені отриманих рівнянь.
Крок 4. Виберемо з усіх коренів ті, які задовольняють нерівностям х > 0 , х ![]()
Крок 5. Для обраних коренів обчислимо х + 3 і запишемо отриману відповідь.
Реалізація стратегії.
Крок 1
( х ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Крок 2
Для того щоб розкласти многочлен х2 ![]()
![]()
х2 ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
(х ![]()
![]()
![]()
![]()
![]()
![]()
Крок 3
Щоб розв'язати рівняння ( х ![]()
![]()
( х ![]()
![]()
![]()
![]()
![]()
Корені х = 6 і х = ![]()
![]()
Крок 4
Корінь х = 6 задовольняє всім трьом даними нерівностям, так як 6 > 0, 6![]()
Корінь х = ![]()
![]()
Крок 5
Обчислимо шукане значення довжини прямокутника:
х +3 = 6 +3 = 9 ( см).
Відповідь: довжина прямокутника дорівнює 9 см.
Завдання на кмітливість
На контрольній роботі з математики потрібно було розв’язати рівняння х3 + х = 2х2.
Юрко розв’язував це рівняння таким чином:
«Помітивши, що многочлен в правій частині рівняння має спільний множник х, він виніс його за дужки. Потім він розділив праву і ліву частини на одне і те ж число х і отримав рівняння х2 + 1 = 2х. Після цього він додав до правої і лівої частини рівняння одне і те ж число ( ![]()
х3 + х = 2х2 ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
<=> х = 1.
Сашко ж розв’язував це рівняння інакше:
«Він спочатку додав до правої і лівої частини рівняння одне і те ж число (![]()
х3 + х = 2х2 <=> х3 + х ![]()
![]()
<=> х (х ![]()
![]()
![]()
![]()
![]()
х = 0 <=> х = 1 або х = 0.
Чому хлопчики отримали різні відповіді? У якому місці і ким з них була допущена помилка? Яке правило було порушено і як правильно розв’язати дане рівняння?


про публікацію авторської розробки
Додати розробку