урок з геометрії для 11 класу

Державний професійно-технічний навчальній заклад

Херсонський професійний ліцей зв’язку та поліграфії

 

 

 

 

 

 

 

 

 

 

Методична розробка уроку з

геометрії

 

за темою:

«Тіла обертання. Об'єми та площі поверхонь»

 

 

 

 

 

 

Розроблено викладачем

математики

Свідер Л. М.

 

 

 

 

 

 

 

 

 

 

 

Херсон – 2019

ПРЕДМЕТ «Геометрія»

 

 

 

Дата проведення ________                                                    група _______

 

Тема програми: Тіла обертання

 

Тема уроку: Тіла обертання. Об'єми та площі поверхонь

 

Мета уроку: узагальнити і систематизувати знання учнів з теми, показати практичне застосування вивчених формул, за якими знаходяться об'єми та площі поверхонь тіл обертання, звернути увагу учнів на зв'язок предмета з життям; розширити кругозір учнів та їхню просторову уяву; вчити орієнтуватися в нестандартних ситуаціях.

Розвивати самостійне логічне мислення, уміння і навички практичного застосування одержаних знань; удосконалювати  досвід колективної роботи для підвищення успішності та відповідальності; розвивати здібності пошукового характеру.

Формувати елементи колективізму при розв'язанні задач практичного характеру. Виховувати взаємоповагу, доброзичливість між учнями та викладачем. Виховувати відповідальність, працелюбність, чесність, принциповість у відношенні до себе і до всіх членів колективу групи.

 

Тип уроку: систематизації та узагальнення знань з елементами інтерактивного навчання.

 

Методи навчання, прийоми: інтерактивні прийоми, групова та індивідуальна робота учнів, самостійна робота, проблемні питання, практична робота, елементи самоконтролю.

 

Основні терміни і поняття: тіла обертання, циліндр, конус, куля, твірна, основа, переріз, вісь, об’єм, площа поверхні.

 

Міжпредметні зв’язки: література, економіка, фізика, інформатика.

 

Наочність: моделі тіл обертання, картки.

 

Технічні засоби навчання: комп`ютер, мультимедійна система, комп’ютерні презентації.

 

 

 

 

Хід уроку

 

1. Організаційний момент.

 

2. Мотивація навчальної діяльності.

 

Повідомлення теми і мети уроку.

Викладач. Сьогодні в нас відбудеться презентація товарів «Тіла обертання». До нас завітали представники різних фірм, акціонерних товариств, які представляють нам свою продукцію. Вони хочуть переконати всіх присутніх, що саме їх товар – гарант вашого благополуччя.  Фірми, безумовно, конкурують між собою, а тому підготовка презентації велась таємно. Отже, під час представлення товару, представники інших фірм мають право задавати запитання конкурентам. Фірми конкурують в боротьбі за право отримання сертифікатів якості:

1. Краще представлення товару;
2. Краща практична задача;
3. Краще запитання до пояснення.
4. Краще виконання математичного диктанту.
5. Краща самостійна робота.

 

ІІІ. Повторення і узагальнення понять і засвоєння відповідної їм системи    знань.

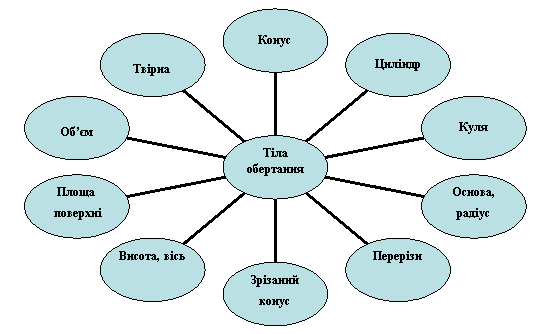
1. Вправа «Асоціативний кущ». Перевіримо готовність фірм до презентації. В центрі дошки вчитель пише слова «Тіла обертання і пропонує учням згадати слово чи словосполучення, які асоціюються з цими словами

 

2. Вправа «Мікрофон». На дошку проектуються формули для обчислення об’ємів та площ поверхонь тіл обертання. Учні відповідають , що можна знайти за допомогою даних формул.

– площа сфери;

- площа бічної поверхні конуса;

– площа бічної поверхні циліндра

– об'єм циліндра;

– об’єм конуса;

– об’єм кулі.

IV. Приведення одиничних знань у  систему.

1. Представлення презентацій фірмами.

Фірма «Куля»

1. Реклама товару фірми.

 

 

2. Постачальники спортінвентаря.

Задача. Скільки потрібно квадратних сантиметрів шкіри, щоб зробити 

покришку для футбольного м'яча? (На шви і обрізки додати 5% матеріалу).

Розв'язання:

Діаметр футбольного м’яча стандартний – він дорівнює 25 см.

;     ;

;     

Обчислимо 5% від даної площі S₁=0,196  0,05 = 0,0098 (м²).

Отже, всього потрібно матеріалу: 0,196 + 0,0098 = 0,206 (м²).

Відповідь: 2060 см².

Фірма «Циліндр»

1. Реклама товару фірми.

2. Постачальники труб.

Задача. Циліндрична димова труба діаметром 65 см має висоту 18 м. Скільки жерсті потрібно для її виготовлення, якщо на з’єднання іде 10% матеріалу?

Розв’язання:

d = 65см =0,65м; H = 18м.

S = 2RH = dH;

S = 3,14  0,65 18  36,74 (м²);

Знайдемо 10%від знайденої площі S₁ = 36,74  0,1 = 3,67 (м²).

Отже, всього необхідно  матеріалу 36,74 +3,67 = 40,4(м²).

Відповідь: 40,4 м².

Акціонерне товариство «Конус»

1. Реклама товару товариства.

 

2. Промислові виробники.

Задача. Конусоподібний намет висотою 3,5 м і діаметром основи 4м покрито тканиною. Скільки тканини пішло на намет?

Розвязання:

H = 3,5м, d = 4м, тому R = 2м.

S = Rl;l² = H² + R² = 2² + 3,5² = 16,25;

l = 4,02 (м).

Отже, S = 3,14  4,02  2  25,3 (м²).

Відповідь: 25,3(м²).

 

2 . Математичний диктант у вигляді гри «Розшифруй вислів». (Кожній цифрі відповідає перша буква правильної відповіді) – правильно розшифрований вислів – 1 бал представникам однієї із фірм.

 

1	2	3	4	5	6	7		8	9	10	11	12
У	К	Р	А	Ї	Н	А		Є	Д	И	Н	А

 

У) 1. Підготувалися до відкритого. (Уроку).

К) 2. Ця фігура відноситься до тіл обертання. Її осьовий переріз – трикутник. Що це за фігура? (Конус).

Р) 3. Відрізок, що сполучає центр кола з точкою кола. (Радіус).

А) 4,7,12. Висота бічної гранні правильної піраміди, проведеної з її вершини. (Апофема).

Ї) 5. Він гуляє серед ночі.

       Певно добрі має очі.

       Одяг весь із колючок

       Це безстрашний …(Їжачок).

Н) 6,11. У звичайного конуса дві основи? (Ні).

Є) 8. Прямокутний трикутник зі сторонами 3, 4, 5 одиниць називається … (Єгипетським).

Д) 9. Відрізок, що сполучає дві точки кола і проходить центр кола. (Діаметр).

И) 10.

3. Тестові завдання.

Знайди правильну відповідь

	R	H	V
Циліндр	8	6	а) 384; зелений. б) 384 ; синій. в) 186 . жовтий.
Конус	3	10	а) 90 ; зелений. б) 30; синій в) 30 ; жовтий.

 

4. Самостійна робота за принципом контролю і самоконтролю (кожному учню по два аркуша)  у  вигляді гри «Перевір себе»  (правильна відповідь – 1 бал представникам однієї з фірм).

 

«Перевір себе»

А	Рівнобедрений трикутник	ПRL	ПR2
В	Вісь		Діаметр	прямокутний трикутник
С	2ПRH + 2ПR2			2ПRH
	1	2	3	4

 

Питання:

1. Тіло, що утворене двома кругами, що лежать у паралельних площинах і усіма відрізками, що з’єднують відповідні точки цих кругів.
2. Бічна поверхня циліндра.
3. Переріз конуса площиною, що проходить через вісь.
4. Хорда, що проходить через центр основи конуса.
5. Тіло, утворене  кругом, точкою поза його площиною і усіма відрізками, що з’єднують цю точку з точками круга.
6. Переріз циліндра площиною, паралельною його основам.
7. Пряма, що проходить через висоту конуса.
8. Бічна поверхня конуса.
9. Фігура, при обертанні якої описується конус.
10. Площа повної поверхні циліндра.
11. Площа основи конуса.
12. Фігура, при обертанні якої описується циліндр.

 

Відповіді: В2 С4

3.А1 4. В3 5.С3

6. С2 7. В1 8. А2

9. В4 10.С1 11. А3

12. А4

 

V. Підбиття підсумків уроку. Рефлексія.

1.Вчитель: Минають роки… геометрія збагачується новими фактами, змінює свій вигляд. Були часи, коли вона, як при Платоні або Піфагорі, займала становище справжньої цариці наук, а були й періоди, коли вона в своєму розвитку починали відставати від інших, молодих, що бурхливо  розвивалися, наук. Але ніколи, очевидно, поки стоїть світ, не настане такий час, коли людство могло  сказати: «Ось тепер геометрія не потрібна і залишається здати її в архів.»

Геометрія була і буде постійною супутницею людини на всьому шляху її розвитку, у всій її довгій, складній і цікавій еволюції.

Отже, як ми бачили, застосування математики в усіх галузях науки, господарства і життя необмежене. Математика скрізь, вона – на кожному кроці.

Наше суспільство потребує, як талановитих дослідників, так і спеціалістів, які добре знають математику та здатні застосовувати свої знання на практиці.

Де ж практично використовуються знання про тіла обертання, обчислення їх об’ємів та площ поверхонь:

• архітектура;
• будівництво;
• сільське господарство;
• промисловість;
• наука;
• космонавтика.

 

2.Оцінки учням: визначення  та присудження сертифікатів якості та кращу презентацію, кращу практичну задачу та краще запитання до пояснення задачі.

 

VI. Інформація – інструктаж домашнього завдання.

 

Вчитель: Як результат презентації є нові адреси, нові пропозиції, які отримують наші фірми для розширення своєї сфери діяльності. Домашнє завдання, яке надійшло до факсу, отримує кожна група:

Задача 1. Нехай  у нас є дві циліндричні каструлі: одна вузька і висока, а друга вдвоє нижча, але вдвоє ширша. Яка з каструль матиме більшу місткість?

Задача 2. Продаються два кавуни кулястої форми: один – в півтора рази ширший, ніж другий, і вдвоє дорожчий. Який кавун вигідніше купити?

Задача 3. Припустимо, що земну кулю охоплено по екватору обручем, довжина якого перевищує довжину екватора на 10 метрів, причому обруч скрізь однаково віддалений від поверхні Землі. Який завбільшки проміжок між земною поверхнею і обручем? Чи змогла б пролізти під обручем миша?

Задача – жарт. Чому ковбасу нарізають косо, а не прямо?