Урок з медіа-презентацією. "Комбінаторні задачі"

Тема уроку.                               Комбінаторні задачі.

Мета уроку: узагальнити і систематизувати знання учнів з теми «Комбінаторика. Розв’язування комбінаторних задач»;

                       розвивати логічне мислення, пам’ять, творчу активність,  уміння і навички необхідні для розв’язування комбінаторних задач, формувати вміння аналізувати і робити висновки, здатність швидко адаптуватись в нестандартних умовах; 

                      виховувати вміння колективно працювати, боротись за перемогу,культуру мовлення і поведінки з суперниками, прищеплювати любов до математики.

Тип уроку: узагальнення і систематизація знань, умінь і навичок.

Обладнання: медіа проектор, презентація «Морський бій».

Урок проходить за відомими всім правилами гри «Морський бій». Клас заздалегідь поділено на три команди. Кожна команда повинна обрати собі назву і девіз. Вчитель вибирає собі двох або трьох помічників (журі), як правило з числа кращих учнів, які слідкують за правильністю і швидкістю виконання завдань.

Будь-яка красиво розв’язана  математична задача приносить розумове задоволення, а будь-яке зосереджене міркування заспокоює серце та робить його співзвучним Всесвіту.                                  Герман Гессе

Хід уроку

1. Організаційний момент

Перевірка готовності учнів, класу до уроку.

2. Перевірка домашнього завдання

З метою економії часу перевірці і аналізу підлягають тільки ті завдання, які викликали труднощі під час виконання, якщо таких завдань не виявлено переходимо до наступного етапу уроку.

3. Мотивація навчальної діяльності

З задачами, в яких приходиться вибирати ті чи інші предмети, розміщувати їх в певному порядку і відшуковувати серед різних розміщень найкращі, люди стикнулися ще в доісторичну епоху, обираючи найкращі розміщення мисливців під час полювання, воїнів під час битви, інструментів під час роботи. Пізніше, поряд із спортивними змаганнями з’явились ігри з різними фігурами чи предметами, в яких вигравав той, хто краще знав переможні комбінації та вмів уникати програшних. Комбінаторика – важливий розділ математики, знання якого необхідно представникам різноманітних спеціальностей. З комбінаторними задачами доводиться мати справу фізикам, хімікам, біологам, лінгвістам, спеціалістам по кодам та ін.. Комбінаторні методи лежать в основі рішення багатьох задач теорії ймовірностей та її застосувань. Комбінаторика – гілка математики, що вивчає комбінації та перестановки предметів, – виникла в XVII ст. Довгий час здавалося, що комбінаторика лежить позамежами основної течії розквіту математики. Зараз комбінаторні методи застосовуються в теорії випадкових процесів, статистиці, математичному програмуванні, обчислювальній математиці, плануванні експериментів, і т.п. В математиці комбінаторика використовується при вивченні комбінаторної геометрії, представлень груп, неасоціативних алгебри і т.д.

  Що ж було поштовхом до виникнення  комбінаторики, як науки? Для чого ще потрібні знання з комбінаторики, крім відомого вже нам застосування в теорії ймовірності?

Доповіді  учнів

 Під час доповідей на екрані з’являються портрети вчених-математиків.

1.Перша праця, що містила комбінаторні задачі, увійшла в книгу «Книгу Абака» видатного математика Леонардо Фібоначчі в 1202 р. Наприклад, задача про пошук найменшої кількості гир, за допомогою яких можна отримати будь-яку цілу вагу від 1 до 40 фунтів.

      Але поштовхом до виникнення комбінаторики був розквіт азартних ігор, зокрема гри в кості. Питаннями, що пов’язані з цією грою, займалися в ХVIст. італійські математики – Джероламо Кардано, Н. Тарталья, в ХVIІст. – Галілео Галілей, видатні математики Франції – Блез Паскаль і П’єр Ферма. Саме роботи Паскаля і Ферма дали поштовх  для народження нових гілок математичної науки – комбінаторики і теорії імовірності. Вже у 1666 р. Готтфрід Вільгельм Лейбніц публікує «Дисертацію про комбінаторне мистецтво, в котрій вперше з’являється сам термін «комбінаторика». Лейбніц, якому на той час було всього 20 років і котрий мав вчений степінь з юриспруденції, планував для комбінаторики нові додатки: до кодування, статистики, теорії спостережень. Учень Лейбніца – Якоб Бернуллі в своїй книзі «Мистецтво припущень» (1713р.) виклав багато відомостей з комбінаторики та вперше увів поняття «перестановки», «розміщення». Остаточно комбінаторика як самостійний розділ математики оформилась в працях Леонардо Ейлера у ХVIІІст.

            2.Для кодування таємної інформації та її розшифровки потрібні знання комбінаторики, тому для вирішення цих питань залучали математиків. Першим дешифрувальником був «батько алгебри» –  Франсуа Вієт (кінець  ХVIст.).  Навички в розгадці складних шифрів допомогли вченим, коли археологи почали відкопувати камені та інші предмети давнини з таємними знаками. Таким чином і в археології комбінаторика має застосування.

 Складність будови біологічних систем, взаємне поєднання окремих процесів в цілому організмі роблять біологію зручним полем застосування комбінаторних методів. Поєднуючи їх з вивченням рентгенівських знімків, вченим вдалося розгадати будову багатьох білків, в тому числі гемоглобіну та інсуліну. Найбільшим досягненням комбінаторного підходу до проявів життя можна вважати розшифровку будови ДНК, зроблену в Кембриджі вченими Ф. Криком та Дж. Уотсоном у 1953 р.

Комбінаторика виявилась корисною і в хімії. Розкладуючи свій хімічний пасьянс, великий вчений Дмитро Іванович Мендєлєєв, знайшов правильне розміщення елементів, виникла таблиця – був відкритий періодичний закон.(17 лютого 1869р.). У фізиці комбінаторика виявляється необхідною при вивченні властивостей кристалів, опису моделі феромагнетизму та ін..

4. Актуалізація опорних знань

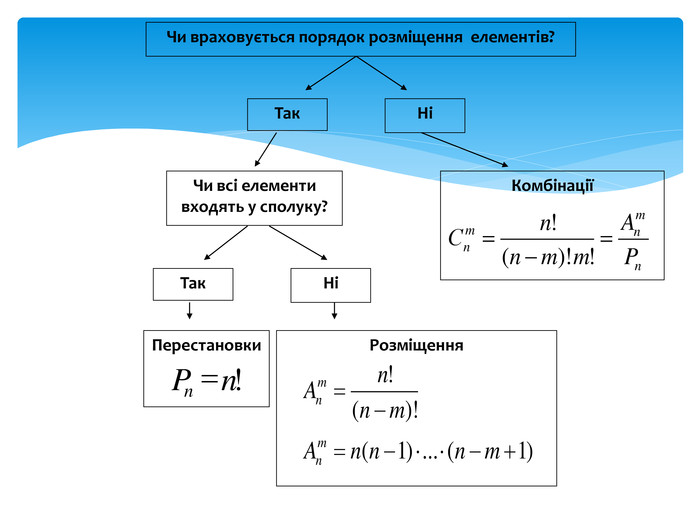
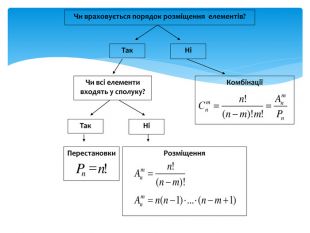
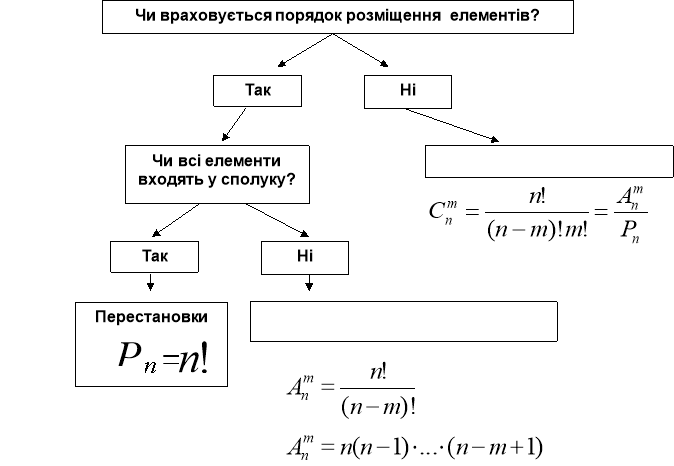
Слово вчителя.  Ми вже розв’язували з Вами  комбінаторні задачі, але здебільшого знали, який вид сполук в них присутній, або яке правило: суми чи добутку треба застосувати. Тепер  Вам потрібно навчитися самостійно розрізняти види сполук в комбінаторних задачах. Для цього пригадаємо схему розв’язування комбінаторних задач. (Схема проектується на екран)

5. Перший конкурс «Привітання»

Команди оголошують назву і девіз. Журі оцінює. Максимальна оцінка – 10 балів.

6.         Другий конкурс «Математичний морський бій»

Правила гри . На екрані з’являється таблиця в якій зашифровано математичний термін.

Задача гравців – якомога швидше його відгадати.

Можливі такі чотири варіанти:

Перший варіант

Учні бачать цифру 5. Це означає, що команда отримує завдання на 5 балів, на яке треба відповісти без підготовки. У випадку правильної відповіді команда отримує 5 балів.

Другий варіант

Учні бачать цифру 10. Це означає, що команда отримує завдання на 10 балів. На виконання якого відводиться 3 хвилини. У разі правильної відповіді команда отримує 10 балів.

Третій варіант

Учні бачать цифру 15 і отримують завдання на 15 балів, на виконання якого відводиться 5 хвилин. У разі правильної відповіді команда отримує 15 балів.

Четвертий варіант

Учні бачать букву зашифрованого слова. Балів у цьому випадку команда не отримує, але може назвати дане слово. У разі, якщо назване слово правильне, команда отримує у свою скарбницю 20 балів і гра припиняється. Журі підраховує кількість балів набраних командами і оголошує переможця.

Зауваження до правил

1. Завдання виконують усі три команди. У випадку, якщо команда не має відповіді на питання, на нього має право відповісти та команда, капітан якої перший піднесе руку.
2. Команди «стріляють» по черзі за годинниковою стрілкою незалежно від того правильно чи ні вони відповіли на попереднє питання.
3. Слово для відповіді має тільки капітан команди або той, кого він призначить.
4. У випадку  коли жодна з команд не справляється із завданням його пояснює вчитель, але з кожної команди знімають по 10 балів.

Повністю розшифрована таблиця має вигляд:

Зашифроване слово «АБСЦИСА».

Завдання на 5 балів

1. Обчислити .

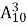Розв’язання

=109∙8=720.

Відповідь: 720.

2. Обчислити 5!.

Розв’язання

 5!=1∙2∙3∙4∙5=120.

Відповідь: 120.

3. Що називають перестановкою? Формула для обчислення числа перестановок.

Відповідь: перестановкою скінченної множини М називають будь-яку упорядковану множину, утворену з усіх елементів множини М.  =n!

4. Що називають розміщенням з n елементів по m? За якою формулою обчислюють?

Відповідь: будь-яку m-елементну впорядковану підмножину даної n-елементної множини (m≤n) називають розміщенням з n елементів по m.

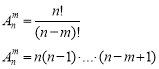
5. Що називають комбінацією з n елементів по m? За якою формулою обчислюють?

Відповідь:  будь-яку m-елементну  підмножину даної n-елементної множини (m≤n) називають комбінацією з n елементів по m.

= .

6. Що називають факторіалом натурального числа n?

Відповідь: факторіал натурального числа n — добуток натуральних чисел від одиниці до n включно, позначається n!. За означенням 0!=1.

7. Обчислити .

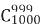Розв’язання

===1000.

Відповідь: 1000.

8. У їдальні три перших, п’ять других і дві треті страви. Скількома способами можна скласти з них обід, який містить всі три страви?

Розв’язання

Першу страву можна вибрати трьома способами, другу - п’ятьма, третю – двома способами. Застосувавши правило добутку маємо 3∙5∙2=30 способів.

Відповідь: 30 способів.

9. Скільки двоцифрових чисел можна скласти з цифр 1,2,3,4,5,6?  Цифри в числі можуть повторюватись.

Розв’язання

Першу цифру можна вибрати 6 способами, другу теж 6 способами. Застосувавши правило добутку маємо 6∙6=36 способів скласти двоцифрове число.

Відповідь: 36способів.

10.  Скількома способами можна розставити  7 книжок на полиці?

Розв’язання

.

Відповідь: 5040 способів.

Завдання на 10 балів

1. Обчислити .

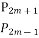Відповідь:2m(2m+1).

2.  Скільки трицифрових чисел з різними  цифрами можна скласти з набору

« 1; 2; 3; 4; 5»?

Розв’язання

.

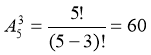Відповідь: 60 чисел.

3. На площині позначено  8 точок (жодні 3 не лежать на одній прямій). Скільки існує трикутників з вершинами в цих точках?

Розв’язання

.

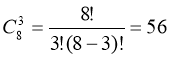Відповідь: 56 трикутників.

4. Скількома способами з 30 учнів класу можна обрати старосту, фізорга і редактора стінгазети?

Розв’язання

     =30∙29∙28=24360 способів.

Відповідь: 24360 способів.

5. Учню треба скласти 4 екзамени за 8 днів. Скількома способами можна це зробити за умови, що в один день не можна складати більше одного екзамену?

Розв’язання

=8∙7∙6∙5=1680 способів.

Відповідь:  1680 способів.

6. Скількома способами можна вибрати 3 фарби з 5 різних фарб?

Розв’язання

==10 способів.

Відповідь: 10 способів.

7. Обчислити .

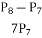Розв’язання

=1.

Відповідь: 1.

8. Скільки парних трицифрових чисел (усі цифри різні) можна записати, використовуючи цифри: «3; 4; 5; 7; 9»?

Розв’язання

Трицифрові числа повинні закінчуватися  на 4:    •  •  4.   Залишилося 2 порожніх місця та 4 вільні цифри, маємо:

.

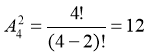Відповідь: 12 чисел.

9. Скільки існує трицифрових чисел, усі цифри якого непарні і різні?

Розв’язання

=5∙ 4 ∙3=60 чисел.

Відповідь: 60 чисел.

10.   У поштовому відділення зв’язку продається 10 видів листівок. Скількома способами можна купити 8 різних листівок?

Розв’язання

=45 способів.

Відповідь: 45 способів.

Завдання на 15 балів

1. На вершину гори ведуть 7 доріг. Скількома способами турист може піднятись на гору і спуститися з гори? Відповісти на те саме питання, якщо підняття і спуск відбуваються різними шляхами.

Розв’язання

 а) 7∙7=49 способів; б) 7∙6=42 способи.

Відповідь:49 способів, 42 способи.

2. В кабінеті банкіра є сейф з коштовностями, код до якого складається  з двох голосних букв і трьох цифр. Скільки комбінацій треба перебрати грабіжнику, щоб відкрити сейф і заволодіти коштовностями?

Розв’язання

.

Відповідь: 64800 комбінацій.      

3. У вазі стоїть 10 червоних і 5 рожевих пронумерованих гвоздик. Скількома способами можна вибрати  три квітки одного кольору?

Розв’язання

+=120+10=130.

Відповідь:   130 способів.

4. Розв’яжіть в натуральних числах рівняння 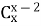=45.

Розв’язання

=45;  =45, =45;  за теоремою Вієта , Умову рівняння задовольняє – 10.

Відповідь: 10.

5. Скільки непарних семицифрових чисел можна записати за допомогою цифр 1,2,3,4,5,6,7 так, щоб у кожному числі цифри були різними?

Розв’язання

Число буде непарним, якщо  остання цифра числа також непарна. Вибір останньої цифри можна виконати 4 способами (1,3,5,7). Решту цифр можна обрати 6! способами. Всього способів 6!∙4=2880.

Відповідь: 2880 чисел.

6. Скільки трицифрових чисел можна записати за допомогою цифр 0,1,2,3,4,5,6?

Розв’язання

Спочатку розглянемо випадок, що цифри в утворених трицифрових числах не повторюються. У розряді можуть бути 6 із даних цифр (усі, крім 0), у розряді десятків також 6 – (усі, крім використаної в сотнях), у розряді одиниць – 5(усі, крім використаних двох), тому 6∙6∙5=180. Якщо цифри можуть повторюватись, то у розряді сотень може бути 6 із даних цифр (усі, крім 0), у розрядах десятків і одиниць по 7. Тому 6∙7∙7=294.

Відповідь: 180, якщо цифри не повторюються;  294, якщо цифри повторюються.

7. Є 6 різних квіток. Скільки існує способів скласти з них букет з 3 квіток або з 5 квіток?

Розв’язання

        Існує способів скласти букет з 3 квіток і способів скласти букет з 5 квіток.       Тоді існує способів скласти букет з 3 або з 5 квіток. Всього 26 способів.

Відповідь: 26 способів.

8. Розв’яжіть в натуральних числах рівняння .

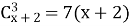Розв’язання

=7(х+2); (х+1)х=42; +х – 42=0; за теоремою Вієта  , Умову рівняння задовольняє – 6.

Відповідь: 6.

9. У шаховому гуртку 5 хлопці і 3 дівчини. Для зустрічі з гросмейстером прийшло 3 запрошення. Скількома способами можна розділити запрошення так, щоб на зустріч потрапила хоча б одна дівчина.

Розв’язання

«Хоча б одна дівчина» означає, що їх може бути одна, дві або три. Трьох осіб з усіх членів гуртка можна вибрати способами. Тільки трьох хлопців можна вибрати способами. В усіх інших варіантах будуть присутні дівчата. Отже, таких способів  -=56-10=46.

Відповідь: 46 способів.

7. Контроль знань,  умінь і навичок учнів

Поки журі підводить підсумки учні виконують самостійну роботу.

Відповіді до самостійної роботи.

Учні здають зошити на перевірку.

8. Підсумки уроку

Журі оголошує і нагороджує  команду-переможця. Найактивніші її учасники отримують оцінки.

9. Домашнє завдання

Учні отримують домашнє завдання і побажання успіху в подальшому вивченні теми: «Теорія ймовірності».

                   Скласти і розв’язати 5 комбінаторних  задач.