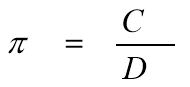Урок з теми "Коло. Довжина кола"

Урок № 62

Тема уроку: Коло. Довжина кола

Мета уроку:

Навчальна: сформувати більш строге геометричне уявлення про коло, його елементи та співвідношення між ними, дати зміст поняття «довжина» кола і виробити вміння знаходити довжину кола за відомим радіусом або діаметром та розв'язувати обернені задачі.

Розвиваюча: розвивати вміння висловлювати свою думку

Виховна: виховувати почуття дружнього відношення до товаришів, вміння висловлювати їх думку

Тип уроку: вивчення й первинне закріплення нових знань

Хід уроку: 1. ОРГАНІЗАЦІЙНИЙ МОМЕНТ

2. ПОВІДОМЛЕННЯ ТЕМИ ТА МЕТИ УРОКУ

3. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ

1.Серед фігур, зображених на рисунку, вкажіть ті, назви яких вам відо­мі. Назвіть ці фігури

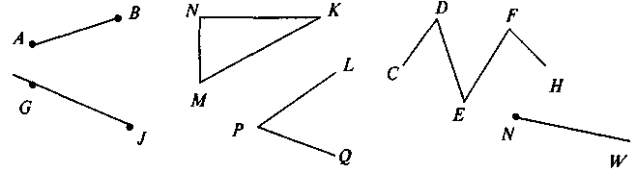
2.Точка М належить відрізку АВ, довжина якого 25 см. Знайдіть довжи­ни відрізків AM і ВМ, якщо: а) точка М — середина відрізка; б) AM більше за ВМ у 4 рази.             

4. ВИВЧЕННЯ  НОВОГО МАТЕРІАЛУ

1.Уявлення про коло

Математика — це не тільки наука про числа і дії з ними (цей розділ називається арифметикою); математика вивчає ще геометричні фігури і їх властивості (цей розділ математики називається геометрією). Серед багатьох інших гео­метричних фігур ми розглянемо дуже цікаву фігуру — коло.

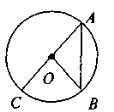
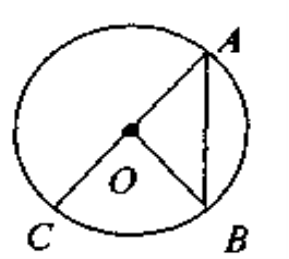
Як накреслити коло? Беремо циркуль і послідовно виконуємо дії: вибираємо точку, позначаємо її зазвичай літерою О; ставимо вістря цир­куля в т. О й проводимо іншим кінцем циркуля замкнену лінію — це і є коло. Отже, коло – це замкнена лінія, точки якої рівновіддалені від даної точки, яка називається центром кола.

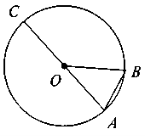Тепер називаємо елементи кола.

т .О — центр кола;

ОА, ОВ — радіуси кола - це відрізок, що сполучає центр кола з точкою, яка лежить на колі

 ОА = OB = R;

АС — діаметр –  це відрізок, що сполучає дві точки кола і проходить через його центр.

АС = D.

АВ— хорда – це відрізок, що сполучає дві точки кола

В будь-якому колі можна провести безліч радіусів, хорд, діаметрів.

2.Співвідношення між діаметром і радіусом кола

На рисунку бачимо: на АС лежить т. О, причому AO=OC = R , отже, О — середина АС, тому АО = CO = АС : 2, тобто R = D : 2, звідки D = 2R.

3.Довжина кола, число π

Mи з'ясували, що коло — це лінія, яку рисує кінець циркуля, вістря якого знаходиться у т. О — центрі кола. Але ж кожна лінія має довжину. Як же знайти довжину кола? Чи можна її виміряти (обчислити)?

Проведемо такий експеримент. Поставте круглу склянку на аркуш паперу та обведіть її олівцем. Отримаємо коло. Візьміть нитку та об­ведіть нею склянку. Випряміть нитку та виміряйте її довжину. Виміряй­те діаметр кола. Знайдіть відношення довжини кола до його діаметра. Давайте зробимо висновок: довжина кола приблизно у 3 рази більша за його діаметр. Відношення довжини кола до довжини його діаметра дорівнює тому самому числу для всіх кіл. Це число позначають грецькою буквою π.  Позначення літерою π не випадкове, бо це перша літера в грецькому слові περιφερια («периферія») — коло, круг.  Число π  - нескінченний десятковий дріб. π = 3, 14159265358979…Перші шість значущих цифр числа π  можна  запам’ятати за допомогою (рос. мо­вою):

При обчисленнях округлюють: π = 3, 14

Отже, C = πD або C = 2πR, де С -  довжина кола.

Запишіть опорний конспект:

5.ФОРМУВАННЯ ВМІНЬ

Усі задачі, які розв'язуємо на уроці можна умовно поділити на 2 групи:

а) задачі на застосування формули D = 2R;

б) задачі на застосування формули C = πD.

1. Виконання усних вправ: № 679, 681

2. Виконання  письмових вправ: № 685, 686

Задачі на застосування формули D = 2R.
Знайдіть радіус кола, якщо:

а) його діаметр 2 см; 2 м 3 см; 2,6 дм; 1,5 дм;

б) його діаметр більший за радіус на 5 дм; 3 м; 2,5 см.

Задачі на застосування формули C = πD = 2πR.

1) Знайдіть довжину кола, якщо:

а) діаметр 2,5 см; 24 см; 0,32 м; б) радіус 5 см; 4, 2 см; 0,8 дм.

2) Довжина кола дорівнює 33 м. Знайдіть діаметр кола ().

Це задача обернена (необхідно показати, що з формули C = πD можна виразити , а з формули С = 2πR ).

3) Довжина кола збільшилась з 157 см до 226,08 см. На скільки збільшився радіус кола?

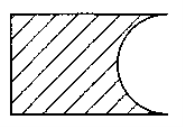
4) Із прямокутника вирізали півкруг (рис).

Зробіть необхідні вимірювання і знайдіть пе­риметр утвореної фігури.

6. ПІДСУМКИ УРОКУ

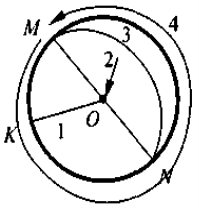«Німий» диктант»

Назвіть на малюнку об'єк­ти:

1 — радіус ОК;

2 — центр О;

3 — діаметр MN;

4 — коло.

5. π · MN - ? (С — довжина кола)

7. ДОМАШНЄ ЗАВДАННЯ

§16 ст. 116-117,  №687,

Задача 1. Знайдіть довжину кола:

а) якщо довжина діаметра 3 см; 0,6 дм

б) довжина радіуса 6 см; 1,2дм

Задача 2. Довжина кола дорівнює 2,2 м. Знайдіть діаметр кола ().