Урок з теми "Визначення прискорення вільного падіння".

Фізика, 10 клас.

Урок-залік з теми «Механічні коливання».

Спосіб проведення. Лабораторна робота: «Визначення прискорення вільного падіння».

Мета:   -закріпити та розвинути теоретичні та практичні знання та навички  учнів з теми «механічні коливання»;

             -поглибити знання з історії даного досвіду людства;

             -розвиток комунікативних навичок учнів під час роботи в команді;

             -контроль набутих знань та навичок на попередніх уроках.

Обладнання: Цифрова лабораторія, штативи, пружини, важки, кулі на нитці, учнівські лінійки та мірні стрічки. (див. фото 1 у додатку).

План уроку:

1. У відповідності за наявності цифрового обладнання, клас ділиться на команди. В моєму випадку є тільки набір для вчителя, отже, я ділю клас на три команди, які отримують відповідні завдання:

-команда № 1. Визначення прискорення вільного падіння за допомогою математичного маятника;

-команда № 2. Визначення прискорення вільного падіння за допомогою пружинного маятника;

-команда № 3 інформативного супроводу. Учні заздалегідь шукають в інтернеті інформацію про прискорення вільного падіння та історію його визначення.  Готують коротку доповідь із презентацією. Деякі найважливіші моменти, що освітили учні цієї команди, приведені у п. 2.

2. Прискорення вільного падіння g (зазвичай вимовляється як "ЖЕ") - прискорення, що надається тілу в вакуумі силою тяжіння, тобто геометричній сумою гравітаційного тяжіння планети (або іншого астрономічного тіла) і інерційних сил, викликаних її обертанням. Відповідно до другого закону Ньютона, прискорення вільного падіння чисельне дорівнює силі тяжіння, що діє на об'єкт одиничної маси. Г. Галілей довів, що прискорення вільного падіння не залежить від маси тіл і є сталою величиною. Також воно залежить від географічної широти місцезнаходження тіла, його відстані від центра планети, часу доби та інших факторів. Згідно з рішенням третьої Генеральної конференції мір та ваг у 1901 році, було прийняте стандартне значення прискорення вільного падіння g = 9,80665 м/с² . Реальне прискорення вільного падіння на поверхні Землі знаходиться у діапазоні від 9,780 м/с² на екваторі до 9,832 м/с² на полюсах. Ця різниця значень зумовлена обертанням Землі навколо своєї осі.

3. Математичний маятник. (Команда №1)

Математичним маятником називають матеріальну точку, підвішену на невагомій і нерозтяжній нитці. Це ідеальна коливальна система. На тіло діятимуть (якщо знехтувати силами тертя і опору повітря) сила тяжіння m·g, сила натягу нитки , рівнодійна яких буде надавати матеріальній точці прискорення. Це прискорення буде напрямлене в бік положення рівноваги. При малому відхилені математичний маятник здійснює гармонічні коливання. Якщо відхилення велике, то коливання маятника періодичні, але не гармонічні. У 1673 році Х. Гюйгенс опубликовав класичну працю з механіки «Маятниковий годинник» де отримав формулу періоду коливань математичного маятника:

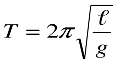
Із формули періоду коливань отримуємо вираз для розрахунку прискорення вільного падіння:

g=4·π² ·l/T²,

де l-довжина маятника, T–період коливань. Таким чином, для визначення значення прискорення вільного падіння треба визначити довжину підвісу l, та період коливань T.

Хід роботи:

1. Підвісити математичний маятник до штативу таким чином, щоб кулька вільно проходила у просвіт датчика «фотоворота» (див. фото 2 у додатку).

2. Виміряти довжину підвісу  l.

3. Відхилити маятник на невеликий кут, та відпусти.

4. Запустити програму, та визначити період коливань Т (див. Скріншот 1,2).

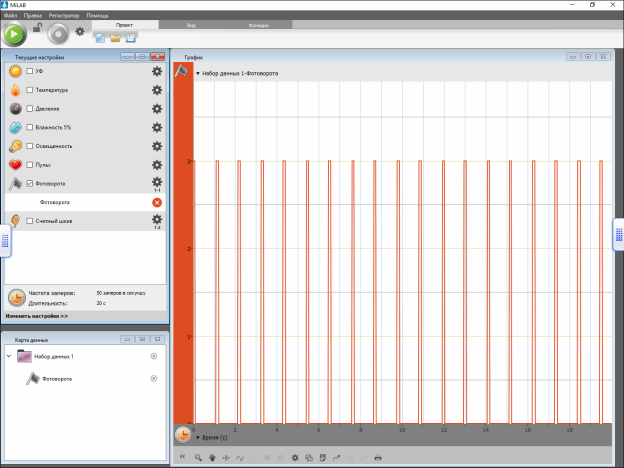
Скріншот 1. Розгортка у часі коливань математичного маятника зроблена за допомогою цифрового датчика «фотоворота».

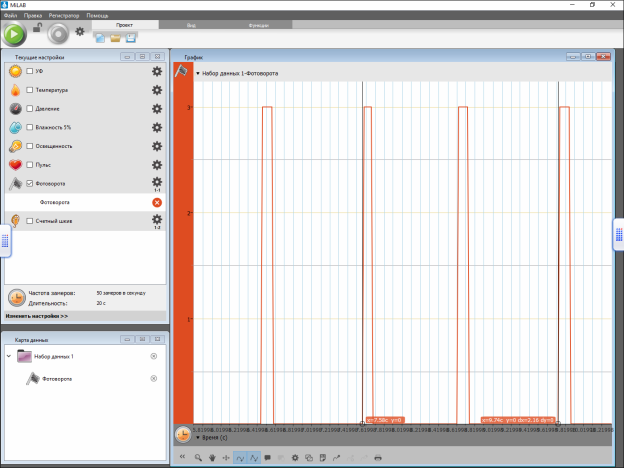
Скріншот 2. За допомогою інструментів керування програмою виділяємо ділянку, що відповідає одному періоду коливання математичного маятника.

Данні, що отримали учні під час виконання роботи:

довжина підвісу l=1,137 м; період коливань Т=2,16 с (див. Скріншот 2). Результат g=9,62084 м/с².

Різниця між дійсним значенням вимірювальної величини і одержаним нами результатом при досліді називається абсолютною похибкою ∆g=|g - g_д|, отже

∆g=0,18581 м/с².

 Відносною похибкою вимірювань називається відношення абсолютної похибки до значення вимірювальної величини:

ε=1,895%.

4. Пружинний маятник. (Команда № 2)

Пружинний маятник являє собою тягарець, що коливаеться на пружині. На тіло діятимуть (якщо знехтувати силами тертя і опору повітря) сила тяжіння m·g, сила пружності , рівнодійна яких буде надавати важку прискорення. Формула періоду коливань пружинного маятника:

Із цієї формули можна отримати вираз для знаходження коефіцієнта жорсткості пружини

k=4·π^2·m/T² (1)

З іншого боку, якщо тягарець знаходиться у рівновазі, тоді згідно із першим законом Ньютона маємо

g=k·Δx/m (2).

Підставивши (2) в (1), маємо остаточну формулу для розрахунку:

g=4·π²·Δx/T²

Таким чином, для визначення значення прискорення вільного падіння треба визначити видовження пружини Δx та період коливань T.

Хід роботи:

1. Підвісити пружину з важком до датчика сили, що прикріплений до штатива (див. фото 3,4 у додатку).
2. Визначити видовження пружини Δx.
3. Відтягнути пружину на невеличку відстань від положення рівноваги, та відпустити.
4. Запустити програму, визначити період коливань Т (див. Скріншот 3,4).

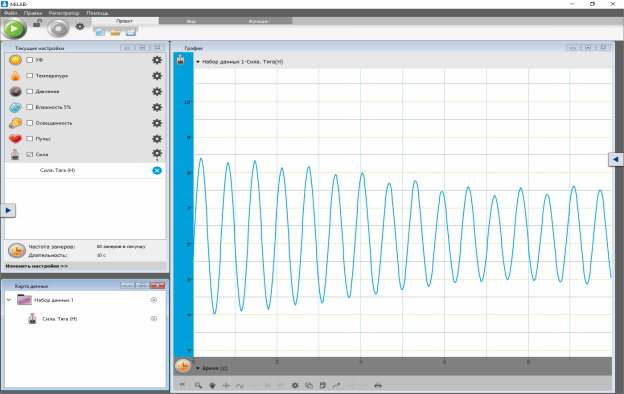
Скріншот 3. Розгортка у часі коливань пружинного маятника, зроблена за допомогою цифрового датчика сили.

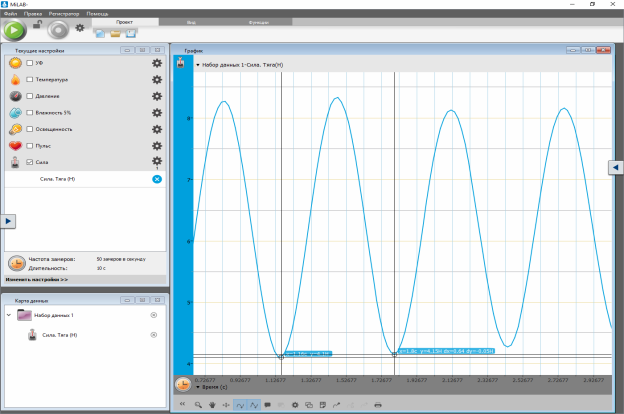
Скріншот 4. За допомогою інструментів керування програмою обираємо ділянку, на якій визначаємо період коливань пружинного маятника.

Данні, що отримали учні під час виконання роботи:

Видовження пружини Δx=9,91 см; період коливань Т=0,64с (див. Скріншот 4).

Результат g=9,55154 м/с²,

абсолютна похибка ∆g=0,25511 м/с²,

відносна похибка ε=2,6%.

Додаткові запитання для обговорення:

1. Що в цих методах є головним джерелом похибок?
2. Який маятник допомагає визначити прискорення вільного падіння з більшою точністю?
3. Який маятник допоможе визначити масу тіла у невагомості?
4. Чому у пружинного маятника швидко змінюється амплітуда коливань? (Скрин 3). (Якщо не вистачає часу уроку, це питання обов’язково треба обговорити пізніше. Я вважаю, що швидка зміна амплітуди обумовлена ні тим, що коливання швидко затухають, а тим, що маятник починає коливатися ще й у горизонтальній площині. Отже, ми спостерігаємо накладання коливань, в певному сенсі, амплітудну модуляцію вертикальних коливань горизонтальними. Ці знання знадобляться під час вивчення теми «Основи радіозв’язку»).

Висновоки:

-визначення прискорення вільного падіння в данній місцевості за допомогою  цифрового обладнання стає таким простим, що дозволяє досягти одразу декілька цілей, а саме: визначати цю величину одночасно різними способами, що дає можливість аналізу, контроль знань та умінь учнів, запровадження на уроці групових методів;

-значною перевагою виконання цієї роботи за допомогою цифрового комплексу є те, що не потрібно рахувати певну кількість коливань маятника за певний час, для того щоб розрахувати період коливань. Це дуже економить час, та зменшує похибки;

-також, цей метод дає можливість показати розгорнуту у часі динаміку процесу, що, в свою чергу допомагає розвитку головної, на мій погляд, якості людського інтелекту: аналізу.

Додаток.

Фото 1.

Фото 2.

Фото 3.

Фото 4.

Ресурси, що використовувалися під час підготовки до уроку:

1. https://uk.wikipedia.org/wiki/%D0%9F%D1%80%D0%B8%D1%81%D0%BA%D0%BE%D1%80%D0%B5%D0%BD%D0%BD%D1%8F_%D0%B2%D1%96%D0%BB%D1%8C%D0%BD%D0%BE%D0%B3%D0%BE_%D0%BF%D0%B0%D0%B4%D1%96%D0%BD%D0%BD%D1%8F
2. https://uk.wikipedia.org/wiki/%D0%94%D0%BE%D1%81%D0%BB%D1%96%D0%B4_%D0%93%D0%B0%D0%BB%D1%96%D0%BB%D0%B5%D1%8F_%D0%B7_%D0%BF%D0%B0%D0%B4%D1%96%D0%BD%D0%BD%D1%8F%D0%BC_%D1%82%D1%96%D0%BB
3. https://naurok.com.ua/library/vilne-padinna-2952.html
4. https://studopedia.info/ukr/1-2174.html

План-конспект складений учителем Бердянської гімназії № 3 «Сузір’я» Шадріним Володимиром Валерійовичем.     shadrinphis@gmail.com