Урок за темою "Теорема Піфагора"

8 клас                    

  Геометрія                                                                                  8 клас

Теорема Піфагора

 Мета уроку. Формувати вміння та навички розв’язування задач на застосування теореми Піфагора. Ознайомлення учнів з історичним матеріалом. Розвивати інтерес до предмета, логічне мислення. Сприяти формуванню вмінь та навичок застосовувати вивчені правила та властивості до розв’язування вправ, аналізувати,узагальнювати та структурувати здобуті знання, навички;виховувати уважність, наполегливість,активність на уроці. Виховувати точність і охайність.

Тип уроку. Урок формування вмінь та навичок.

Девіз уроку. Світ, що нас оточує – це світ геометрії. Тож давайте 

                        його пізнавати!

Хід уроку.

І. Перевірка домашнього завдання та актуалізація опорних знань учнів.

                         а² =                                                х                17

                         в² =                  12            х                        

   в              с    с² =                             9                               15

                                                            9

             а

                                                                                         х    

                                              х

                                                                                               11

ІІ. Мотивація навчальної діяльності учнів, повідомлення теми, мети і задач уроку.

Знання з математики - це ланцюжок, кожна ланка якого - знання з певної теми. І якщо не засвоїти якусь тему, то ланцюжок розірветься. Однією з таких дуже важливих ланок є тема «Теорема Піфагора».

Теорема Піфагора – основа евклідової геометрії. Завдяки їй можна довести  більшість теорем геометрії. Тому її треба добре засвоїти. Сьогодні у нас урок, на якому ми будемо розв’язувати задачі на застосування теореми Піфагора.

ІІІ. Усний журнал.

У світі відомо понад 100 різних доведень теореми Піфагора.

Піфагор, чиїм іменем названо теорему жив у VI ст. до н. е. Тоді математика тільки складалася у греків в теоретичну науку і Піфагор мав на неї великий вплив.

 Піфагор багато подорожував, його ім’я було оточене масою легенд, тому тепер важко визначити, що зробив Піфагор сам, а що запозичив у інших. У всякому разі, залежність між сторонами прямокутного трикутника була відома ще за 1000 років до Піфагора в Древньому Вавилоні та Єгипті. Піфагору, очевидно, належить заслуга доведення цієї теореми і широкого застосування її при розв’язуванні задач.

Теорема Піфагора  чудова тим, що сама по собі вона зовсім не очевидна. Скільки  не дивися на прямокутний трикутник, ніяк не побачиш, що між його сторонами є таке просте співвідношення:

с² = а² + в². 

Але це співвідношення стає очевидним, якщо вдало побудувати малюнок. В цьому і є найкращий геометричний стиль: за допомогою дотепної побудови зробити неочевидне очевидним. В математичних трактатах Древньої Індії, доводячи теорему, часто наводили тільки малюнок, супроводжуючи його лише одним словом «Дивись!»

 Давайте подивимось і ми!

В книзі І „Начал” Евклід цю теорему формулював так: „Твердження 47. В прямокутних трикутниках  квадрат на стороні, що стягує прямий кут, дорівнює разом узятим квадратам на сторонах, що утворюють прямий кут”.

Легенди розповідають, що коли Піфагор довів свою теорему, він віддячив богам, принісши їм у жертву 100 биків.

IV. Формування вмінь та навичок учнів розв’язування задач.

Робота з підручником.

1.Сторони прямокутника відносяться як 3:4, а його діагональ дорівнює 50 см. Знайти периметр прямокутника.

2. Чи можна застосовувати теорему Піфагора?

                                                           3                            5                                                     

                                                                           х   

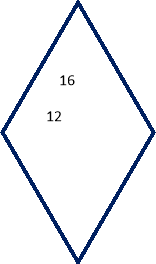
3. Від пристані одночасно відпливли два човна: один – на південь, зі швидкістю 16 морських миль в час, а другий – на захід зі швидкістю 12 миль. Яка відстань буде між човнами через 2,5 годин?

4. Додатково.

      0,5         1                                                            1

                                                                        х

          х             1                                                                     1

                                                                         1

V.  Самостійна робота (диференційовані завдання).  

Варіант А1.

1. Катети прямокутного трикутника дорівнюють 6 см і 8 см. Знайти довжину гіпотенузи.

2. Бічна сторона рівнобедреного трикутника  дорівнює 5 см, а висота, проведена до основи, - 4 см. Знайти периметр трикутника.

Варіант Б1.

1. Діагональ прямокутника дорівнює 13 см, а одна з його сторін – 12 см. Знайти периметр прямокутника.

2. Знайти периметр прямокутної трапеції, основи якої дорівнюють 2 см і 8 см,а більша бічна сторона – 10 см.

Варіант В1.

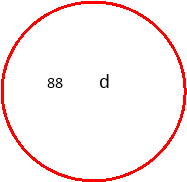
1. У колі радіуса 13 см проведено хорду на відстані    5 см від центра кола. Знайти довжину хорди.

2. В прямокутній трапеції більша діагональ дорівнює 15 см, а бічні сторони – 12 см і   13 см. Знайти середню лінію трапеції. 

Варіант А2.

1. Гіпотенуза прямокутного трикутника дорівнює 15 см, а один з його катетів – 12 см. Знайти довжину другого катета.

2. Основа рівнобедреного трикутника дорівнює 8 см,

 а висота, проведена до основи, - 3 см. Знайти периметр трикутника.

Варіант Б2.

1. Периметр прямокутника дорівнює 34 см, а одна з його сторін дорівнює 5 см. Знайти  діагональ прямокутника.

2. Знайти периметр рівнобічної трапеції, основи якої дорівнюють 3 см і 9 см, а висота – 4 см.

 Варіант В2.

1. У колі радіуса 15 см проведено хорду довжиною   18 см. Знайти відстань від центра кола до хорди.

2. В прямокутній трапеції менша діагональ дорівнює     13 см, а бічні сторони – 12 см і   20 см. Знайти середню лінію трапеції. 

VІ. Підсумки уроку і домашнє завдання.

.