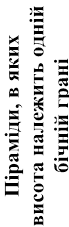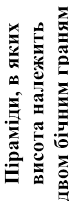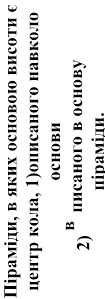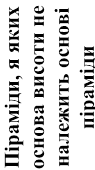Види піраміди за особливостями розміщення її висоти

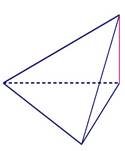
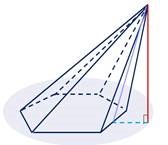
         Якщо одна із гране висота піраміди лежить із вершини піраміди до

й піраміди перпендикуляр

 у площині цієї грані і є пер прямої перетину площин ці

на до площини основи, то пендикуляром, проведеним єї грані й площини основ.

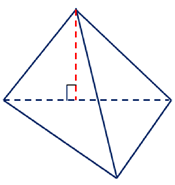
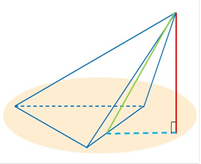
       Якщо дві бічні гран пряма їх перетину міст

і піраміди перпендикулярні ить висоту піраміди

 до площини основи, то

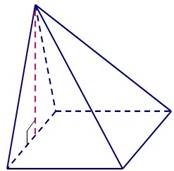
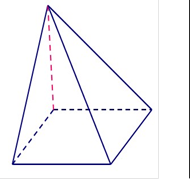
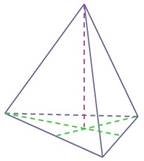
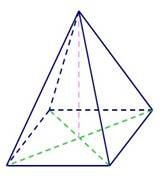
1) Якщо всі бічні ребра основи піраміди, або ут висоти піраміди є центр 2) Якщо всі двогранні к граней, проведені з вер проведені з вершини пі або висота піраміди утв

піраміди рівні, або однаков

ворюють однакові кути з ви  кола, описаного навколо о

ути при основі піраміди рів

шини піраміди, рівні, або вс раміди, утворюють однаков орює із площинами всіх біч

о нахилені до площини сотою піраміди, то основою

снови піраміди. ні, або всі висоти бічних

і висоти бічних граней,

і кути з висотою піраміди, них ребер однакові кути, то

основою висоти пірамід

и є центр кола, вписаного в

 основу піраміди.

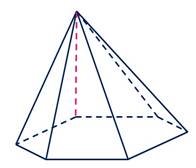
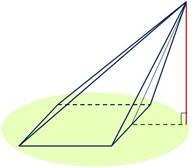
      Якщо ортогональна проекція вершини піраміди на її основу лежить поза основовою піраміди, то висотою піраміди буде відстань від вершини піраміди до площини, в якій лежить основа піраміди.