Відкртие заняття з математики на тему "Тригонометричні рівняння та способи їх розв'язування"

ВІДКРИТЕ ЗАНЯТТЯ З МАТЕМАТИКИ НА ТЕМУ «ТРИГОНОМЕТРИЧНІ РІВНЯННЯ. СПОСОБИ ЇХ РОЗВ’ЯЗУВАННЯ»

 

План відкритого заняття з математики на тему: «Тригонометричні рівняння. Способи їх розвязування»

 

Вид заняття:      Інформаційна лекція. Повідомлення і засвоєння нових знань.

Дисципліна:       «Математика»

Група:                  Г-11

Тема заняття:    Тригонометричні рівняння. Способи їх розв’язування.

Мета заняття

 навчальна:     Навчити студентів класифікувати різні типи         

                          тригонометричних рівнянь, а потім їх розв’язувати.

розвиваюча:   Розвивати логічне і нестандартне мислення студентів, пам'ять,     

                    математичну культуру мови і запису, вміння аналізувати і

   узагальнювати факти, робити висновки.

 виховна:         Виховувати у студентів почуття власної гідності, вміння  

                      правильно  і чітко формулювати свою думку, сприяти   

                          виявленню і розвитку розвитку математичних здібностей 

                          студентів.

Мета відкритого заняття:

Показати методику проведення лекційного заняття з елементами  бесіди, демонстрації, дослідження, з використанням електронних засобів навчання.

Матеріально-технічне забезпечення заняття: 

тригонометричні таблиці, стенди з ілюстративним матеріалом, мультимедійний проектор

Навчальне місце (аудиторія чи лабораторія):  аудиторія №307

 

Література (основна):

1. М.І.Шкіль, З.І.Слєпкань «Алгебра і початки аналізу 10 клас», Київ,

«Зодіак - ЕКО», 2002, розділ 2, §13.

2. Є.П.Нелін «Алгебра і початки аналізу 10 клас», Харків, вид. «Світ дитинства», 2005 р, розділ 2, §15.

3. В.Кравчук «Алгебра і початки аналізу 10 клас», Тернопіль, вид. «Підручники і посібники», 2006 р, розділ ІІІ, §15.

 

Література (додаткова):

1. А.Г.Мерзляк «Алгебра і початки аналізу», Харків, вид. «Гімназія», 2010, §5, п.51, п.52, п.53.

2. Я.Ф.Гап’юк, Я.Т.Гринчишин «Випускні екзамени. Завдання і розв’язки», Тернопіль, 1995 р.

 

 

 

 

 

 

Структура і хід заняття

1. Організаційна частина                                                                                                 Привітання, перевірка наявності і підготовки студентів до пари.             

 

2. Актуалізація опорних знань студентів і мотивація навчальної діяльності з оцінюванням відповідей                                                                                                             

 

        Запитання до студентів, які відповідають біля дошки

1.Тригонометричні функції довільного аргументу.

2. Властивості і графіки тригонометричних функцій.

3. Розв’язування найпростіших тригонометричних рівнянь.

 

Запитання до студентів на місцях

1. Тригонометричні функції кутів трикутника.

          2. Означення синуса і косинуса на одиничному колі.

3. Тригонометричні тотожності, які пов’язують один і той же аргумент.

4. Означення обернених тригонометричних функцій.

 

3. Повідомлення теми, змісту і послідовності вивчення нового матеріалу          

 

Тема заняття: Тригонометричні рівняння і способи їх розв’язування    

 

План заняття

 

1. Орієнтир для розв’язування тригонометричних рівнянь, які відрізняються від найпростіших

При пошуку плану розв’язування більш складних тригонометричних рівнянь   можна скористатися таким орієнтиром:

1. Пробуємо звести всі тригонометричні функції до одного аргументу.

 2. Якщо вдалося це зробити, то пробуємо всі тригонометричні вирази звести до однієї функції. 

3. Якщо до одного аргументу вдалося звести, а до однієї функції – ні, то спробуємо звести рівняння до однорідного.

4. В інших випадках переносимо всі члени рівняння в один бік і пробуємо одержати добуток або використовуємо спеціальні прийоми розв’язування.

 

2. Розв’язування тригонометричних рівнянь методом заміни змінної.

 При розв’язуванні тригонометричних рівнянь цим методом потрібно звести всі тригонометричні вирази до однієї тригонометричної функції. При цьому використовуються формули: ;

 

 

 

 

 

 

 

Приклад

                                      

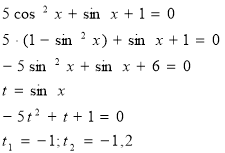
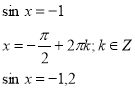
Рівняння немає розв’язку.

           

3. Розв’язування тригонометричних рівнянь способом розкладання на множники.

При розв’язуванні рівнянь цим способом потрібно всі члени рівняння перенести в один бік і попробувати одержати добуток, що дорівнює нулю.

Наведемо приклад:

         

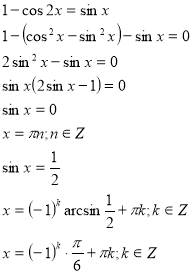
4. Розв’язування однорідних тригонометричних рівнянь.

Якщо всі члени рівняння мають однаковий сумарний степінь, то дане рівняння називається однорідним. Розв’язується однорідне рівняння діленням на найвищий степінь однієї із змінних.

Наведемо приклад:

 

Поділимо ліву і праву частину рівняння на

 

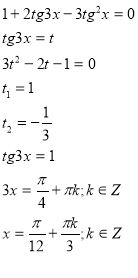
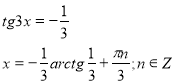
5. Розв’язування тригонометричних рівнянь способом введення допоміжного кута.

Загальний вигляд таких рівнянь:  . Ділимо ліву і праву частину даного рівняння на вираз виду . Отримуємо

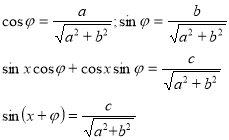
Отримали найпростіше тригонометричне рівняння відносно синуса. Наведемо приклад розв’язування таких рівнянь:

 

 

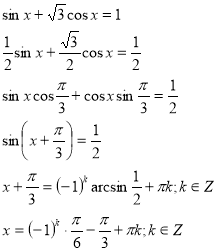
6. Дробо - раціональні рівняння відносно тригонометричних функцій.

При розв’язуванні таких рівнянь потрібно виконувати відбір коренів. Найчастіше це робиться так: знаходять найменший спільний період усіх тригонометричних функцій, що входять у запис рівняння; потім на цьому періоді відбирають корені (відкидають сторонні), а ті, що залишилися, періодично продовжують.

Наведемо приклад:

 

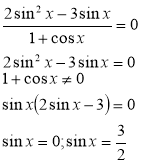
Відкидаємо непарні корені виду

Відповідь:

4. Узагальнення і систематизація знань 

 Узагальнення нового матеріалу, шляхом перегляду навчального відеофільму на      

тему « Способи розв’язування тригонометричних рівнянь». Див. додаток 7.                                                                    

5. Підсумки роботи студентів  

 Підведення підсумків заняття. Аналіз загальної активності студентів.

6. Домашнє завдання 

1. М.І.Шкіль, З.І.Слєпкань «Алгебра і початки аналізу 10-11 клас», Київ, «Зодіак-  ЕКО»,1996,  розділ 2, §3, №1- №6 .

 2. Є.П.Нелін «Алгебра і початки аналізу 10 клас», Харків, вид. «Світ дитинства», 2005 р, розділ 2, §15.

                                                        Викладач   Цівина Л.М.