Відпрацювання практичних умінь і навичок на уроках математики 6 клас

Си Тип уроку: відпрацювання практичних умінь інавичок.

Обладнання: проектор, ноутбук, роздатковий матеріал.

Хід уроку

І. Організаційний момент.

1) Перевірка домашнього завдання.

учні порівнюють свої відповіді та заздалегідь підготовлені записи відповідей на дошці

2) Гра «Четверте зайве».

потрібно встановити, яке слово або число зайве в заданому наборі

Математика, фізика, торгівля, економіка.

1000; лікоть; 0,3; вісім.

Градус, транспортир, метр, миля.

.

ІІ. Актуалізація знань.

1. Цікаві повідомлення про десяткові дроби.

повідомлення учнями та вчителем історичних та цікавих фактів про десяткові дроби готувалися вдома, використовуючи підручник з математики, книги з шкільної бібліотеки, мережу Інтернет та інші джерела інформації (наводимо лише деякі з них)

Учень 1. У підручнику [47, с. 262-263] сказано, що десяткові дроби пов’язані з десятковою системою числення. Проте їхня поява має більш давню історію і пов’язана з ім’ям видатного математика й астронома ал-Каші (повне ім’я – Джемшид ібн-Масуд ал-Каші). У праці «Ключ до арифметики» (ХV ст.) він уперше сформулював правила дій з десятковими дробами, навів приклади.

Але нічого не знаючи про відкриття ал-Каші, удруге «відкрив» десяткові дроби приблизно через 150 років фламандський математик та інженер Сімон Стевін. У праці «Децималь» (1585 р.) С. Стевін виклав теорію десяткових дробів. Він усіляко пропагував їх, підкреслюючи зручність десяткових дробів для практичних обчислень.

Учень 2. Відокремлювати цілу частину десяткового  дробу від дробової ал-Каші і С. Стевін пропонували по-різному. Так, ал-Каші цілу й дробову частини писав різними чорнилами або ставив між ними вертикальну риску. С. Стевін відокремлював частини десяткових дробів нулем у кружечку. Прийняту у наш час кому запропонував у 1592 році відомий німецький астроном Йохан Кеплер (1571 – 1630).

Нині в деяких країнах, наприклад у США, замість коми використовують крапку. У зв’язку з стрімким розвитком програмування використання крапки стає все популярнішим. Пригадайте, де ми використовуємо крапку під час запису десяткових дробів!

на слайді учні показують портрети згаданих науковців (рис.12)

Рис. 12. Портрети науковців.

Учень 3. Щоб не повторювати інформацію з підручника, здійснювався пошук цікавої інформації у мережі Інтернет. Зокрема, використавши джерело [10], хочу ознайомити клас із стародавніми мірами довжини, які були пов’язані з десятковими дробами (інформаціє подається на слайді презентації, рис. 13).

Рис. 13. Стародавні міри довжини.

Учитель. Чи задумувалися ви про те, які величини можуть позначати десяткові дроби? Наприклад (використано з [20]), дріб 0,001 – це на перший погляд невелике число (0,001 секунди – для нас у повсякденному житті це дуже мало). Але потяг зі швидкістю 72 км/год за цей час проїде 20 см; звук у повітрі пройде 33 см, а куля пролетить 70 см; Земна куля за це й же час проходить шлях по своїй орбіті навколо Сонця завдовжки 30 м; навіть комар встигає змахнути крилами вгору і вниз.

Дріб 0,000001 ще менший. Але для сучасного фізика-дослідника 0,000001 секунди – це зовсім немалий проміжок часу. Так, промінь світла за цей час пробігає 300 м.

Міліметр – це 0,001 м, що вдвічі менше від товщини сірника, однак для вимірювання хімічних процесів і реакцій це число є достатньо великим. Тут використовують мікрон – це 0,001 мм. Мікрон в 1000 раз менший від міліметра. Так звані червоні кров’яні тільця, яких у краплині крові близько 10 000 000, мають довжину 7 мк і товщину 2 мк. Усе в природі відносне і навіть числа.

2. Математичний диктант.

вчитель швидко зачитує речення (без повторень), а учні повинні записати в зошит лише пропущене в реченні слово

1. Результатом дії додавання є …
2. Результатом дії множення є …
3. Суму кількох однакових доданків можна замінити дією… 
4. Якщо один із доданків зменшити на три, то сума … на три.
5. Якщо один із множників зменшити у k-разів, то добуток …
6. Якщо знаменником правильного дробу є кругле число, то такий дріб називається …
7. Ціла і дробова частини десяткового дробу відокремлюється …
8. Один міліметр – це … частина сантиметру.
9. Між дробами 0,1 і 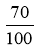можна поставити знак …
10. Якщо  ціла  частина  десяткового  дробу  дорівнює  нулю,  то  він  менший від …