Визначні математичні задачі. Позакласна робота

Визначні математичні задачі

 Всебічний розвиток будь-якої науки неможливий без глибокого аналізу її історії.

 До минулого ми звертаємось з різних причин. Відомий факт: без минулого, немає сучасного і тим більше немає майбутнього.

Математика має особливу привабливість. Задачі й теореми, доведені сотні й тисячі років тому, захоплюють нас своєю красою, витонченістю у доведеннях.

Математика, як наука, виникла з практичних потреб людини. Математичні поняття, ідеї в майбутньому були об’єднані у теорії.

Ми зупиняємося лише на одній старовинній задачі, яка дійшла до нас від цивілізацій Стародавнього Сходу – Єгипту.

Загадка жерців бога Ра.

Ти стоїш перед стіною, за нею криниця  Лотоса, як круг Сонця. Біля криниці покладено один камінь, одне долото, дві очеретини. Довжина однієї очеретини три міри, другої – дві міри. Очеретини перехрещуються на поверхні води криниці Лотоса, а ця поверхня на одну міру вища від дна. Хто повідомить число найдовшої прямої, яка міститься в ободі криниці Лотоса, той візьме обидві очеретини і буде жрецем бога Ра.

Криниця – це прямий круговий циліндр. Дві очеретини (3м і 2м) сперті на бічну поверхню циліндра і стоять на діаметрально протилежних точках основи. Проекції жердин на основу є діаметр криниці. Обчисли діаметр криниці.

У 1912 році під час розкопок у дельті Ніла вчені виявили залишки храму, на стінах якого збереглися письмена. Були тут і математичні задачі. Текст цієї задачі жреці бога Ра вирізьбили на стіні велетенської кімнати, побудованої з гранітних брил. Задача була одним з випробувань для бажаючих стати жрецями бога Ра. Це був важкий і небезпечний іспит, про що відверто застерігали жреці. Під її текстом вирізьблено попередження: « Знай: кожен може стати перед стіною. Хто розуміє справу рук жреців бога Ра, тому відкривається стіна для виходу. Але знай: коли ти ввійдеш, ти будеш замурований. Вийдеш з очеретинами жреців бога Ра і якщо ж голод переможе твоє тіло, не вийдеш жрецем бога Ра…

Крізь стіну криниці Лотоса пройшли багато, але мало хто став жрецем бога Ра. Думай. Цінуй своє життя. Так радять тобі жреці бога Ра».

Ця задача справді складна. Можна тільки дивуватися, як з нею справлялися стародавні єгиптяни. Очевидно, не одному з них вона коштувала життя.

Приступаємо і ми до розв’язання задачі жреців бога Ра.

Виконаємо осьовий переріз криниці.

За умовою AB=3м, CD=2м, OH=1м

Нехай AC=y, BC=x, тоді з ∆ ABC(C=90°) маємо перше рівняння x²+y²=9

∆AOH ∆ABC, тому = . Звідси AH = ;

HC = AC – AH = y - = ;

З ∆ACD (A = 90°) : ;

З ∆OHC (;

Оскільки = , то

1 + = ; або y² + = 4.

Розв’яжемо систему рівнянь:

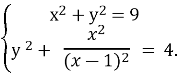
Віднімемо рівняння – x² = -5

Це рівняння зводиться до рівняння x⁴ – 2x³ – 5x² + 10x – 5 = 0.

Алгебраїчне рівняння 4-го степеня маэ вигляд

x⁴ + ax³ + bx² + cx + d = 0 (1)

За допомогою підстановки x = y - можна звести до рівняння

y⁴ + py² + qy + v = 0 (2)  в якому коефіцієнт при y³ дорівнює нулю.

 Виконаємо підстановку x = y + .

(y + )⁴ – 2(y + )³ – 5(y + )² + 10(y + ) – 5 = 0

( y² + y + )² – 2( y³ + y² + y + ) – 5( y² + y + ) + 10y = 0

y⁴ + y² + + 2y³ + y² + y – 2y³ – 3y²  - y  -  – 5y² – 5y - + 10y = 0

y⁴ – 6,5y² + 4y - , або

16y⁴ – 104y² + 64y – 23 = 0

Заміна : 2y = t,   тоді наше рівняння набуде вигляду

t⁴ – 26t² + 32t – 23 = 0

Рівняння (2) потім запишемо у вигляді

(y² + + α)² – ( 2αy² – qy + ( α² + pα – v + )) = 0

Скористаємося цим. Одержимо:

(t² – 13 + α)² – (2αt² – 32t + α² - 26α + 192) = 0    (3)

Щоб утворити різницю квадратів у лівій частині рівняння необхідно щоб многочлен у 2-х дужках можна було записати у вигляді квадрата. Це можливо тоді, коли дискримінант квадратного тричлена дорівнює нулю.

 

, тому

 

При розв’язанні повних кубічних рівнянь роблять підстановку

    (4)

Після цього рівняння набуває вигляду  (5)

Наша підстановка

 

  або 27k³ - 900k + 6320=0

Заміна: 3k=z, тоді одержимо: z³ – 300z + 6320=0     (6)

Корені зведеного кубічного рівняння знайдемо по формулі

X=U+V де

,      

Ці формули називають формулами Кардано (італійського математика, філософа і лікаря, 24.9.1501 - 21.2.1576), які він запозичив у італійського математика (Нікколо Тарталья ) близько 1500-13.12.1557)

Всі три корені виражаються формулами x₁=U+V,    x₂=UE+VE²,   x₃=UE³+VE.

Якщо рівняння має комплексні корені, то вони виражаються справжніми числами х₂ і х₃.

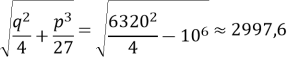
Z=U+V/

Оскільки 3K=Z, то  ; ;

Але , .

Повертаємось до рівняння (3).

(t² – 13 + 0,738)² – (1,476t² – 32t + 173,357) = 0

(t² – 12,262)²-( 1,215t – 13,1665)² =0

У першому рівнянні корені комплексні. Друге рівняння має корені

нас не задовольняє і .

Далі 2y=t, .

Нарешті .

Тобто ВС

З ∆AВC (С = 90°): АС=.

Нарешті діаметр криниці.

Розв’яжемо кубічне рівняння (6) іншим способом. Кубічне рівняння виду розв’яжемо, виконавши підстановку

, отже

Виконаємо підстановку

, тоді

     z =a₁+b₁=a₂+b₂.

Тому z=-23,7448

Потім розв’язання йде в руслі попередніх перетворень.

Задачу жерців бога Ра розв’яжемо інакше.

 

Зобразимо основний переріз криниці.

Нехай АВ=3 м, CD=2 м, ОНАС, ОН=1 м.

Нехай ВС=х, АD=у.

З ∆AВC (С = 90°): , а

З ∆ADC (A = 90°):

Віднімемо ці рівності  у² -  (1)

∆AОD∆ВОC, тому у:х=ОА:ОВ  (2).

Сторони перетнули паралельними прямими ОН і ВС, тому ОА:ОВ=АН:НС. В рівності (2) виконаємо заміну: у:х=АН:НС (3)

∆AВС∆АОН,  тому х:ОН=АС:АН; ОН=1 м,

тому . В останню рівність підставимо результат рівності (3). Одержимо:

або ху=х+у  (4)

З рівнянь (1) і (4) одержимо систему рівнянь:

;  .

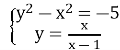Після нескладних перетворень одержимо рівняння

Виділимо квадрат двочлена

.

Ще  раз виділимо квадрат двочлена, ввівши параметр

;

;

      (1)

Щоб праву частину рівняння подати у вигляді квадрата треба,щ об дискримінант квадратного тричлена дорівнював нулю.

.

Щоб повне кубічне рівняння   звести до рівняння

виконаємо заміну ;

Маємо: ;

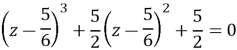
або   216z³ - 450z+790=0

Заміна 6z=t, тоді одержимо рівняння   (2)

Знову використаємо формули Кардано.

t=U+V де

,       ,  p=-75,   q=790

 

.

;

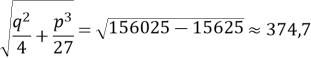
6z=t,

Значення підставимо у рівняння (1)

або

 

 

– не задовольняє умову

Тобто ВС.

З ∆AВC:

Діаметр криниці знайдено.

Оскільки кубічне рівняння ми звели до вигляду то розв’яжемо по іншому  рівняння (2) використавши підстановку a+b=х і .

a+b=t,  , ab=25

, тоді

;     ;    

t =a₁+b₁=a₂+b₂.

.

Повертаючись аналогічно через заміни назад приходимо до того, що діаметр криниці

Оскільки стародавні єгиптяни не вміли розв’язувати рівнянь 4-го степеня (строге доведення розв’язку рівняння 4-го степеня в радикалах зробив норвежський математик Нільс  Абель, 1824р.), тому задачу жерців бога Ра вони розв’язували так.

На підлозі кімнати вони креслили пряму КР.

Враховуючи, що АВ-СD=1м, проводимо на відстані 1 м від прямої КР пряму MN (MN||KP)

Потім опускали очеретини в криницю і позначали на них місце їх схрещення, рівень води. Потім очеретини клали на креслення так, щоб точка перетину О лежала на прямій MN і обертали їх, щоб мокрі краї очеретин А і С натрапили на пряму КР.

Після цього вимірювали наближено АС, використовуючи одну з очеретин.

Сьогодні відомо багато способів розв’язання рівнянь вище квадратичних. Вони дозволяють з високою точністю шукати корені.

Пригадаємо їх.

Це зокрема: Правило Декарта, спосіб дотичних (спосіб Ньютона), спосіб хорд (спосіб лінійної інтерполяції), спосіб для наближеного визначення найбільшого і найменшого по модулях величин кореня; метод ітерації, метод Чебишева.