Вписані чотирикутники

Тема: Вписані чотирикутники

Мета:

• Навчальна: сформулювати означення кола, описаного навколо чоти­рикутника та чотирикутника, вписаного у коло; засвоїти властивість та ознаку вписаного у коло чотирикутника; засвоїти наслідки з теорем про вписаний у коло чотирикутник;
• Розвиваюча: розвивати пам’ять, логічне мислення, самостійність, продовжувати формування математичної мови, вміння відтворювати зміст вивченого матеріалу, використовувати нові означення до розв’язування задач
• Виховна: виховувати наполегливість, естетичність у оформленні конспекту, вміння грамотно висловлювати свої думки, виховувати вміння об’єктивно оцінювати здібності

Тип уроку: засвоєння нових знань і навичок, формування вмінь

Хід уроку

1. Організаційний етап
2. Актуалізація опорних знань

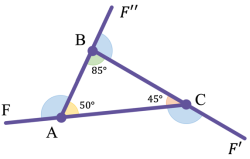Зовнішній кут трикутника

Якою є градусна міра ()

Якою є градусна міра

()

Якою є градусна міра ()

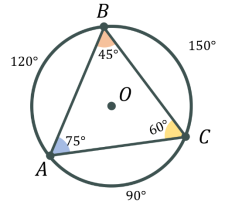
• Теорема про вписаний кут

• Якою буде градусна міра

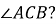
• Якою буде градусна міра

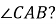
• Якою буде градусна міра

3. Вивчення нового матеріалу

• Проблемне питання

•      Якщо коло описане навколо трикутника, де будуть знаходитися всі його вершини?
•      Чи навколо будь якого трикутника можна описати коло?
•      Чи навколо кожного чотирикутника можна описати коло?

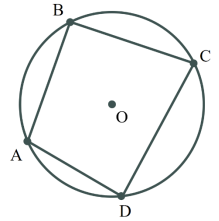• Вписані чотирикутники

•             Спробуйте самостійно сформулювати означення чотирикутника, вписаного в коло.

Чотирикутник називається вписаним у коло, якщо всі його вершини лежать на цьому колі.

•             Як тоді назвати таке коло?

Коло називається описаним навколо чотирикутника, якщо воно проходить через усі його вершини.

Теорема (властивість вписаного чотирикутника)

Сума протилежних кутів вписаного чотирикутника дорівнює .

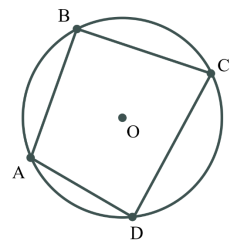*Доведення в презентації супроводжується анімацією

Дано:

– вписаний у коло чотирикутник

т. – центр кола

Довести:

Доведення:

За теоремою про вписані кути:

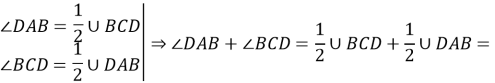
Виконайте аналогічне доведення для інших кутів.

Доведено.

Теорема (ознака вписаного чотирикутника)

Якщо сума протилежних кутів чотирикутника дорівнює , то навколо нього можна описати коло.

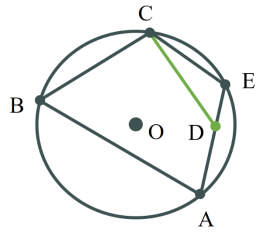*Доведення в презентації супроводжується анімацією

Дано:

– чотирикутник

Довести:

– можна вписати у коло

Доведення:

1.     Опишемо коло навколо 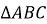. За умовою .
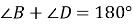2.     Методом від супротивного доведемо, що т. 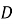може лежати тільки на колі.

Припустимо, що т. лежить усередині кола.

– точка перетину променя з колом.

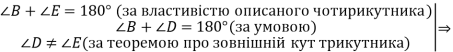отримали суперечність

Виконайте аналогічне доведення для інших кутів.

Отже, точка – лежить на колі, тобто навколо чотирикутника – можна описати коло.

Доведено.

•      Як інакше можна сформулювати ці дві теореми?

Чотирикутник вписаний в коло тоді й тільки тоді, коли сума двох його протилежних кутів дорівнює

Наслідок 1

Навколо будь-якого прямокутника можна описати коло.

Якщо паралелограм вписаний у коло, то він є прямокутником.

*Центр описаного навколо чотирикутника кола, є точкою перетину серединних перпендикулярів, проведених до його сторін

*Центр описаного навколо прямокутника кола

збігається з точкою перетину його діагоналей

Налідок 2

Навколо рівнобічної трапеції можна описати коло.

Якщо трапеція вписана в коло, то вона рівнобічна.

4. Закріплення нових знань та вмінь учнів

№ 1

Знайдіть невідомі кути:

а) Вписаного чотирикутника, якщо два його кути дорівнюють ;

б) Вписаної трапеції, якщо один з її кутів дорівнює ;

в) Вписаного чотирикутника, діагоналі якого точкою перетину діляться навпіл;

№ 2

Чотирикутник вписаний у коло, центр якого лежить на стороні Знайдіть кути чотирикутника, якщо

№ 3

У трикутнику висоти і перетинаються в точці . Доведіть, що точки лежать на одному колі

5. Підсумок уроку

• Який чотирикутник називається вписаним у коло?
• Сформулюйте властивість вписаного чотирикутника
• Сформулюйте ознаку вписаного чотирикутника
• Що можна сказати про паралелограм, навколо якого описано коло?
• Що можна сказати про трапецію, навколо якої описано коло?

6. Домашнє завдання