Курсова робота на тему Використання ІКТ при вивченні розділу «Тригонометричні рівняння й нерівності» шкільного курсу алгебри і початків аналізу
Курсова робота
Допомога при викладанні курсу Алгебра та початки аналізу
Тема “Нерівності" займає важливе місце в курсі алгебри. Вона багата за змістом, за способами та прийомами розв'язування, за можливостями її застосування при вивченні ряду інших тем шкільного курсу алгебри. Це пояснюється тим, що рівняння і нерівності широко використовуються в різних розділах математики, у вирішенні важливих прикладних задач.
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
НАЦІОНАЛЬНИЙ ПЕДАГОГІЧНИЙ УНІВЕРСИТЕТ
ІМЕНІ М. П. ДРАГОМАНОВА
Факультет перепідготовки та підвищення кваліфікації
Кафедра освіти дорослих
Курсова робота
з методики навчання математики
на тему
Використання ІКТ при вивченні розділу «Тригонометричні рівняння й нерівності» шкільного курсу алгебри і початків аналізу
Виконала
слухачка 61 мі групи
спеціальності «математика»
Овдієнко Ірина Володимирівна
Науковий керівник
кандидат фізико-математичних наук,
доцент Деканов С. Я.
Роботу захищено «__» ________ 2018 р.
з оцінкою _________________________
Комісія: ___________________________
___________________________________
___________________________________
Київ – 2018
План
Вступ
- Загальні питання вивчення тригонометричних рівнянь і нерівностей в курсі алгебри 10 класу.
- Короткий опис ІКТ, які можливо використати при вивченні даного розділу.
-
Методика викладання теми «Тригонометричні рівняння та нерівності» з використанням ІКТ.
- Використання презентацій Microsoft PowerPoint.
- Використання GRAN1.
- Використання DERIVE.
- Використання Mathcad.
- Контрольно-діагностичні системи TEST-W і MyTestХ.
Висновки
Вступ
Рівняння в шкільному курсі алгебри займають провідне місце. На їх вивчення відводиться часу більше, ніж на будь-яку іншу тему шкільного курсу математики. Сила теорії рівнянь в тому, що вона не тільки має теоретичне значення для пізнання природних законів, але і служить конкретним практичним цілям. Більшість задач, що стосуються просторових форм і кількісних відношень реального світу, зводиться до розв’язування різних видів рівнянь. Навчившись їх розв’язувати, люди знаходять відповіді на різні питання з науки і техніки (транспорт, сільське господарство, промисловість, зв’язок і т. д.). Також для формування вміння розв’язувати рівняння велике значення має самостійна робота учня при навчанні розв’язування рівнянь. При вивченні будь-якої теми рівняння можуть бути використані як ефективний засіб закріплення, поглиблення, повторення і розширення теоретичних знань, для розвитку творчої математичної діяльності учнів.
Тема “Нерівності” займає важливе місце в курсі алгебри. Вона багата за змістом, за способами та прийомами розв’язування, за можливостями її застосування при вивченні ряду інших тем шкільного курсу алгебри. Це пояснюється тим, що рівняння і нерівності широко використовуються в різних розділах математики, у вирішенні важливих прикладних задач.
1. Загальні питання вивчення тригонометричних рівнянь
і нерівностей в курсі алгебри 10 класу
Розділ «Тригонометричні рівняння, нерівності та їх системи» в курсі алгебри і початків аналізу 10 класу розрахований на 13 годин і складається з 5 тем:
- обернені тригонометричні функції;
- найпростіші тригонометричні рівняння;
- окремі способи розв’язування тригонометричних рівнянь;
- розв’язування систем тригонометричних рівнянь;
- найпростіші тригонометричні нерівності.
Кожна з тем розрахована на два уроки:
- урок-лекція (бесіда),
- урок-практикум.
На кожному уроці лекції-бесіди (крім першого) ⅓ частину уроку займає перевірка домашнього завдання у вигляді математичного або графічного диктанту, тестових завдань, а ⅔ частини уроку іде сприймання та усвідомлення нового матеріалу, шляхом пояснення вчителем теорії та розв’язування типових прикладів.
Урок систематизації і узагальнення вивченого матеріалу проходить як урок-семінар.
Далі йдуть урок контролю знань та урок аналізу контрольної роботи, на якому розглядаються прогалини в знаннях учнів з даної теми.
2. Короткий опис ІКТ, які можливо використати
при вивченні даного розділу
У пакет Microsoft Office для Windows входить додаток Power Point, який призначений для створення і редагування довільної презентації, що надають можливість поєднувати подання як аудіо- так і візуальної інформації.
Створені презентації можуть містити текст, фотознімки, діаграми, малюнки, комп’ютерну анімацію процесів та явищ, звуковий супровід, автофігури, діаграми тощо.
Об’єктом обробки Power Point є слайди разом з додатковою інформацією.
Основні можливості програми:
- створення послідовності слайдів;
- форматування тексту;
- вставляння гіперпосилань;
- вставляння керуючих кнопок;
- сортування слайдів;
- створення ефектів анімації та 3D-переходів слайдів;
- демонстрація презентації
Порядок розробки презентацій Створення будь-якої презентації звичайно включає три основні етапи:
- Проектування презентації.
- Створення запланованих слайдів.
- Встановлення послідовності слайдів та демонстрація презентації.
Слайди не мають бути перевантажені ані текстовою, ані графічною інформацією.
Додаткові вимоги до змісту презентації :
- Кожен слайд має відображати одну думку.
- Текст має складатися з коротких слів та простих речень.
- Рядок має містити 6-8 слів.
- Всього на слайді має бути 6-8 рядків.
- Загальна кількість слів не повинна перевищувати 50.
- Дієслова мають бути в одній часовій формі.
- Заголовки мають привертати увагу аудиторії та узагальнювати основні положення слайда.
- У заголовках мають бути і великі, і малі літери.
- Слайди мають бути не надто яскравими – зайві прикраси лише створюють бар’єр на шляху ефективної передачі інформації.
- Кількість блоків інформації під час відображення статистичних даних на одному слайді має бути не більше ніж чртири.
- Підписи до ілюстрації розміщуються під нею, а не над нею.
- Усі слайди презентації мають бути витримані в одному стилі.
Порядок редагування, форматування інформації такий же, як і у інших додатках пакету Microsoft Office.
Українська програма Gran призначена для графічного аналізу функцій. Основні функціональні можливості програми: побудова графіків функцій, обчислення значень функції в заданих точках, графічне розв’язання рішення рівнянь, систем рівнянь, нерівностей і систем нерівностей. Також програма дозволяє обчислювати об’єми і площі тіл обертання. Використання програми дає можливість значно інтенсифікувати процес навчання.
Програма Derive призначена для розв’язування досить значного кола математичних задач – відшукання розв’язків рівнянь в числових і буквених виразах, границь функцій, звичайних і частинних похідних різних порядків, розкладу функції в ряд Тейлора, невизначених та визначених інтегралів різної кратності зі сталими та змінними межами, виконання операцій над векторами та матрицями, визначення числових характеристик статистичних вибірок, графічних побудов у двовимірному і тривимірному просторах тощо. Крім того, виконуються спрощення виразів алгебраїчно з використанням досить загальних перетворень, обчислення значень виразів з вказаною точністю та ін.
Mathcad – програмний засіб, середовище для виконання на комп’ютері різноманітних математичних та технічних розрахунків, забезпечена простим в освоєнні і в роботі графічним інтерфейсом, яка надає користувачеві інструменти для роботи з формулами, числами, графіками та текстами. У середовищі Mathcad доступні більше сотні операторів та логічних функцій, призначених для чисельного і символьного розв’язування математичних задач різної складності. Mathcad є інтегрованою системою рішення математичних, інженерно-технічних і наукових завдань. Він містить текстовий і формульний редактор, обчислювач, засоби наукової і ділової графіки, а також величезну базу довідкової інформації, як математичної, так і інженерної, оформленої у вигляді вбудованого в Mathcad довідника.
Текстовий редактор служить для введення і редагування текстів. Тексти є коментарями, і вхідні в них математичні вирази не виконуються. Текст може складатися з слів, математичних символів, виразів і формул.
Формульний процесор забезпечує природний «багатоповерховий» набір формул у звичній математичної нотації (ділення, множення, квадратний корінь, інтеграл, сума і т.д.). Остання версія Mathcad повністю підтримує букви кирилиці в коментарях, формулах і на графіках.
Обчислювач забезпечує обчислення за складними математичними формулами, має великий набір вбудованих математичних функцій, дозволяє обчислювати ряди, суми, добутки, інтеграли, похідні, працювати з комплексними числами, розв’язувати лінійні і нелінійні рівняння, а також диференціальні рівняння та системи, проводити мінімізацію і максимізацію функцій, виконувати векторні і матричні операції, статистичний аналіз і т.д. У Mathcad вбудовані засоби символьної математики, що дозволяють розв’язувати задачі через комп’ютерні аналітичні перетворення.
Графічний процесор служить для створення графіків і діаграм. Він поєднує простоту спілкування з користувачем з великими можливостями засобів ділової та наукової графіки. Графіка орієнтована на розв’язання типових математичних задач. Можливо швидка зміна виду і розміру графіків, накладення на них текстових написів і переміщення їх у будь-яке місце документа.
Тестування як засіб педагогічної діагностики, дозволяє оперативно і точно визначити рівень знань окремого учня, характеристики навчального процесу в класі, групі, паралелі класів, школі, місті, країні.
Для комп’ютерного тестування знань та навичок учнів використовується контрольно-діагностична система Test‑W2. Отримавши на екрані питання, учневі потрібно клацнути на відповідях, які він вважає правильними. Результат відповіді негайно позначається (при закритому тестуванні – не позначається!) на полі ліворуч значками: – правильно; – неправильно. Праворуч на екрані знаходиться діаграма, що показує поточну оцінку і виражене у відсотках відношення кількості правильних відповідей до загальної кількості питань, на які відповів учень. Оцінка і це відношення з кожною правильною відповіддю учня збільшуються, доки не набудуть остаточного значення після відповіді на останнє запитання. Після завершення тестування прізвище і клас учня, дата, час і одержана оцінка заносяться у файл протоколу. Система Test‑W2 передбачає роботу у локальній мережі, зберігає протокол результатів тестування, має засоби для створення нових і редагування наявних тестів.
MyTestX – це потужний комплекс програм для підготовки та проведення комп’ютерного тестування. За допомогою програми MyTestX можлива організація і проведення тестування, іспитів в будь-яких освітніх установах (вузи, коледжі, школи) як з метою виявити рівень знань з будь-яких навчальних дисциплін, так і з навчальними цілями. Підприємства та організації можуть здійснювати атестацію та сертифікацію своїх співробітників.
MyTestX це – система програм (програма тестування учнів, редактор тестів і журнал результатів) для створення і проведення комп’ютерного тестування, збору та аналізу результатів, виставлення оцінки за вказаною в тесті шкалою. Програма легка і зручна у використанні. Всі вчителі та учні швидко і легко освоюють її.
Програма MyTestX працює з десятьма типами завдань: одиночний вибір, множинний вибір, встановлення порядку проходження, встановлення відповідності, вказівка істинності чи хибності тверджень, ручне введення числа, ручне введення тексту, вибір місця на зображенні, перестановка букв, заповнення пропусків (MyTestXPro). У тесті можна використовувати будь-яку кількість будь-яких типів, можна тільки один, можна і все відразу. У завданнях з вибором відповіді (одиночний, множинний вибір, вказівка порядку, вказівку істинності) можна використовувати до 10 (включно) варіантів відповіді.
3. Методика викладання теми «Тригонометричні
рівняння та нерівності» з використанням ІКТ
Однією з найскладніших тем шкільного курсу алгебри та початків аналізу є «Тригонометричні рівняння». Учням досить важко обрати правильний спосіб розв’язання того чи іншого тригонометричного рівняння. Вони допускають значну кількість помилок, тому важливо виконати ретельний аналіз кожної помилки. Для цього можна застосовувати такі програмні засоби, як Microsoft Power Point, Derive, Gran1, Mathcad, TEST-W і MyTestХ.
3.1. Використання презентацій Microsoft PowerPoint. Програма для створення презентацій Microsoft Power Point є універсальним видом наочності і може бути застосованою у будь-якому класі на уроці будь-якого типу. Та найефективнішою є підготовка та використання презентацій на таких етапах вивчення математики:
- уроки-лекції для пояснення нової теми, де учні не тільки слухають, продивляються інформацію на екранах, конспектують, а й відповідають на запитання, розв’язують задачі за наведеним зразком;
- для контролю набутих теоретичних знань: на екрані містяться запитання з наступною появою правильної відповіді для самоконтролю;
- для виконання тестових завдань з наступною появою правильної відповіді після його виконання;
- для проведення усного рахунку;
- інтегровані уроки математики з іншими предметами;
- уроки-подорожі та інше.
Прикладом демонстраційного супроводу під час пояснень на уроці є презентація теми «Тригонометричні рівняння та нерівності». Пояснення учителя супроводжується інформацією на слайдах, що є не тільки яскравою динамічною ілюстрацією, а й способом фіксації найсуттєвішого у новому матеріалі. Перший приклад розв’язування тригонометричного рівняння чи нерівності вчитель пояснює сам, для другого – залучає учнів до пояснень за готовим малюнком. Для прикладу надані слайди презентацій розв’язування тригонометричних рівнянь та нерівностей.
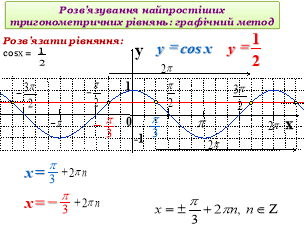
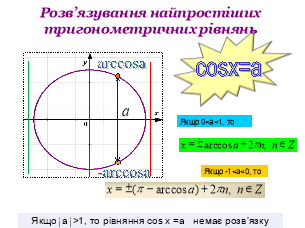
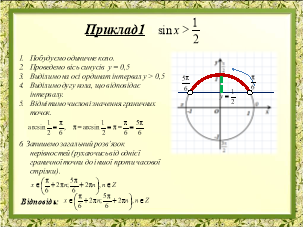
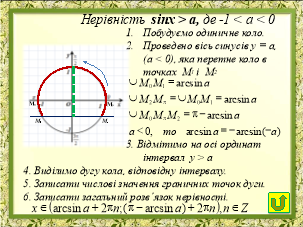




Досить ефективно використовувати слайди для проведення тестування з наступною появою правильних варіантів відповідей після їх виконання. На екран проектується тест, після виконання якого учні обмінюються зошитами і здійснюють взаємоперевірку.
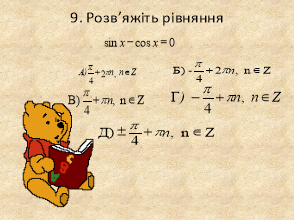



Систематичне використання комп’ютерних презентацій на уроках знімає актуальне питання наочності з математики. Більше того, постає інше питання – чи варто витрачати й так невеликі шкільні ресурси для придбання наочності, зокрема традиційних таблиць, плакатів тощо, якщо можна подати їх у вигляді презентації.
3.2. Використання Gran1. У процесі розв’язування тригонометричних рівнянь можуть виконуватись перетворення, що призводять до появи сторонніх коренів чи втрати коренів. У такому разі необхідно виконати відбір коренів тригонометричного рівняння, саме на цьому етапі учні допускають значну кількість помилок.
Приклад 1. Розглянемо тригонометричне рівняння sin x – cos x = 1. Як показує досвід, учні частіше розв’язують його способом зведення до однієї тригонометричної функції, а не за допомогою формули синуса різниці.
Перепишемо рівняння так: sin x = 1 + cos x. Оскільки
sin x = ![]() ,
,
то
![]() .
.
Піднесемо обидві частини отриманого рівняння до квадрата. Маємо:
![]() = 1 + 2cos x +
= 1 + 2cos x + ![]() ,
,
або
cos x (cos x + 1) = 0.
Отримаємо сукупність:
![]()
Розв’язками цієї сукупності є:
x = ![]() +
+ ![]() ; х =
; х = ![]() ; х =
; х = ![]() +
+ ![]() .
.
На цьому етапі учні записують відповідь, забуваючи, що треба зробити перевірку, бо можуть з’явитися сторонні корені під час піднесення обох частин рівняння до квадрату.
-
Якщо x =
 +
+ 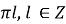 , то sin (
, то sin ( +
+ 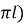 – cos (
– cos ( +
+ 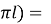 sin
sin – cos
– cos = 1.
= 1.
-
Якщо
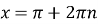 , то
, то 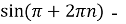 cos
cos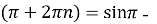 cos
cos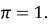
-
Якщо
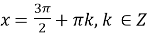 , то
, то 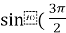 +
+ 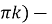 cos
cos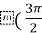 +
+ 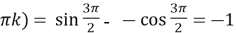 . Отже, х =
. Отже, х = 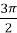 +
+ 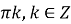 – сторонній корінь.
– сторонній корінь.
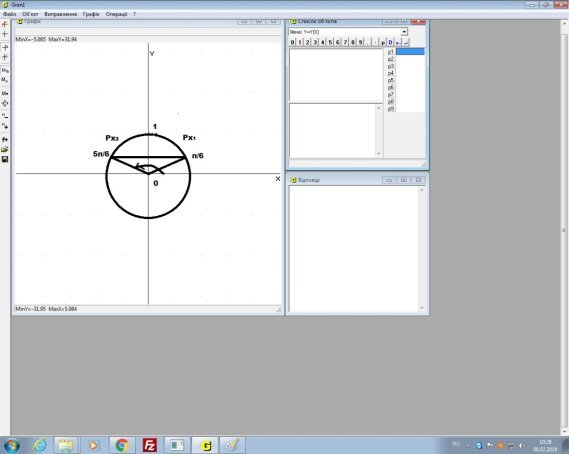
Тому доцільно разом з учнями виконати графічну перевірку розв’язання даного рівняння за допомогою Gran1.
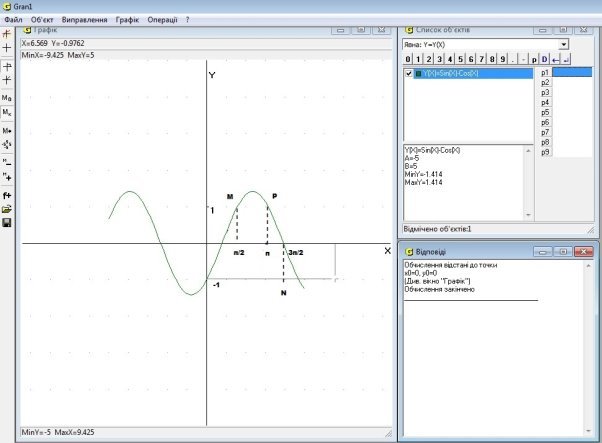
Як видно на малюнку т.М (![]() належить графіку, т.Р (
належить графіку, т.Р (![]() теж належить графіку. А т.N (
теж належить графіку. А т.N (![]() не належить графіку, отже, не є розв’язком рівняння sin x – cos x = 1.
не належить графіку, отже, не є розв’язком рівняння sin x – cos x = 1.
Приклад 2. Розв’яжіть нерівність sinx > ![]() . за допомогою програми Gran1.
. за допомогою програми Gran1.
Оскільки sin x — це ордината відповідної точки ![]() одиничного кола, то при всіх значеннях x, які задовольняють даній нерівності, точка
одиничного кола, то при всіх значеннях x, які задовольняють даній нерівності, точка ![]() має ординату, більшу за
має ординату, більшу за![]() . Усі такі точки на одиничному колі лежать вище за пряму y =
. Усі такі точки на одиничному колі лежать вище за пряму y = ![]() (вони зображені на рисунку синьою дугою
(вони зображені на рисунку синьою дугою ![]() без крайніх точок, оскільки в крайніх точках sin x =
без крайніх точок, оскільки в крайніх точках sin x =![]() , а не більший за
, а не більший за ![]() ). Якщо, записуючи відповідь, рухатися проти годинникової стрілки, то точка
). Якщо, записуючи відповідь, рухатися проти годинникової стрілки, то точка ![]() буде початком дуги
буде початком дуги ![]() , а точка
, а точка ![]() — її кінцем. Спочатку запишемо відповідь на одному періоді (нагадаємо, що для синуса період дорівнює 2π). Для точок
— її кінцем. Спочатку запишемо відповідь на одному періоді (нагадаємо, що для синуса період дорівнює 2π). Для точок ![]() виділеної дуги
виділеної дуги ![]() < x <
< x <![]() . Оскільки точка
. Оскільки точка ![]() знаходиться в правій півплощині, то можна взяти
знаходиться в правій півплощині, то можна взяти ![]() = arcsin
= arcsin![]() =
= ![]() . Тоді
. Тоді ![]() = π −
= π − ![]() =
= ![]() . Таким чином, на одному періоді розв’язками заданої нерівності є:
. Таким чином, на одному періоді розв’язками заданої нерівності є: ![]() < x <
< x < ![]() . Через період 2π значення синуса повторюються, отже, всі інші розв’язки заданої нерівності отримуємо додаванням до знайдених розв’язків чисел виду 2πk, де k ∈ Z. Одержуємо відповідь:
. Через період 2π значення синуса повторюються, отже, всі інші розв’язки заданої нерівності отримуємо додаванням до знайдених розв’язків чисел виду 2πk, де k ∈ Z. Одержуємо відповідь: ![]() +2πk < x <
+2πk < x < ![]() + 2πk, k∈Z.
+ 2πk, k∈Z.
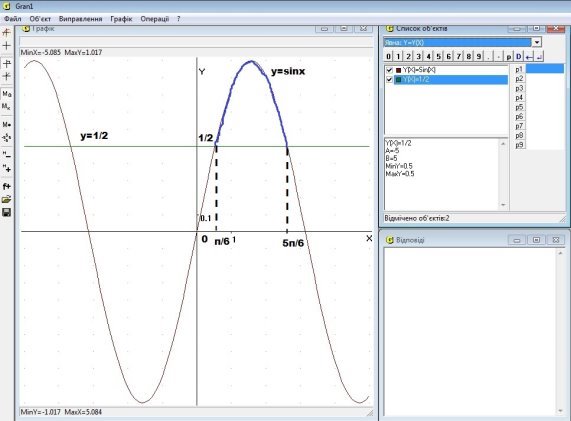
Для розв’язування нерівності sin x >![]() можна скористатися також графіками функцій y = sin x та y =
можна скористатися також графіками функцій y = sin x та y =![]() (рис.).
(рис.).
Розв’язками нерівності sin x >![]() будуть ті і тільки ті значення x, для яких відповідні точки графіка функції y = sin x знаходяться вище прямої y =
будуть ті і тільки ті значення x, для яких відповідні точки графіка функції y = sin x знаходяться вище прямої y =![]() (на рисунку відповідні частини графіка функції виділено синіми лініями).
(на рисунку відповідні частини графіка функції виділено синіми лініями).
Щоб знайти абсциси точок перетину цих графіків, досить розв’язати рівняння sin x =![]() (х=
(х=![]() )
) ![]() + πn n∈Z). Враховуючи періодичність функції sin x (T = 2π), досить записати розв’язок заданої нерівності на одному періоді. На відрізку довжиною 2π можна взяти, наприклад, такі абсциси точок перетину графіків функцій y = sin x і y =
+ πn n∈Z). Враховуючи періодичність функції sin x (T = 2π), досить записати розв’язок заданої нерівності на одному періоді. На відрізку довжиною 2π можна взяти, наприклад, такі абсциси точок перетину графіків функцій y = sin x і y =![]() :
: ![]() =
= ![]() ,
, ![]() =
=![]() (усі інші абсциси точок перетину відрізняються від них на 2πk). Тоді на одному періоді розв’язками заданої нерівності є:
(усі інші абсциси точок перетину відрізняються від них на 2πk). Тоді на одному періоді розв’язками заданої нерівності є: ![]() < x <
< x < ![]() (абсциси виділених точок графіка y = sin x). Усі інші розв’язки заданої нерівності одержуються додаванням до знайдених чисел виду 2πk, де k ∈ Z. Знову одержуємо відповідь:
(абсциси виділених точок графіка y = sin x). Усі інші розв’язки заданої нерівності одержуються додаванням до знайдених чисел виду 2πk, де k ∈ Z. Знову одержуємо відповідь: ![]() +2πk < x <
+2πk < x < ![]() + 2πk, k∈Z.
+ 2πk, k∈Z.
3.3. Використання Derive. При розв’язуванні (з використанням послуги soLve) найпростіших тригонометричних рівнянь виду sin(x) = а, cos(x) = а, tg(x) = а, ctg(x) = а за допомогою програми Derive подаються головні розв’язки цих рівнянь у вигляді, показаному на малюнку.
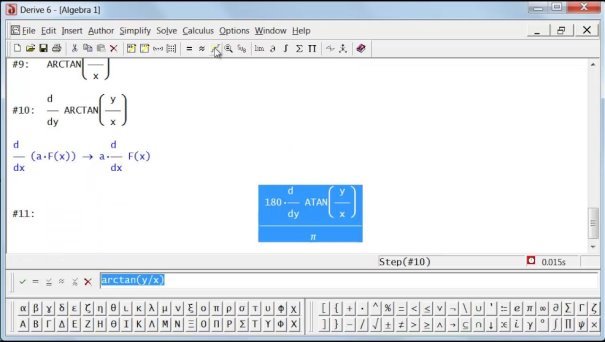
Інші розв’язки можна отримати , використовуючи відповідні графічні побудови або ж враховуючи властивості функцій sin(x), cos(x), tg(x), ctg(x) (парність чи непарність, періодичність, величину періоду, відомості про межі, в яких слід визначити значення х). Якщо програма не знаходить розв’язків рівняння, на екран виводиться вихідне рівняння в незмінному вигляді.
Приклад 1. Знайти розв’язки рівняння sin(x) + cos(2x) = 1.
Звернення до послуги soLve не дає бажаних результатів, хоч, очевидно, рівняння має розв’язки. Якщо в підпункті Trigonometry пункту Manage встановити: Direction: Expand і Toward: Sines, вказаний вираз набуде вигляду ![]() (див. рис.), однак подальше звернення до послуги soLve, послуг Simplify чи Expand бажаних результатів не дає. В такому разі слід позначити
(див. рис.), однак подальше звернення до послуги soLve, послуг Simplify чи Expand бажаних результатів не дає. В такому разі слід позначити ![]() через, наприклад, v і ввести до розгляду рівняння виду
через, наприклад, v і ввести до розгляду рівняння виду ![]() . Після звернення до пункту soLve одержимо:
. Після звернення до пункту soLve одержимо: ![]() ,
, ![]() Розв’язуючи тригонометричні рівняння sin(x) = 0 та sin(x) =
Розв’язуючи тригонометричні рівняння sin(x) = 0 та sin(x) = ![]() , одержимо розв’язки вихідного тригонометричного рівняння:
, одержимо розв’язки вихідного тригонометричного рівняння: ![]() ,
, ![]() + 2k
+ 2k![]() ,
, ![]() Z .
Z .
У попередньому прикладі було введено заміну ![]() sin(x) (після того, як cos(2x) було подано через
sin(x) (після того, як cos(2x) було подано через ![]() cos(2x) =
cos(2x) = ![]() .
.
Часто зручно тригонометричне рівняння звести до алгебраїчного, скориставшись заміною ![]() tg(
tg(![]() ). Тоді
). Тоді
cos(x) = 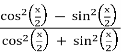 =
= 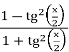 =
= ![]() ,
,
sin(x) = ![]() =
= ![]() =
= ![]() .
.
Розв’язавши (якщо вдається) отримане алгебраїчне рівняння відносно ![]() і скориставшись оберненою заміною х = 2arctg(
і скориставшись оберненою заміною х = 2arctg(![]() , можна знайти розв’язок вихідного тригонометричного рівняння.
, можна знайти розв’язок вихідного тригонометричного рівняння.
Приклад 2. Знайти розв’язки рівняння sin(x) + sin(x) cos(x)+ cos(x) = 0.
Безпосереднє звернення до послуги soLve не дає результатів.
Поклавши ![]() tg(
tg(![]() ), одержимо
), одержимо
![]() +
+![]() +
+![]() =0,
=0,
![]() +
+![]() =0,
=0,
![]() +
+![]() =0,
=0,
![]() +1-
+1-![]() =0,
=0, ![]() -4
-4![]() -1=0.
-1=0.
Використання послуги soLve не дає бажаних результатів.
Побудувавши графік функції у = ![]() -4
-4![]() -1, бачимо, що рівняння
-1, бачимо, що рівняння ![]() -4
-4![]() -1=0 має два дійсні корені:
-1=0 має два дійсні корені: ![]() -0,249,
-0,249, ![]() 1,663.
1,663.
Враховуючи, що х=2arctg![]() , одержимо
, одержимо ![]() -0,488
-0,488 ![]() 2k
2k![]() 3,088
3,088 ![]() 2k
2k![]() , k=0,1,2,…
, k=0,1,2,…
3.4. Використання Mathcad. Для аналітичного розв’язання рівнянь в системі MathCad є спеціальний оператор Solve (Розв’язати) панелі Symbolic (Символьні). Для того щоб знайти корені рівняння за допомогою оператора Solve потрібно:
1. Ввести оператор Solve з панелі Symbolic.
2. В лівому маркері задати вид рівняння, яке потрібно розв’язати. В якості „=” потрібно ввести знак рівності з панелі Boolean (Ctrl+”=”). Також в лівий маркер можна вводити ім’я функції. У цьому випадку програма знайде нулі функції. Форма запису рівняння через функцію зручне у випадку, коли вона має велику довжину.
3. В правий маркер ввести змінну, відносно якої потрібно виконати розв’язання рівняння. Якщо рівняння має декілька розв’язків, то оператор Solve подає результат у вигляді вектора (матриці-стовпця).
Розв’язування тригонометричних рівнянь
Як відомо, більшість тригонометричних рівнянь мають нескінченну кількість коренів, які записуються за допомогою спеціальних виразів, наприклад: корені рівняння sin(x) = 0 мають вигляд π + πk, (де k Z). MathCad знаходить корені лише на проміжку одного періоду функції, заданої в рівнянні. Також, MathCad досить часто робить помилки у розв’язанні тригонометричних рівнянь, особливо, якщо таке рівняння містить параметри. Тому на практиці краще будувати графіки таких рівнянь, або намагатися максимально спростити рівняння.
Приклад 1. Розв’язати рівняння cos(2x)=0 на проміжку від 0 до![]() .
.
При чисельному розв’язанні рівнянь бажано завжди будувати графік функції. Це допоможе уникнути помилок і правильно визначити потрібний інтервал локалізації коренів. Побудуємо графік нашої функції:
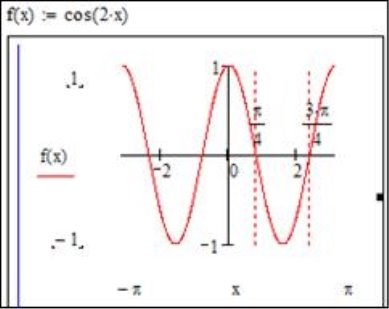
Змінимо межі по ОХ від (-π;π) для зручності. Поставимо маркери в точках ![]() та
та ![]() . Очевидно, що всі корені цього рівняння рівняння мають вигляд:
. Очевидно, що всі корені цього рівняння рівняння мають вигляд: ![]() , де R – множина цілих чисел. Подивимось, чи знайде функція rootкорені даного рівняння на вказаному проміжку.
, де R – множина цілих чисел. Подивимось, чи знайде функція rootкорені даного рівняння на вказаному проміжку.
![]()
Корінь визначено вірно.
Приклад 2. Розв’язати рівняння cos(x)=х+0,2 за допомогою функції root.

Приклад 3. При розв’язуванні рівнянь з тангенсами и котангенсами виникає вцілому здійсненна проблема, пов'язана з тим, що дані функції визначені не у всіх точках числової прямої.
.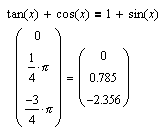
Даний приклад показує, що вищевказане обмеження не грає особливої ролі при вирішенні рівнянь за допомогою MathCAD. Оскільки синус і косинусвизначені для всіх значень аргументу, питання про область визначення привирішенні рівнянь, що містять тільки ці тригонометричні функції, як правило, відпадає.
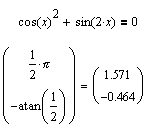
Замість цього виникає інша складність: зворотні функції asin (x) і acos (x), значеннями яких є головні значення зворотних відображень, не дають усіх розв’язків в рамках одного періоду (2p).
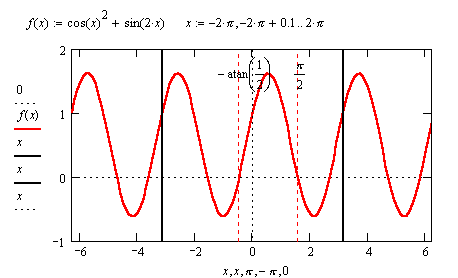
Оскільки залишається неясним, яке саме з значень зворотного відображення MathCAD розглядає в якості головного при вирішенні рівнянь, виявляється складно отримати ще одне значення, віддалені від головного менш ніж на період; тим самим завдання було б вирішена з точністю до періоду. У подібних ситуаціях на виручку приходить побудова графіків.
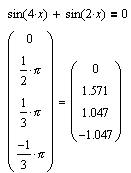
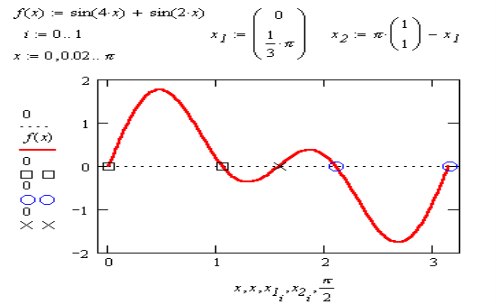
Даний приклад демонструє межі можливості MathCAD. Рішення в лоб не дає ніяких результатів.
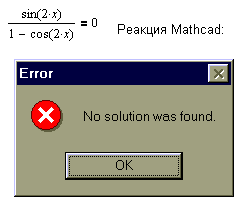
Провівши додаткові перетворення, все-таки вдається знайти розв’язок.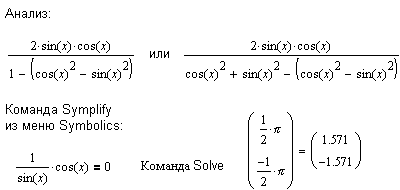
Приклад 4. Розв’язати нерівність 2![]() (x) – sin(x) + sin(3x)
(x) – sin(x) + sin(3x) ![]() 1.
1.
Спроба розв’язати її напряму буде невдалою. Тому, необхідно розв’язувати по крокам. Для початку приведемо вираз до одного аргументу. Для цього потрібно подати sin(3x) через синус и косинус від х. Виконати це перетворення дозволяє оператор expand.
2![]() (x)– sin(x) + sin(3x) expand, х
(x)– sin(x) + sin(3x) expand, х ![]() 2
2![]() – 2sin(x) + 4sin(x)
– 2sin(x) + 4sin(x)![]()
Отриманий вираз має синуси та косинуси. Щоб подалі його можна було розглядати як алгебраїчний, потрібно залишити в ньому лише один вид функції. Простіше позбутися від косинусів. Підставимо отриманий вираз в нерівність (оператор substitute), а потім спростимо його.
![]()
Далі потрібно, розв’язавши отриману нерівність відносно sin(x), визначити при яких значеннях синуса вона виконується.
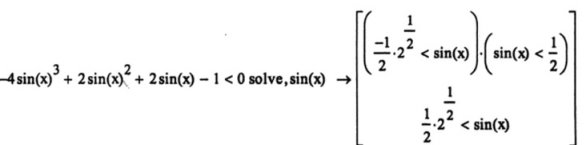
Отже, розв’язана нерівність правильна, якщо sin(x)![]() (-
(-![]() /2; ½)
/2; ½) ![]() (
(![]() /2; 1). Щоб знайти, яким повинен бути х, щоб ця умова виконувалась, проаналізуємо графік синуса на проміжку одного періода.
/2; 1). Щоб знайти, яким повинен бути х, щоб ця умова виконувалась, проаналізуємо графік синуса на проміжку одного періода.
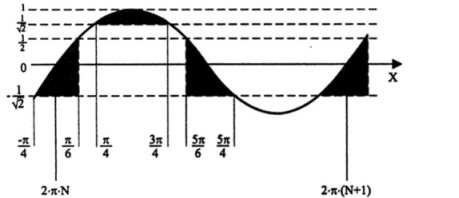
Відмітивши на вісі Y межі областей розв’язку, проведемо допоміжні лінії. Укладені між ними фрагменти кривої мають точки, які задовольняють нерівність. Таких фрагментів на проміжку періоду три. Дивлячись на отриману схему, зовсім не складно знайти координати їх меж по Х і записати кінцеву відповідь![]() х
х![]() (-
(-![]()
3.5. Контрольно-діагностичні системи Test-W і MyTestХ. Тестові методики добре зарекомендували себе в багатьох країнах світу. А з урахуванням переходу у 2007 році на незалежне зовнішнє оцінювання навчальних досягнень випускників загальноосвітніх навчальних закладів потребують ширшого впровадження у практику роботи. Систематична робота з комп’ютерним тестом повинна стати для учня звичною справою. Тоді зростають його шанси на складання успішного незалежного зовнішнього тестування.
За допомогою ПК зручно проводити поточне оцінювання у вигляді тестів. Для цього можна використовувати програму створення тестів Test-W. Вихідний тест може мати будь-яку кількість питань (рекомендується від 30 до 50 і більше). З вихідного тесту методом випадкового вибору послідовно виводиться задана кількість питань (наприклад, 25). Таким чином, кожен учень одержує свій відмінний від сусідів набір питань, що забезпечує індивідуалізацію і об’єктивність оцінки. На кожне питання тесту пропонується 5 варіантів відповідей, серед яких від одного до трьох вірних. Учню треба вказати правильні, на його думку відповіді і перейти до наступного питання. Час відповіді на тест обмежений. Рекомендується проводити тестування на протязі 10-15 хвилин для кількості питань 20-25.
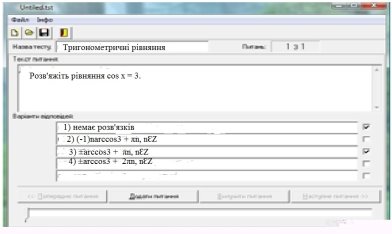
Система Test-W2 застосовується для контролю знань учнів там, де можна підготувати коротко сформульовані запитання й до кожного дати 2 – 5 варіантів відповідей (від 1 до 3 з яких правильні). Як питання, так і варіанти відповідей можуть мати вигляд тексту, формули, таблиці або малюнка.
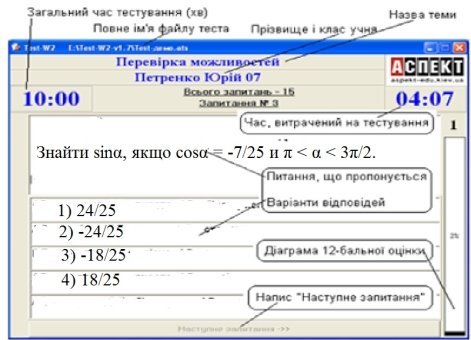
Оцінка виставляється відповідно до вибраної шкали згідно з відсотком правильних відповідей.
Оцінка 12 балів не ставиться, оскільки комп’ютерні тести не містять творчих завдань.
Нарахування балів
- запитання з однією правильною відповіддю: 0 або 1 бал;
- запитання з двома правильними відповідями: 0; 0,5 (одна правильна відповідь) або 1 бал;
- запитання з трьома правильними відповідями: 0; 0,33 (одна правильна відповідь); 0,67 (дві) або 1 бал.
Загальна оцінка за тест виставляється автоматично відповідно до вибраної шкали згідно з відсотком правильних відповідей.
Проведення тестування
Для проведення тестування потрібно виконати такі дії:
- завантажити файл Test-W2.exe одним із способів, що надає Windows;
- натиснути кнопку «Відкрити тест»;
- у вікні діалогу знайти та відкрити папку «Інформатика», а потім папку класу;
- знайти та відкрити файл потрібного тесту (наприклад, «Тема 3-7») – з’явиться діалогове вікно «Авторизація»;
- ввести з клавіатури своє прізвище, ім’я та клас, натиснути кнопку «ОК» – розпочнеться тестування.
Програма Test-W2 послідовно виводить на екран запитання вибраного тесту та пропонує на кожне до 5 варіантів відповідей, від 1 до 3 з яких правильні. Послідовність виведення на екран питань із тесту, розташування варіантів відповідей на сусідніх комп’ютерах різна. Отже, кожен учень одержує відмінну від сусідів послідовність запитань і варіантів відповідей. Ця відмінність тим більша, чим більша кількість завдань у банку цього тесту. Наприклад, тест має 32 запитання, а відповісти потрібно на 20. Варіантів із 32 елементів по 20 може бути безліч не тільки з різною послідовністю питань, а й з відмінностями в розташуванні відповідей.

Учневі потрібно послідовно клікнути 1, 2 або 3 варіанти відповідей, які він вважає правильними, доки не стане доступною кнопка «Наступне запитання» (почорніє напис). Для переходу до наступного запитання потрібно клікнути цю кнопку.
Якщо під час підготовки тесту у вікні редактора був встановлений прапорець «Діагностика», варіанти відповіді будуть негайно позначатися на полі ліворуч значками: – правильно; – неправильно.
Праворуч на екрані знаходиться діаграма, яка показує відсоток правильних відповідей від встановленої кількості завдань. Відповідно до цього відсотку виставляється оцінка за вибраною шкалою. Оцінка і це відношення з кожною правильною відповіддю учня збільшуються, доки не набудуть остаточного значення після відповіді на останнє запитання.
Питання, які залишилися без відповіді за браком часу, зараховуються як такі, на які отримано неправильні відповіді. Відповідно зменшується відсоток правильних відповідей та оцінка.
Після відповіді на останнє запитання замість напису «Наступне питання» з’явиться «Натисніть, щоб одержати кінцевий результат…», після кліку на ньому з’являється вікно з результатами тестування: кількість правильних відповідей, допущених помилок, шкала оцінювання та оцінка в балах.
Після проходження тесту прізвище, ім’я та клас учня, дата, час і одержана оцінка заносяться у протокол.
Після натискання на кнопку «Повідомте результат учителю!» всі вікна закриваються. Для нового тестування потрібно знову завантажити програму Test-W2 і повторити описані вище дії.
Для перегляду результатів тестування потрібно:
- завантажити файл Test-W2.exe;
- натиснути кнопку «Результати» – відкриється протокол результатів проведених тестувань наведеного вигляду;
- після перегляду закрити вікно.
Якщо тестування завершене примусово, то у протокол заноситься оцінка 0 балів.
Висновки
Отже, використання інформаційно-комунікаційних технологій на навчальних заняттях з алгебри сприяють активізації навчально-пізнавальної діяльності учнів, швидкому та ефективному засвоєнню ними навчального матеріалу, формуванню ключових компетенцій школяра.
Переваги використання ІКТ:
- Індивідуалізація навчання;
- Інтенсифікація самостійної роботи учнів;
- Зростання обсягу виконаних на урок завдань;
- Розширення інформаційних потоків при використанні Internet;
- Підвищення мотивації та пізнавальної активності за рахунок різноманітності форм роботи, можливості включення ігрового моменту.
Комп’ютер дає вчителю нові можливості, дозволяючи разом з учнем отримувати задоволення від захопливого процесу пізнання, не тільки силою уяви забираючи стіни шкільного кабінету, але за допомогою новітніх технологій дозволяє зануритися в яскравий барвистий світ. Таке заняття викликає у дітей емоційний підйом, навіть відсталі учні охоче працюють з комп’ютером.
Інтегрування звичайного уроку з комп’ютером дозволяє вчителю перекласти частину своєї роботи на ПК, роблячи при цьому процес навчання більш цікавим, різноманітним, інтенсивним. Зокрема, стає більш швидким процес запису визначень, теорем та інших важливих частин матеріалу, тому що вчителю не доводиться повторювати текст кілька разів (він вивів його на екран), учневі не доводиться чекати, поки вчитель повторить саме потрібний йому фрагмент.
Цей метод навчання дуже привабливий і для вчителів: допомагає їм краще оцінити здібності і знання дитини, зрозуміти його, спонукає шукати нові, нетрадиційні форми і методи навчання, стимулює його професійний ріст і все подальше освоєння комп’ютера.
Застосування на уроці комп’ютерних тестів і діагностичних комплексів дозволить вчителю за короткий час отримувати об’єктивну картину рівня засвоєння матеріалу, що вивчається у всіх учнів і своєчасно його скоректувати. При цьому є можливість вибору рівня складності завдання для конкретного учня.
Для учня важливо те, що відразу після виконання тесту (коли ця інформація ще не втратила свою актуальність) він отримує об’єктивний результат із зазначенням помилок, що неможливо, наприклад, при усному опитуванні.
На уроках математики, інтегрованих з інформатикою, учні оволодівають комп’ютерною грамотністю і вчаться використовувати на уроках один з найбільш потужних сучасних універсальних інструментів – комп’ютер, з його допомогою вони розв’язують рівняння, будують графіки, креслення, готують тексти, малюнки для своїх робіт.
Мій досвід роботи дає можливість оцінити ефективність використання ІКТ при контролі засвоєння пройдених тем математики в порівнянних значеннях (якість навчання, дані анкетування учнів і т.д.):
- підвищився інтерес учнів до вивчення математики – на 25%;
- збільшилася кількість учнів, що беруть участь у контролі знань, в 2 рази;
- якість навчання математики підвищилася на 10-15%;
- поряд із цим можливості ІКТ використовуються для розвитку пам’яті учнів, розвитку вмінь організації навчальної праці, уміння знаходити необхідну інформацію за допомогою ІКТ, формування логічного, абстрактного й системного мислення, формування розумових операцій – аналізу, узагальнення, доведення, класифікації тощо.
Це можливість для учнів проявити свої творчі здібності. Але, поряд з плюсами, виникають різні проблеми як при підготовці до таких уроків, так і під час їх проведення.
Література
- Нелін Є. П. Алгебра і початки аналізу: Дворівневий підруч. для 10 кл. загальноосвіт. навч. закладів. – Х.: Світ дитинства, 2004. – 432 с.
- Бескин Н. М. Задачник-практикум по тригонометрии. – М.: УЧПЕДГИЗ, 1962. – 185 с.
- Панчишкин А. А., Шевгуладзе Е. Т. Тригонометрические функции в задачах. – М.: Наука, 1986. – 160 с.
- Жалдак М. І. Комп’ютер на уроках математики. Посібник для вчителів. Видання 2-ге, перероблене та доповнене – К.: РННЦ “Дініт”, 2003. – 324 с.
- Пометун О. І., Пироженко Л. В. Сучасний урок. Інтерактивні технології навчання: Наук.-метод. посібник. – К.: Вид-во А.С.К., 2003. – 192 с.
- Mathcad у дослідженні технічних систем: Навч. посібник / В.П. Франчук, К. С. Заболотний, О. Л. Жупієв, М. В. Полушина, О.В. Анциферов. – Дніпропетровськ: Національний гірничий університет, 2004.
- Д.Гурский, Е.Турбина Вычисления в Mathcad 12 – СПб: Питер. 2006. – 544 с.
- Сдвижков О. А. Энциклопедия компьютерной математики: старшеклассникам Часть 2, 25 стр.
- http://shkola.ostriv.in.ua/publication/code-38D98DDA09CC5/list-BB03C82726 (Програма TEST-W О. Шестопалова)
- http://www.mon.gov.ua/education/average
- http://mytest.klyaksa.net/htm/index.htm
1


про публікацію авторської розробки
Додати розробку


