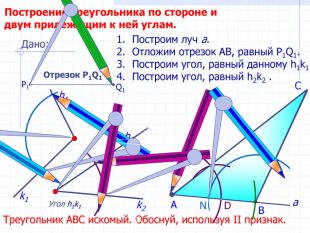
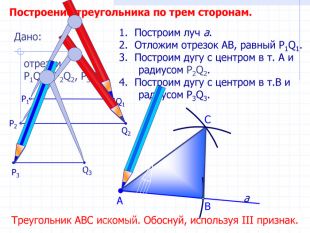
Задачи на построение 7 класс, геометрия

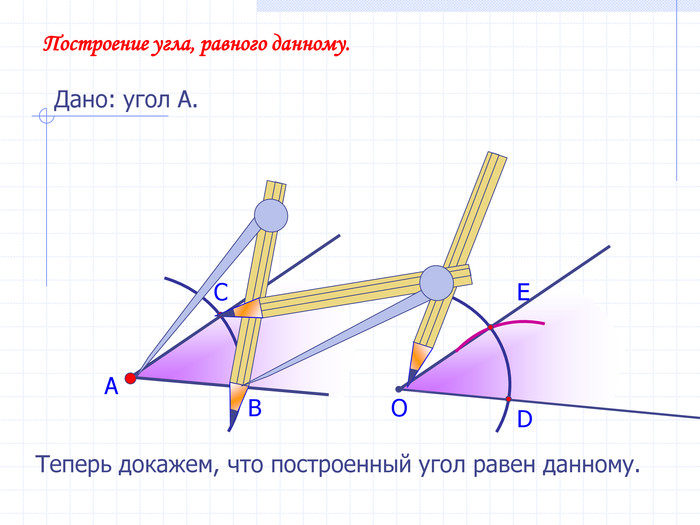
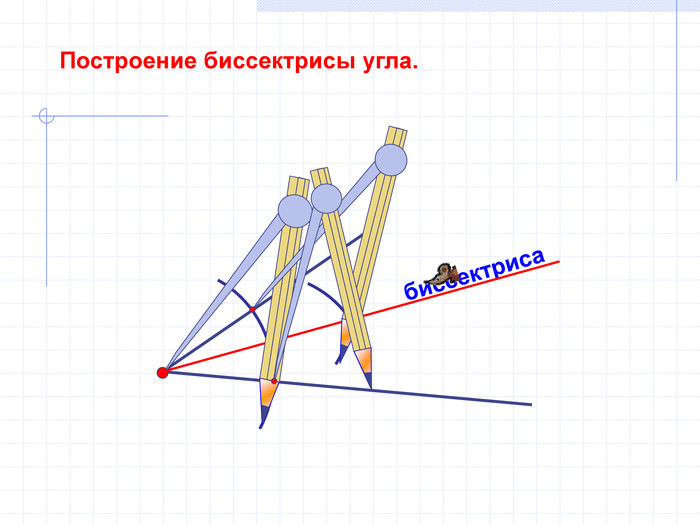
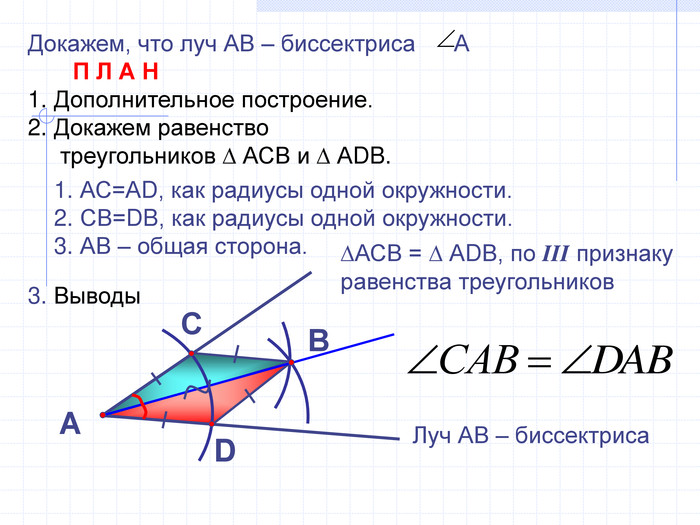
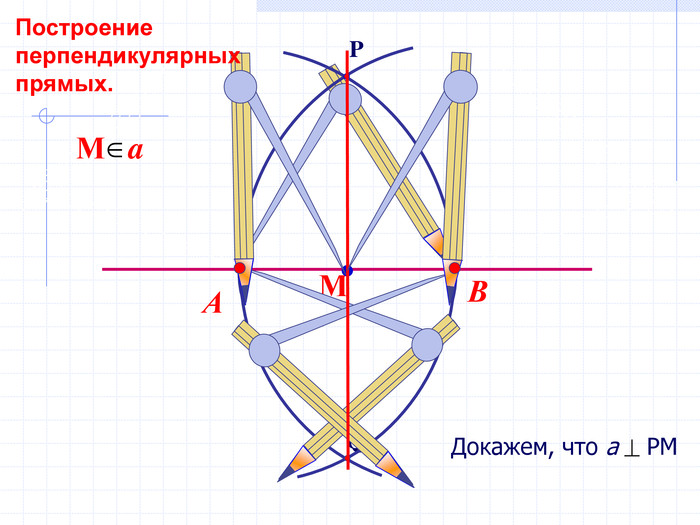
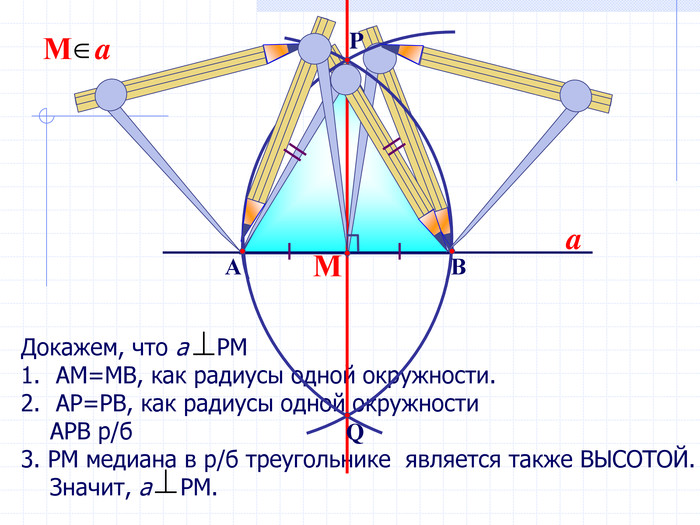
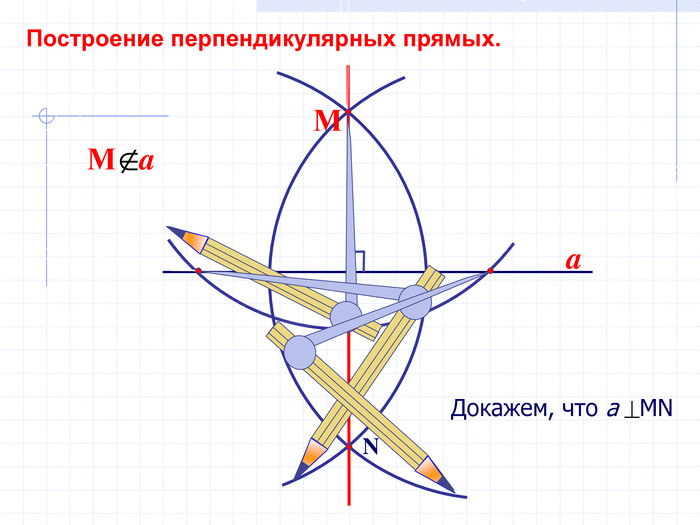
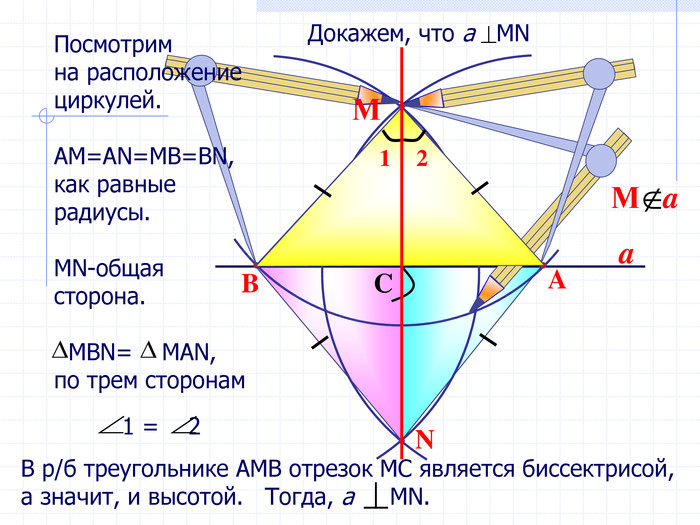
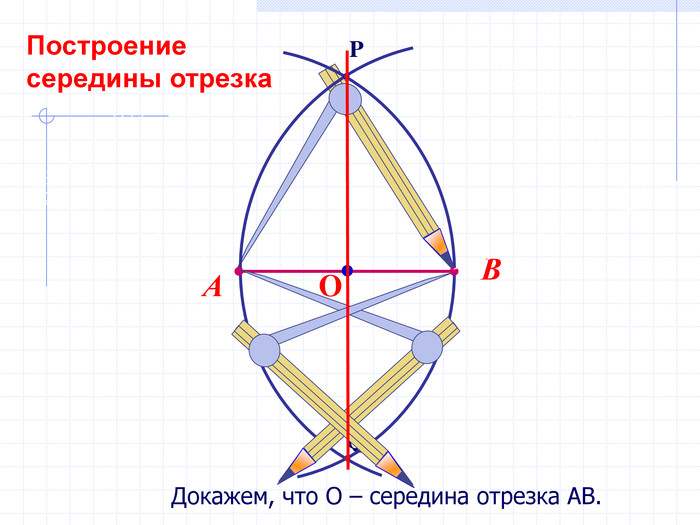
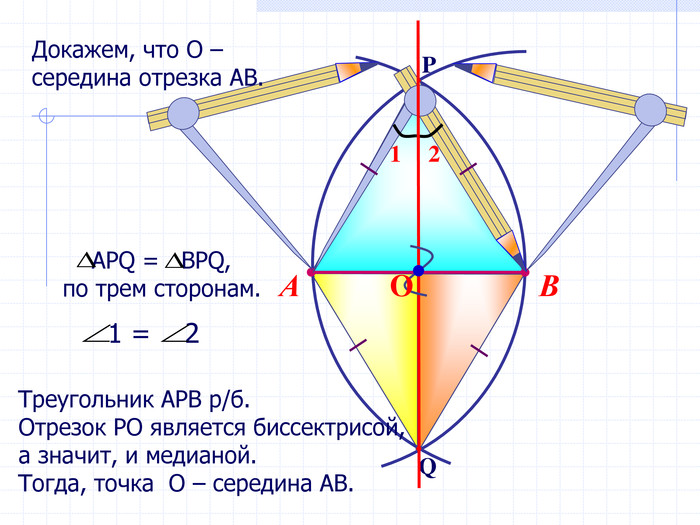
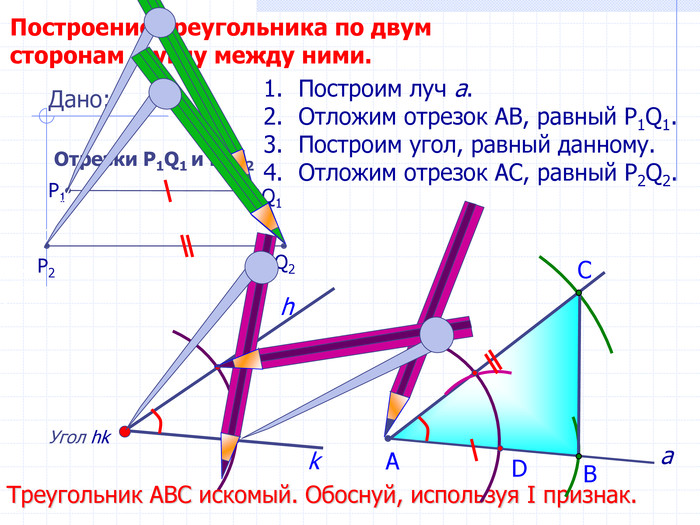
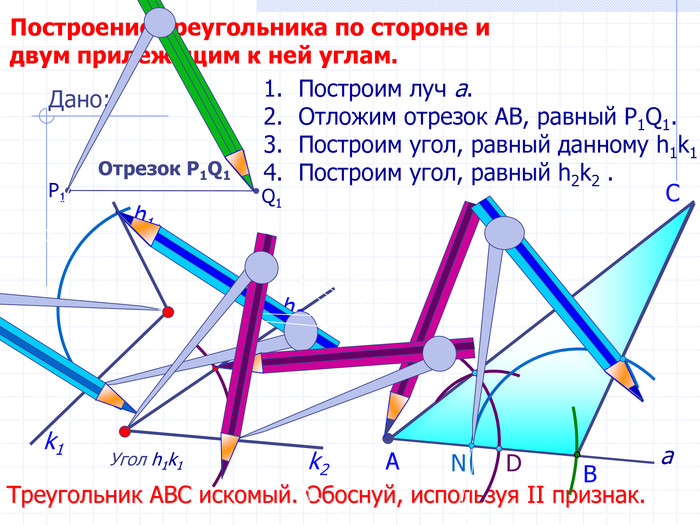
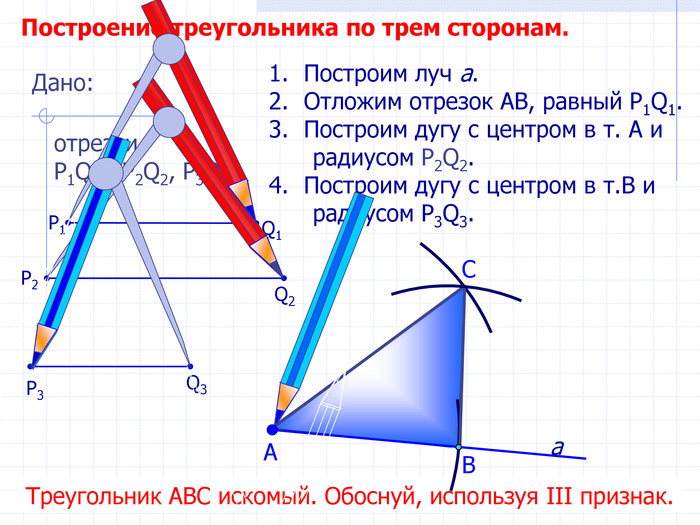
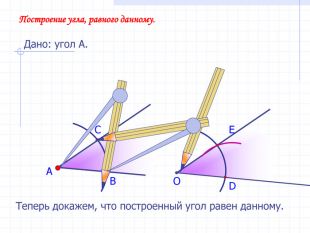
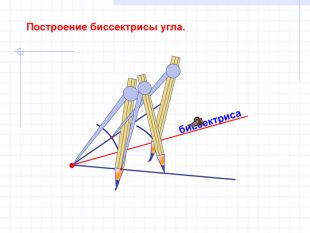
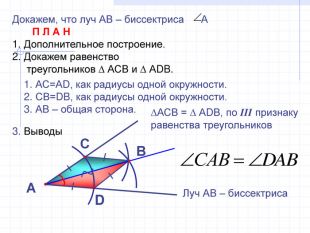
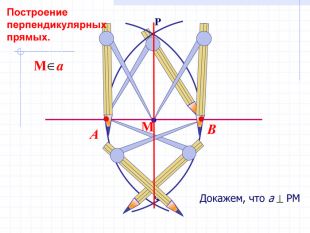
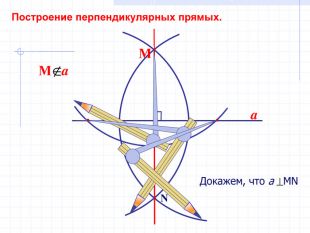
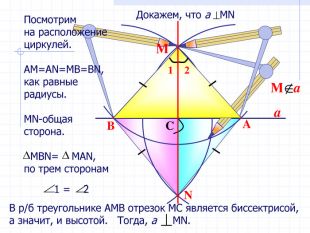
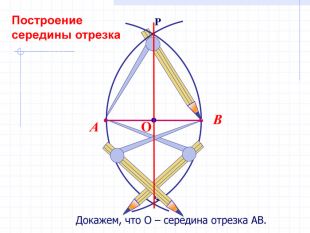
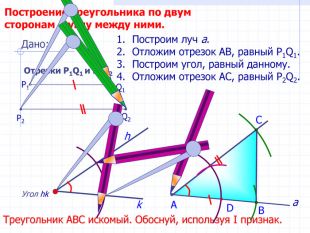
В геометрии выделяют задачи на построение, которые можно решить только с помощью двух инструментов: циркуля и линейки без масштабных делений. Линейка позволяет провести произвольную прямую, а также построить прямую, проходящую через две данные точки; с помощью циркуля можно провести окружность произвольного радиуса, а также окружность с центром в данной точке и радиусом, равным данному отрезку. IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

А В С Построение угла, равного данному. Дано: угол А. О D E Теперь докажем, что построенный угол равен данному.

Построение угла, равного данному. Дано: угол А. А Построили угол О. В С О D E Доказать: А = О Доказательство: рассмотрим треугольники АВС и ОDE. АС=ОЕ, как радиусы одной окружности. АВ=ОD, как радиусы одной окружности. ВС=DE, как радиусы одной окружности. АВС= ОDЕ (3 приз.) А = О

биссектриса Построение биссектрисы угла.

Докажем, что луч АВ – биссектриса А П Л А Н Дополнительное построение. Докажем равенство треугольников ∆ АСВ и ∆ АDB. 3. Выводы А В С D АС=АD, как радиусы одной окружности. СВ=DB, как радиусы одной окружности. АВ – общая сторона. ∆АСВ = ∆ АDВ, по III признаку равенства треугольников Луч АВ – биссектриса

Q P В А М Докажем, что а РМ М a Построение перпендикулярных прямых.

Докажем, что а РМ АМ=МВ, как радиусы одной окружности. АР=РВ, как радиусы одной окружности АРВ р/б 3. РМ медиана в р/б треугольнике является также ВЫСОТОЙ. Значит, а РМ. М М a a В А Q P

a N М Построение перпендикулярных прямых. Докажем, что а MN М a

a N B М a A C 1 = 2 1 2 В р/б треугольнике АМВ отрезок МС является биссектрисой, а значит, и высотой. Тогда, а МN. М Докажем, что а MN Посмотрим на расположение циркулей. АМ=АN=MB=BN, как равные радиусы. МN-общая сторона. MВN= MAN, по трем сторонам

Докажем, что О – середина отрезка АВ. Q P В А О Построение середины отрезка

Q P В А АРQ = BPQ, по трем сторонам. 1 2 1 = 2 Треугольник АРВ р/б. Отрезок РО является биссектрисой, а значит, и медианой. Тогда, точка О – середина АВ. О Докажем, что О – середина отрезка АВ.

D С Построение треугольника по двум сторонам и углу между ними. Угол hk h Построим луч а. Отложим отрезок АВ, равный P1Q1. Построим угол, равный данному. Отложим отрезок АС, равный P2Q2. В А Треугольник АВС искомый. Обоснуй, используя I признак. Дано: Отрезки Р1Q1 и Р2Q2 Q1 P1 P2 Q2 а k

D С Построение треугольника по стороне и двум прилежащим к ней углам. Угол h1k1 h2 Построим луч а. Отложим отрезок АВ, равный P1Q1. Построим угол, равный данному h1k1. Построим угол, равный h2k2 . В А Треугольник АВС искомый. Обоснуй, используя II признак. Дано: Отрезок Р1Q1 Q1 P1 а k2 h1 k1 N

С Построим луч а. Отложим отрезок АВ, равный P1Q1. Построим дугу с центром в т. А и радиусом Р2Q2. Построим дугу с центром в т.В и радиусом P3Q3. В А Треугольник АВС искомый. Обоснуй, используя III признак. Дано: отрезки Р1Q1, Р2Q2, P3Q3. Q1 P1 P3 Q2 а P2 Q3 Построение треугольника по трем сторонам.