Тема уроку. Поняття об'єму. Основні властивості об'ємів. Об'єм прямокутного паралелепіпеда.

Мета уроку: формування поняття об'єму; вивчення основних властивостей

об'ємів; виведення формули для об'єму прямокутного паралелепіпеда; формування вмінь знаходити об'єм прямокутного паралелепіпеда.

Обладнання: моделі прямокутного паралелепіпеда.

І. Перевірка домашнього завдання

Наприкінці уроку збираються учнівські зошити для перевірки вико­нання домашнього завдання та ведення зошитів.

II. Сприйняття та усвідомлення нового матеріалу

Об'єм, основні властивості об'ємів

Кожне геометричне тіло займає частину простору.

Об'ємом геометричного тіла будемо називати додатне число, яке характеризує частину простору, що займає геометричне тіло, і за­довольняє таким умовам:

1. Рівні тіла мають рівні об'єми.

2. Якщо тіло розбите на кілька частин, то його об'єм дорівнює сумі об'ємів усіх цих частин.

3. Об'єм куба, ребро якого дорівнює одиниці довжини, дорівнює одиниці.

Куб, довжина ребра якого дорівнює одиниці довжини, називають одиничним.

Об'єм одиничного куба приймають за одиницю об'єму, називаючи таку одиницю кубічною.

Наприклад: кубічний сантиметр — це об'єм куба, ребро якого дорів­нює 1 см.

Виконання вправ

Поясніть, що таке:

а) 1 кубічний кілометр;

б) 1 кубічний метр;

в) 1 кубічний дециметр;

г) 1 кубічний міліметр.

Одиниці об'єму записують скорочено:

1 кубічний кілометр = 1 куб. км = 1 км³;

1 кубічний метр = 1 куб. м = 1 м³;

1 кубічний сантиметр = 1 куб. см = 1 см³;

1 кубічний дециметр = 1 куб. дм = 1 дм³;

1 кубічний міліметр = 1 куб. мм = 1 мм³.

Одиниця об'єму 1 дм³ має й іншу назву — 1 літр. Співвідношення між цими величинами подано нижче:

  1 км³ = (10³)³ м³.

Виміряти об'єм, геометричного тіла — значить знайти число, яке показує, скільки одиничних кубів міститься в даному тілі.

На рис. показано тіла, складені з кубів із ребром 1 см, їх об'єми дорівнюють по 6 см³.

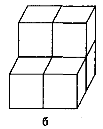
Тіла, які мають рівні об'єми, називаються рівновеликими.

Ми будемо далі розглядати лише прості тіла — тіла, які можна розбити на скінчене число трикутних пірамід. Вивчені многогранники: призми, піраміди, зрізані піраміди — є простими тілами.

Слід зазначити, що в «Началах» Евкліда і у творах Архімеда були виведені точні формули для знаходження об'ємів многогранників і де­яких тіл обертання (циліндра, конуса, кулі та їх частин).

К. Ж. Жордан (1838—1922) — французький математик, один із засновників сучасної математики, розробив в 1892 році теорію площ і об'ємів.

У минулому одиницями вимірювання об'єму були міри посудин, які використовувались для зберігання сипких і рідких тіл. Наприклад, в Англії: 36,4 дм³ — бушель; 4,5 дм³ — галон; 159 дм³ — барель; від 470 см³ до 568 см³ — пінта; на Русі: 12 дм³ — відро; 1,2 дм³ — штоф; 490 дм³ — діжка.

У давнину міра маси, а отже і об'єму, часто збігалась із мірою вартості товару — грошовою одиницею.

На Русі основна одиниця маси — гривня — була водночас грошовою одиницею. Гривня — злиток срібла, маса якого наближено дорівнювала 1 фунту - 96 золотникам, 1 золотник -4,3 г.

У другій половині XIII ст. гривню почали рубати пополам і назвали рублем, який із XV ст. став основною грошовою одиницею.

Зараз в Україні гривня — грошова одиниця.

Формула для об'єму прямокутного паралелепіпеда

Теорема

Об'єм прямокутного паралелепіпеда дорівнює добутку трьох його вимірів, тобто якщо a, b, c — лінійні виміри прямокутного паралелепі­педа, то його об'єм V обчислюється за формулою V = abc .

Доведення

Розглянемо три випадки.

1. Нехай виміри а, b, с прямокутного паралелепіпеда виражені натуральни­ми числами. Такий паралелепіпед мо­жна розрізати на с шарів, кожний з яких містить ab одиничних кубів. Отже, об'єм цього парале­лепіпеда:

V = аbс.

2. Нехай виміри а, b, с прямокутного паралелепіпеда виражені раціо­нальними числами. Зведемо ці числа до спільного знаменника, одержимо: , , , де т, п, р, q — натуральні числа.

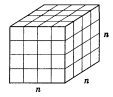Розіб'ємо паралелепіпед на куби, довжина ребра яких дорівнює частини одиниці довжини, загальна кількість таких кубів до­рівнює mpq. Згідно з властивістю об'ємів об'єм паралелепіпеда дорівнює добутку об'єму одного із цих кубів на число mpq. Але об'єм куба з ребром одиниці довжини дорівнює частини об'єму одиничного куба. Отже,

ІІІ. Розв'язування задач

1. Знайдіть об'єм куба, ребро якого дорівнює 5 см. (Відповідь. 125 см³.)

2. Знайдіть об'єм куба, якщо площа повної поверхні дорівнює 150 см². (Відповідь. 125 см³.)

3. Об'єм куба дорівнює 8 см³. Знайдіть площу повної поверхні куба.

(Відповідь. 24 см².)

4. Знайдіть об'єм куба, діагональ якого дорівнює d. (Відповідь. )

5. Знайдіть об'єм куба, площа грані якого дорівнює Q. (Відповідь. .)

6. Знайдіть об'єм куба, діагональ грані якого дорівнює d. (Відповідь. .)

7. Площі граней прямокутного паралелепіпеда дорівнюють S₁, S₂, S₃. Доведіть, що V = .

Розв'язання

Якщо виміри паралелепіпеда а, b, с, то ab = S₁, ас = S₂, bc = S₃.  Перемноживши ці рівності, маємо: a²b²c² = S₁S₂S₃.

Тоді об'єм паралеле­піпеда 

 V = аbс = .

8. Знайдіть об'єм піраміди, основа якої — грань куба, що має об'єм V, а вершина піраміди — точка перетину діагоналей цього куба. (Відповідь. .)

IV. Підведення підсумку уроку

Запитання до класу

1) Сформулюйте основні властивості об'єму.

2) Що таке 1 см³; 1 м³; 1 мм³; 1 дм³; 1 км³?

3) Чому дорівнює об'єм прямокутного паралелепіпеда?

4) Знайдіть об'єм прямокутного паралелепіпеда, якщо його виміри до­рівнюють 6 см, 9 см, 7 см. (Відповідь. 378 см³.)

5) У кубі, об'єм якого V, знаходиться правильний октаедр так, що всі його шість вершин збігаються з центрами граней куба. Знайдіть V об'єм октаедра. (Відповідь. .)

V. Домашнє завдання

____________________________________________________________________