Тема уроку.  Об'єм призми.

Мета уроку: засвоєння  формули для об'єму призми; формування умінь знаходити об'єм призми.

Обладнання: моделі призм.

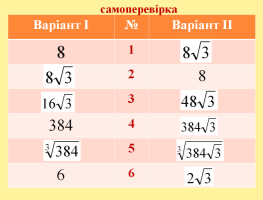
І. Перевірка домашнього завдання

Перевірити правильність виконання домашніх задач

ІI. Сприйняття та усвідомлення нового матеріалу

Доведення теореми про об'єм призми

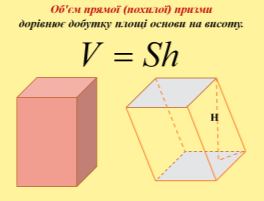
ІІІ. Розв'язування задач

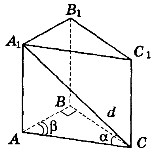
Задача 1 (для індивідуальної роботи). В основі прямого паралелепіпеда лежить ромб із більшою діагонал­лю d. Більша діагональ паралелепіпеда утворює з площиною осно­ви кут β, а менша — кут α. Знайдіть об'єм паралелепіпеда.

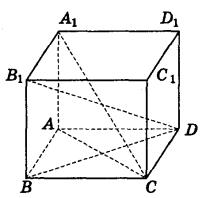Розв'язання

Нехай ABCDA₁B₁C₁D₁ — паралелепіпед, АА₁ (АВС) , ABCD — ромб, BD > AC , BD = d .

Ортогональними проекціями діагоналей А₁С і B₁D на площину ос­нови є відповідно діагоналі АС і BD ромба. Оскільки в прямокутних трикутниках АА₁С (<A = 90°) і B₁BD (<B = 90°) катети А₁А і В₁В рівні, а BD > АС , то діагональ В₁D більша, а А₁С — менша. Отже, <B₁DB = β, <A₁CA = α.

V = SH.

Із ΔВ₁ВD  BB₁ = H = BD tg <D = d tg β.

Із ΔА₁АС  AC = AA₁ ctg <C = H ctg α = d tg β ctg α .

Тоді S = BD · AC = d · d tg β ctg α = d² ctg α tg β.

V = d² ctg α tg β · d tg β = d³ ctgα tg²β.

Відповідь. d³ ctgα tg²β.

Задача 2 (для індивідуальної роботи).  Основа прямого паралелепіпеда — ромб зі стороною а, кут між пло­щинами двох суміжних бічних граней дорівнює φ (φ < 90°), біль­ша діагональ паралелепіпеда утворює з площиною основи кут β. Знайдіть об'єм паралелепіпеда. (Відповідь. 2a³ sin φ cos tg β.)

Колективне розв'язування задач

Задача №1. В основі прямої призми лежить прямокутний трикутник із катета­ми 6 і 8 см. Висота призми дорівнює 10 см. Знайдіть об'єм призми. (Відповідь. 240 см³.)

Задача №2. В основі прямої призми лежить трикутник, сторона якого дорівнює 12 см, а висота, проведена до неї — 5 см. Бічне ребро призми дорів­нює 8 см. Знайдіть об'єм призми. (Відповідь. 240 см³.)

Задача №3. В основі прямої призми лежить рівнобедрений трикутник, основа якого дорівнює 12 см, а висота, проведена до неї — 8 см. Знайдіть об'єм призми, якщо її висота дорівнює 10 см. (Відповідь. 480 см³.)

Задача №4. В основі прямої призми лежить трапеція з основами 9 і 15 см і ви­сотою 5 см. Знайдіть об'єм призми, якщо її бічне ребро дорівнює 10 см.

(Відповідь. 600 см³.)

Задача №5. Сторона основи правильної чотирикутної призми дорівнює 5 см, а діагональ бічної грані — 13 см. Знайдіть об'єм призми. (Відпо­відь. 300 см³.)

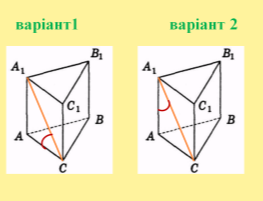
Задача №6.  Основою прямої призми є рівнобедрений трикутник з основою 16см і бічною стороною 17см. Діагональ бічної грані, що містить основу цього трикутника, утворює з площиною основи призми кут 30˚. Знайдіть об’єм призми.

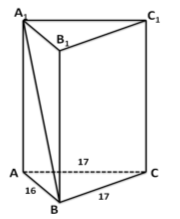
Розв’язання

∆BAA₁:  

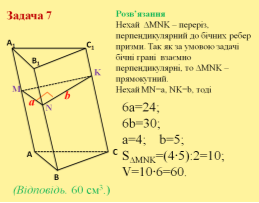
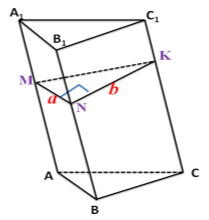
Задача №7.  Бічне ребро похилої трикутної призми дорівнює 6 см, дві бічні гра­ні її взаємно перпендикулярні і мають площі 24 см² і 30 см². Знай­діть об'єм призми. (Відповідь. 60 см³.)

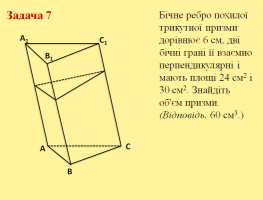
Розв’язання

Нехай  ∆MNK – переріз, перпендикулярний до бічних ребер призми. Так як за умовою задачі бічні гра­ні  взаємно перпендикулярні, то ∆MNK – прямокутний. Нехай MN=a, NK=b,тоді

6a=24;

6b=30;

a=4;

b=5;

S_∆MNK=(4·5):2=10;

V=10·6=60.

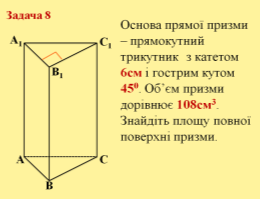
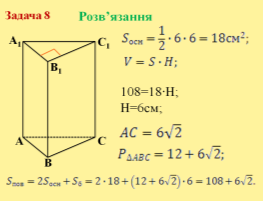
Задача №8. Основа прямої призми – прямокутний трикутник  з катетом 6см і гострим кутом 45⁰. Об’єм призми дорівнює 108см³. Знайдіть площу повної поверхні призми.

Розв’язання

108=18·H;

H=6см;

Задача №9.

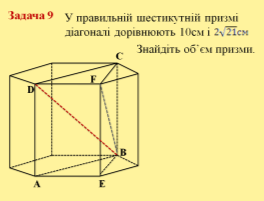
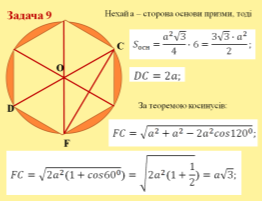
Нехай дано правильну шестикутну призму,  діагоналі DB=10см і FB=2√21см. Знайдемо  об’єм призми: 

Нехай a – сторона основи призми, тоді

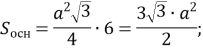
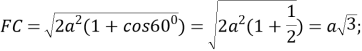
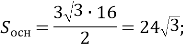
IV. Підведення підсумку уроку

Запитання до класу

Чому дорівнює об'єм довільної призми?

Запишіть формулу для знаходження об'єму призми.

Чому дорівнює об'єм похилої призми?

В основі прямої призми лежить прямо­кутний трикутник із гострим кутом р .  Діагональ бічної грані, яка міс­тить гіпотенузу, дорівнює а і утворює з площиною основи кут α. Укажіть, які з наведених тверджень правильні, а які — неправильні:

а) висота призми дорівнює d cos α;

б) гіпотенуза основи дорівнює d cos α;

в) катет, прилеглий до кута β, дорівнює d sin α cos β;

г) площа основи дорівнює d² cos² α sin 2β;

д) об'єм призми дорівнює d³ cos² α sin α sin 2β.

V. Домашнє завдання

________________________________________________________________________________________________________________________________________________________________________________________________________