Заняття з дистанційного курсу. "Множення десяткових дробів"

Заняття №5

Тема:  Множення десяткових дробів.

Цілі: cформувати  поняття та правило множення десяткових дробів; домогтися засвоєння переставної і сполучної властивостей множення десяткових дробів; розвивати  логічне мислення, математичні здібності, обчислювальні навички;   виховувати  культуру математичних записів та мови, уміння аналізувати і робити висновки, кмітливість, увагу;

виховувати любов до рідного міста.

    Алгоритм роботи:

1. Знайомство з теоретичним матеріалом, таблицею та презентацією.

2. Виконання практичних вправ репродуктивного, конструктивного та творчого характеру.

3. Повторення правил.

4. Перевірка знань, умінь та навичок (тестова робота).

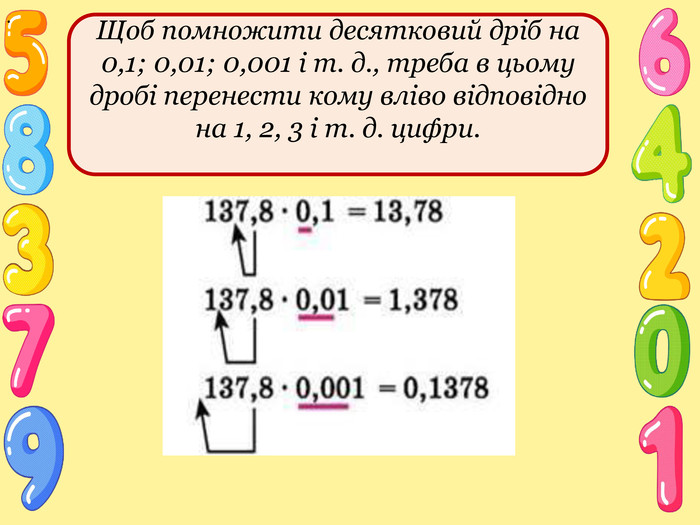
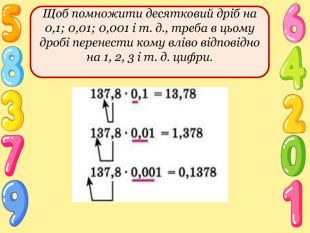
Матеріал для засвоєння.

Отже, якщо кому перенести вправо на 1, 2, 3 і т. д. цифри, то дріб збільшиться відповідно в 10, 100, 1000 і т. д. разів.

Якщо в добутку буде менше цифр, ніж потрібно відокремити комою, то попереду дописують потрібну кількість нулів.

Наприклад 1. Обчисліть зручним способом: 0,2 · 32,8 · 5 = 1 · 32,8 = 32,8.

Наприклад 2. Спростіть вираз: 0,6а · 0,8b.

0,6а · 0,8b = (0,6 · 0,8) · (ab) = 0,48аb.

Наприклад 3. Обчисліть значення виразу найзручнішим способом:

3,18 · 7,8 + 3,18 · 22 = 3,18(7,8 + 2,2) = 3,18 · 10 = 31,8.

Наприклад 4. Спростіть вираз і обчисліть його значення: 0,13р + 0,47р, якщо р = 0,14.

0,13р + 0,47р = 0,6p, якщо р = 0,14, то 0,6p = 0,6 · 0,14 = 0,084.

Практичні завдання.

1. Виконайте дії:

1) 2,53 · 10; 2) 2,53 · 100; 3) 2,53 · 1000.

2. Виконайте дії:

1)4,6 · 0,1;  2)4,6 · 0,01;  3)4,6 · 0,001.

3. Знайдіть пропущені числа:

1) 35,1 · □ = 0,351; 2) 436 · □ = 0,436; 3) 6,58 · □ = 0,658; 4) 65,8 · □ = 6,58.

4. Використовуючи правило множення десяткових дробів, знайдіть до­буток:

1)4,6 і 0,8;  2)40,6 і 0,08;  3)0,46 і 0,008.

5. Сторони прямокутника мають довжину 5,07м і 3,2 м. Знайдіть площу цього прямокутника.

6. Обчислити:

1) 0,2 · 3 · 0,5; 2) 0,2 · 0,3 + 0,2 · 0,7;

7.Спростити:

1) 0,2а · 0,5b; 2) 0,2а + 0,5b.

Хвилинка ерудита.

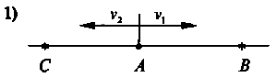
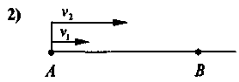
Два велосипедисти рухаються зі швидкістю v₁ і v₂.

1.                   вони виїхали з одного міста в протилежних напрямках (див. (1));

v_{віддалення} = v₁ + v₂

2) вони виїхали з одного міста в одному напрямку (рис. (2));

v = v₂ – v₁ (v₂ > v₁).

2.                   вони виїхали з двох міст назустріч один одному (рис. (3));

v_{зближення} = v₁ + v₂

3.                   вони виїхали з двох міст в одному на­прямку, (рис. (4))
4.                   v = v₂ – v₁ (v₂ > v₁).

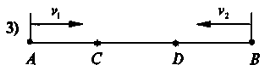
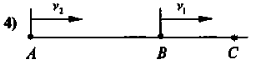
8. Задача. Два автомобілі з Харкова та Києва одночасно виїхали назустріч один одному. Швидкість одно з них в 1.5 раз більша, ніж швидкість другого. Вони зустрілись через 3 години. Знайдіть відстань між Харковом і Києвом, якщо середня швидкість першого 95,94 км/год.

Перевір себе!

• Як помножити десятковий дріб на 10? на 100? на 1000?
• Як помножити два десяткових дроби?
• Як помножити десятковий дріб на 0,1? на 0,01? на 0,001?
•  Які властивості множення натуральних чисел виконуютьсяі для дробових чисел?

Тестові завдання

Завдання 1- 6 мають по 4 варіанти відповіді,

серед яких 1 правильний (за кожне 1 б.)

1.                   Укажіть букву, що відповідає правильній відповіді.

Скільки десяткових знаків потрібно відокремити комою в добутку 4,5·3,44?

А. Один;

Б. Два;

В. Три;

Г. Чотири.

2.  Виконайте множення 2,43·6.

А.14,58;

Б.145,8;

В.14,68;

Г.1,485.

3. Який з наведених добутків дорівнює 8?

А.0,032·2500;

Б.3,2·2,5;

В.0,32·250;

Г.320·0,25.

4. Який з наведених добутків найменший?

А.1,1·4,3;

Б. 28·0,17;

В.0,25·19;

Г.0,6·0,9

5. Коренем рівняння  х : 4,2= 12,6 є число:

А.3;

Б.52,92;

В. 0,03;

Г.520,8.

6. При якому з наведених х значення виразу 0,128·1,002х найбільше?

А. 0,9;

Б.0,5;

В. 0,008;

Г.1,001.

У завданні 7-8 необхідно указати відповідь.

(кожне завдання — 1 б.)

7. Скільки кілометрів подолає потяг зі швидкістю 75 км/год за 4,8 год?

Відповідь: __________________

8. Знайдіть значення виразу:

 0,25·34,986·0,4·10 

Відповідь: __________________

Завдання 11-12 — встановлення відповідності між рядками. До кожного рядка, позначеного цифрою, доберіть відповідник, позначений буквою. (кожне завдання — 2 бали).

11. Установіть відповідність між виразом та його значенням.

12. Установіть відповідність між виразом та його значенням.