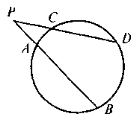Застосування подібності: властивість бісектриси трикутника
Тема. Застосування подібності: властивість бісектриси трикутника
Мета: домогтися засвоєння учнями змісту теореми, що виражає властивість бісектриси трикутника та її доведення. Формувати вміння:
- відтворювати зміст вивченої теореми;
- за готовими рисунками із зображенням трикутника та його бісектриси знаходити пропорційні відрізки;
-
виконувати записи відповідно до формулювання теореми та умови
задачі; -
застосовувати формулювання теореми до розв’язування задач на
обчислення відрізків у трикутнику.
Тип уроку: застосування знань, умінь та навичок.
Наочність та обладнання: конспект «Застосування подібності трикутників».
Хід уроку
I. Організаційний етап
II. Перевірка домашнього завдання
За необхідності перевірити виконання письмової частини домашнього завдання проводиться усна робота за готовими рисунками до домашніх задач.
Засвоєння змісту матеріалу попереднього уроку та формування оперативних умінь можна перевірити під час виконання учнями тестового завдання.
Тестове завдання
-
Яке з тверджень не є наслідком теореми Піфагора? Якщо з однієї
точки до прямої проведено перпендикуляр і похилі, то:
1) похилі більші від перпендикуляра;
2) рівні похилі мають рівні проекції;
3) з двох похилих більша та, у якої проекція більша;
4) перпендикуляр більший за проекцію похилої.
- З точки М опущено перпендикуляр MN = 12 см на пряму а і проведено похилі MP = 13 см і MQ = 15 см. Знайдіть різницю між проекціями цих похилих.
1) 5см; 2) 9 см; 3) 4 см; 4) 3 см..
- Пожежну драбину, довжина якого 25 м, приставлено до даху будинку. Проекція драбини на землю дорівнює 15 м. Яка висота стіни будинку?
1) 18 м; 2) 19 м; 3) 20 м; 4)21 м.
- Нехай MN — перпендикуляр, опушений з точки М на пряму а; MP, MQ, MR — похилі, проведені з точки основи перпендикуляра N відповідно на 18, 15 і 14 см. Яка з похилих має найбільшу довжину?
1) MR; 2) MQ; 3) MP.
- З точки М до прямої проведено перпендикуляр довжиною і 2 см і дві похилі, одна з яких утворює із своєю проекцією кут 45°, а друга дорівнює 13 см. Яка довжина суми проекцій?
1) 7 см; 2) 18 см; 3) 17 см; 4) 16 см.
III. Формулювання мети і завдань уроку
Учитель нагадує учням (або організує роботу таким чином, щоб учні самі «проговорили»), що всі твердження про прямокутний трикутник, які були вивчені протягом останніх трьох уроків, ґрунтуються на застосуванні до прямокутного трикутника метричних співвідношень, що випливають із подібності прямокутних трикутників.
Проте доведеними властивостями для прямокутного трикутника практичне значення подібності трикутників не обмежується. Новий матеріал, вивчення якого починається на цьому уроці, вміщує деякі зі співвідношень відрізків у трикутнику та в колі, які є результатом застосування подібності трикутників. Отже, мета уроку — вивчення одного з таких співвідношень (під вивченням, звісно, слід розуміти ознайомлення зі змістом, доведення, опанування способами практичного застосування).
IV. Актуалізація опорних знань
З метою успішного засвоєння учнями змісту навчального матеріалу уроку учням слід активізувати знання і вміння щодо поняття пропорційних відрізків; означення подібних трикутників та ознаки подібності прямокутних трикутників за гострим кутом; означення бісектриси трикутника.
Виконання усних вправ
-
Дано:
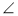 1 =
1 = 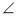 2 (рис. 1). Доведіть, що
2 (рис. 1). Доведіть, що 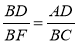 .
.
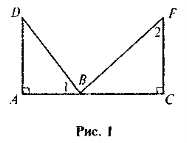
-
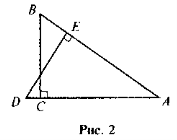
ΔАВС і ΔADE — прямокутні і рівні (рис. 2). Доведіть, що
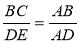 .
.
- ΔАВМ ~ ΔВ1А1С1, В, М, А, Н — висоти (рис. 3). Доведіть, що
ΔАВМ ~ Δ А1В1Н1.
-
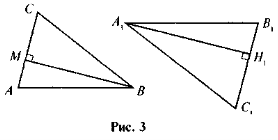
ΔАВМ ~ΔА1ВC, ABCD — паралелограм, ВМ
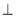 AD, BH
AD, BH 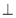 CD (рис. 4). Доведіть, що
CD (рис. 4). Доведіть, що 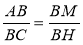 .
.
- Визначте, чи є відрізки завдовжки а і b пропорційними відрізкам с і d, якщо:
а) a = 8 см; b = 24 см; c = 4 см; d = 12 см;
б) а = 9 см, b = 14 см; c = 7 см, d = 18 см.
V. Засвоєння знань
План вивчення нового матеріалу
- Теорема про властивість бісектриси трикутника: формулювання і доведення.
- Приклади застосування властивості бісектриси трикутника.
Властивість бісектриси трикутника традиційно вивчається у зв'язку з подібністю прямокутних трикутників (див. Геометрія, 7-9, О.В.Погорєлов, п.106). Зміст і спосіб доведення відповідної властивості в новому підручнику, порівняно з традиційним, не змінено; відмінність полягає тільки в тому, що властивість бісектриси трикутника подано як теорему, а тому вміння відтворювати та застосовувати зміст цієї властивості є однією з програмових вимог.
|
Конспект 15 |
|
|
Застосування подібності трикутників |
|
|
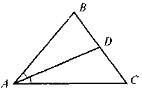
Властивість бісектриси трикутника
Якщо в ΔАВС: D Бісектриса трикутника ділить протилежну сторону на відрізки, пропорційні двом іншим сторонам. |
|
|
Метричні співвідношення в колі |
|
|
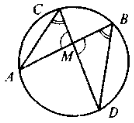
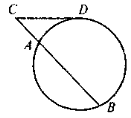
1) Якщо АВ і CD — хорди кола (0; r), М — точка їх перетину, то AM · MB = CM · MD. 2) Якщо СВ — січна, CD — дотична до кола (0; r) ( D — точка дотику); СА — зовнішня частина січної, то CD2 = CB · CA. |
|
|
|
|
|
Наслідок. Якщо PD і РВ — січні до кола, PC і РА — їх зовнішні частини, то РА · РВ = PC · PD |
|
VІ. Формування первинних умінь
Виконання усних вправ
- Точки М і Р — середини суміжних сторін AD і DC паралелограма ABCD відповідно. Відрізки МС і РВ перетинаються в точні К . Знайдіть відношення ВК : КР.
- Чи може бісектриса рівнобедреного трикутника ділити бічну сторону у відношенні 2:1, починаючи від основи? Якій теоремі це суперечить?
- Накресліть трикутник ABC і проведіть його бісектрису BD. Виміряйте відрізки АВ , AD і DC . За допомогою властивості бісектриси трикутника обчисліть довжину сторони ВС . Перевірте результат вимірюванням.
Виконання графічних вправ
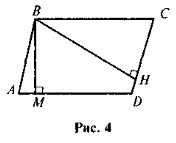
- Побудуйте трикутник ABC зі сторонами АВ = 6 см, ВС = 7 см. АС = 8 см. Позначте на стороні ВС точку D так, щоб BD = 3 см, Сполучіть точки А і D. Виміряйте кути BAD і CAD. Обґрунтуйте здобутий результат.
Виконання письмових вправ
- Відрізок BD — бісектриса трикутника ABC. Знайдіть АВ, якщо ВС = 8 см, AD = 3 см, DC = 2 см.
- Відрізок BD — бісектриса трикутника ABC. Знайдіть стороні! трикутника, якщо AD = 8 см, DC = 12 см, а периметр трикутника дорівнює 45 см.
- Бісектриса прямокутного трикутника ділить його катет на відрізки завдовжки 4 см і 5 см. Знайдіть периметр трикутника.
4*. Діагоналі рівнобічної трапеції є бісектрисами її гострих кутів. Знайдіть середню лінію трапеції, якщо її периметр дорівнює 22 см. а діагональ ділить висоту, проведену з вершини тупого кута, у відношенні 4 : 3.
Опрацювання матеріалу уроку розпочинається з виконання усних вправ на розуміння змісту теореми про властивість бісектриси трикутника (на готовому рисунку) та за описом ситуації (якщо необхідно, виконання вправ можна супроводжувати виконанням рисунків). Виконання графічних вправ сприяє формуванню в учнів математичної культури. Формування вмінь застосовувати властивість бісектриси трикутника відбувається під час виконання письмових вправ різного рівня складності — від вправ на пряме застосування теореми (у тому числі й задачі на складання рівнянь) до вправ на застосування теореми про властивість бісектриси трикутника в комплексі із знаннями, набутими на попередніх уроках (як у 7-му, так і 8-му класах). Задачі підвищеної складності передбачають вільне володіння всім об'ємом навчального матеріалу 8 класу.
VII. Підсумки уроку
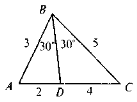
Які помилки допущено в зображенні трикутників?
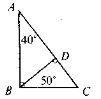
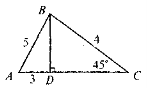
VIII. Домашнє завдання
Вивчити зміст теореми. Розв'язати задачі.
- Бісектриса рівнобедреного трикутника ділить бічну сторону на відрізки завдовжки 2 см і 4 см, починаючи від основи трикутника. Знайдіть основу трикутника.
- Бісектриса прямокутного трикутника ділить гіпотенузу на відрізки, різниця яких складає 5 см. Знайдіть сторони трикутника, якщо відношення катетів дорівнює 3 : 4.
- Бісектриса кута при основі рівнобедреного трикутника ділить висоту, проведену до основи, на відрізки завдовжки 16,5 см і 27,5 см. Знайдіть відрізки, на які ця бісектриса ділить бічну сторону трикутника.
Повторити теорему про вписані кути та її наслідки.


про публікацію авторської розробки
Додати розробку