Розв'язування задач на подібність трикутників

Тема. Розв'язування задач на подібність трикутників

Мета: узагальнити та систематизувати знання учнів про зміст та схеми застосування теорем, що випливають із подібності трикутників (властивості бісектриси трикутника та метричних співвідношень у колі); удосконалювати вміння та навички застосування набутих знань.

Тип уроку: застосування знань, умінь та навичок.

Наочність та обладнання: конспект 15.

Хід уроку

I. Організаційний етап

II. Перевірка домашнього завдання

Засвоєння учнями матеріалу поперед­нього уроку (метричні співвідношення в колі) можна провести у формі «німого» диктанту. На дошці виконане зображення ситуацій, що можуть бути описані метрич­ними співвідношеннями в колі (рис. 1).

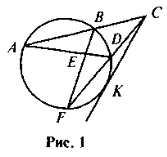
Учитель формулює загальне завдання для всіх учнів: для відрізків, на які він буде вказувати, записати пра­вильну рівність (відповідне метричне співвідношення). 1 далі мовчки вказує по черзі на відрізки хорд, січних, дотичних. По закінченні ви­конання роботи відбувається само- або взаємоперевірка робіт із комен­тарем.

III. Формулювання мети і завдань уроку

Якість виконання роботи на попередньому етапі уроку дає можливість учителю сформулювати мету уроку або як закріплення знань, набутих під час вивчення застосування подібності трикутників та продовження роботи із формування навичок практичного застосування знань, або ж як відпрацювання навичок застосування знань та вдосконалення вмінь.

IV. Закріплення знань учнів

Повторення та систематизація знань учнів про зміст тверджень, які випливають із подібності трикутників, можна провести в такій формі: до уваги учнів пропонується рис. 2, за яким вони виконують завдання: для кожного з рисунків скласти найбільш відповідне твердження (у математичному та словесному вигляді). Для того щоб залучити до роботи якомога більше учнів, можна організувати роботу в малих групах. У такому разі спочатку завдання виконується в групах, а потім результати презентуються та в разі необхідності коригуються.

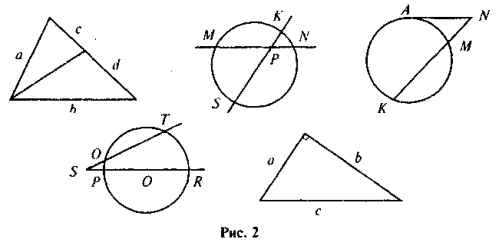
VI. Удосконалення вмінь

Застосування знань у стандартних ситуаціях

1. Бісектриса кута при основі рівнобедреного трикутника ділить ви­соту, проведену до основи, на відрізки завдовжки 16,5 см і 27,5 см. Знайдіть відрізки, на які ця бісектриса ділить бічну сторону три­кутника.
2. Відрізок ВР є бісектрисою трикутника ABC. Знайдіть:

а) АВ. якщо ВС = 9 см, АР = 7,5 см, PC = 4,5 см;

б) PC, якщо АВ = 30 см, АР = 20 см, ВР = 16 см і BPC = C;

в) РС, якщо АВ = 14 см, ВС = 20 см, АС = 21 см.

3. Хорди АВ і СК перетинаються в точці Р. Знайдіть довжини хорд, якщо відомо, що:

1) АР = 8 см, ВР = 12 см і СК : РК = 3 : 8;

2) АР : РВ = 16 : 1, СК – СР = 9 см і АВ + СК = 76 см.

Застосування знань у нестандартній ситуації

1. Катет прямокутного трикутника дорівнює 28 см. Точка, що нале­жить гіпотенузі, віддалена від кожного з катетів на 12 см. Знайдіть довжини відрізків, на які ця точка ділить гіпотенузу.
2. У трикутник MNK вписано ромб MDEF так, що вершини D, Е і F лежать відповідно на сторонах MN, NK і МК. Знайдіть відрізки NE і ЕК, якщо  MN = 7 см, NK = 6 см, МК = 5 см.

 Застосування знань у стандартних ситуаціях означає розв'язування задач, в яких запитання стосується певного співвідношення. Розв'язування таких задач допомагає учням сформувати навички про­ведення доказових міркувань із використанням вивчених тверджень.

Нестандартність ситуацій, описаних у задачах 1 і 2, полягає в тому, що ці задачі вимагають від учнів упевненого володіння матеріалом, вивченим як у 7-му, так і у 8-му класах (властивість діагоналей ромба, означення відстані від точки до прямої; властивість точок кола та властивість дотичної до кола, властивість вписаного кута, що спирається на діаметр), а також нестандартного мислення.

VII. Підсумки уроку

Закінчивши розв'язання задач, учні здійснюють самооцінку знань і вмінь та усвідомлюють, над якими питаннями теми слід додатково працювати.

VIІ. Домашнє завдання

Повторити зміст основних понять теми. Розв'язати задачі.

1. Відрізок BD — бісектриса трикутника ABC. Знайдіть:

а) АВ, якщо ВС = 8 см, AD = 3 см, DC = 2 см;

б) AD і DC, якщо АВ = 9 см, DC = 6 см, АС = 10 см.

2. Побудуйте трикутник за двома кутами і висотою, проведеною з вер­шини третього кута.

Самостійна робота на повторення

1. На рис. ІABCD— прямокутник. Знайдіть х.

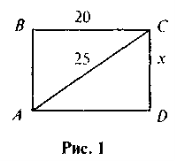
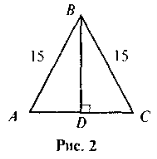
2. На рис. 2  АС = 18 . Знайдіть BD.
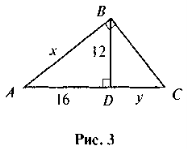
3. За даними рис. 3 знайдіть х і у.

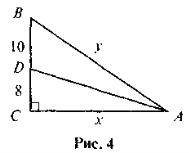
4. За даними рис. 4 знайдіть х і у.