Завдання для проведення самостійних робіт з геометрії (10 клас).
Завдання для проведення самостійних робіт розроблені з метою виявлення рівня навчальних досягнень учнів з двох основних тем з геометрії (10 клас, рівень стандарту), а саме:«Паралельність прямих і площин у просторі» та «Перпендикулярність прямих і площин у просторі».
Також запропоновані завдання дозволяють узагальнити і систематизувати знання учнів з названих тем, повторити основні способи геометричних задач.
Самостійні роботи з геометрії (10 клас).
Тема. Паралельність прямих і площин у просторі.
Варіант 1.
У завданнях 1-6 позначте правильну, на вашу думку, відповідь.
- Побудуйте зображення куба ABCDA1B1C1D1. Прямі AC і A1C1…
|
А. паралельні |
Б. перетинаються |
В. мимобіжні |
Г. не можна визначити |
- Якщо дві прямі a і b мають спільну точку C, то через них можна провести…
|
А. одну площину |
Б. |
В. |
Г. безліч площин |
-
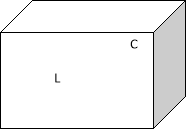
Дано зображення прямокутного паралелепіпеда ABCDKLMN. Якій площині належать пряма KL і точка N ? A B
D
N
LL
K M
|
А. (MKL) |
Б. (BNM) |
В. |
Г. (ACL) |
4. Прямі c і b паралельні. Як розміщена пряма b відносно площини α, якщо пряма c перетинає площину α .
|
А. належить площині |
Б. перетинає площину |
В. паралельна площині |
Г. не можна визначити |
5. Паралелограм ABMN і трикутник ABC не лежать в одній площині. K, L - середини сторін AC і BC відповідно. Доведіть, що CD||MN.
6. Дано трикутну піраміду SABC. Довести, що прямі SB і AC мимобіжні.
7. Площина α перетинає сторони АВ і АС трикутника АВС у точках В1 і С1 відповідно, причому АС1:С1С=3:2 і В1С1= 5 см. Знайдіть довжину відрізка ВС, якщо пряма ВС і площина α паралельні.
Варіант 2.
У завданнях 1-4 позначте правильну, на вашу думку, відповідь.
- Побудуйте зображення куба ABCDA1B1C1D1. Прямі BC і AA1…
|
А. паралельні |
Б. перетинаються |
В. мимобіжні |
Г. не можна визначити |
2. Дано пряму a і точку F, яка не лежить на ній. Через них можна провести…
|
А. одну площину |
Б. |
В. |
Г. безліч площин |
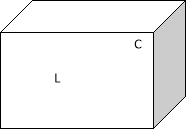
3.Дано зображення прямокутного паралелепіпеда ABCDKLMN. Якій площині належать пряма BN і точка C ? A B
D
N
K M
|
А. (ABN) |
Б. (KMN) |
В. (ABC) |
Г. (MNC) |
4. Прямі a і b паралельні. Пряма b належить площині α, а пряма a не належить площині α. Як розміщені пряма a і площина α ?
|
А. пряма належить площині |
Б. пряма перетинає площину |
В. пряма паралельна площині |
Г. не можна визначити |
5. Паралелограм ABCD і трапеція ABMN (AB – основа трапеції) не лежать в одній площині. Доведіть, що CD||MN.
6. Дано трикутну піраміду SABC. Довести, що прямі AS і BC мимобіжні.
7. Площина, паралельна стороні ВС трикутника АВС, перетинає сторони АВ і АС у точках В1 і С1 відповідно, причому АВ1:ВВ1=5:3. Знайдіть В1С1, якщо ВС=6 см.
Тема . Перпендикулярність прямих і площин у просторі.
Варіант 1.
Початковий і середній рівні
У завданнях 1-6 виберіть правильну, на вашу думку, відповідь.
- Похила завдовжки 12 м утворює з площиною кут 300 .Знайдіть довжину проекції цієї похилої на площину.
|
А |
Б |
В |
Г |
|
6 м |
6 |
24 м |
12 |
-
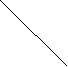
Дано квадрат ABCD; SO (ABC); OF CD ( рис. 2). Довжина якого із зазначених відрізків є відстанню від точки S до прямої CD ?
|
А |
Б |
В |
Г |
|
SD |
SF |
SC |
SO |
S
B C
F
A
D
- Двогранний кут дорівнює 450 . На одній із його граней дано точку, розташовану на відстані 6 см від другої грані. Знайдіть відстань від цієї точки до ребра двогранного кута.
|
А |
Б |
В |
Г |
|
6 |
|
6 см |
3 см |
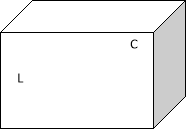
- Дано зображення прямокутного паралелепіпеда ABCDLNMK. Встановити відповідність між твердженням(1-4) і прямою (А-Г) :
A B
D
D
N
K
K M
|
А. MN |
|
Б. AВ |
|
В. MB |
|
Г. AD |
5. Яка з наведених фігур може бути паралельною проекцією трапеції ?
|
А |
Б |
В |
Г |
|
ромб |
паралелограм |
трапеція |
рівнобедрений трикутник |
6. Площа ортогональної проекції многокутника відноситься до площі цього многокутника як 
: 2. Чому дорівнює кут між їх площинами ?
|
А |
Б |
В |
Г |
|
900 |
600 |
450 |
300 |
Достатній рівень
7. Дано куб ABCDA1B1C1D1. Довести, що площина (АВ1С) паралельна площині (А 1С1 D) .
8. Площини α і β паралельні між собою і перетинають сторону АО кута АОВ у точках С і С1, а сторону ОВ – у точках D і D1 відповідно. Обчисліть довжину відрізка CD, якщо C1D1= 9 см, CC1=14 см, ОС= 4 см.
Високий рівень
- Зобразіть куб ABCDA1B1C1D1. Побудуйте спільний перпендикуляр до прямих АА1 і СС1. Знайти:
- відстань між прямими АА1 і СС1, якщо ребро куба дорівнює 2 см;
- кут між площинами ( АА1D1) і (B D1D).
Варіант 2.
Початковий і середній рівні
У завданнях 1-6 виберіть правильну, на вашу думку, відповідь.
-
Похила AB завдовжки
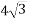см утворює з площиною кут 600 .Знайдіть АО – відстань від кінця похилої до площини.
|
А |
Б |
В |
Г |
|
8 см |
6 см |
|
|
-
До площини правильного трикутника АВС проведено перпендикуляр SA, AK BC. Довжина якого із зазначених відрізків є відстанню від точки S до прямої ВC ?
|
А |
Б |
В |
Г |
|
SC |
SK |
SB |
SA |
S
C
A K
B
- Точка, яка лежить на одній із граней двогранного кута, розташована на відстані 7 см від другої грані. Знайдіть величину двогранного кута, якщо відстань від точки до ребра двогранного кута 14 см.
|
А |
Б |
В |
Г |
|
900 |
450 |
600 |
300 |
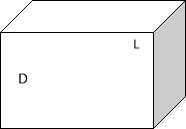
- Дано зображення прямокутного паралелепіпеда ABCDKLMN. Встановити відповідність між твердженням (1-4) і прямою (А-Г) :
N M
K
D DD С
А
В
|
А. ВN |
|
Б. KM |
|
В. DN |
|
Г. AD |
5. Яка з наведених фігур не може бути паралельною проекцією прямокутника?
|
А |
Б |
В |
Г |
|
паралелограм |
трапеція |
прямокутник |
квадрат |
6. Площа многокутника відноситься до площі його ортогональної проекції як 2 : 1. Чому дорівнює кут між їх площинами ?
|
А |
Б |
В |
Г |
|
900 |
600 |
450 |
300 |
Достатній рівень
- Дано куб ABCDA1B1C1D1. Довести, що площина (ВС1D) паралельна площині (АВ1 D1) .
- Площина α перетинає сторону АВ трикутника АВС у точці М, а сторону АС – у точці Р і паралельна стороні ВС. Знайдіть довжину сторони ВС, якщо АМ = 6 см, ВМ = 9 см, М Р = 4см.
Високий рівень
- Зобразіть куб ABCDA1B1C1D1. Побудуйте спільний перпендикуляр до прямих А1 B1 і СD. Знайти:
- відстань між прямими А1 B1 і СD, якщо ребро куба дорівнює 3 см;
- кут між площинами ( СС1D1) і (А1B1D).
про публікацію авторської розробки
Додати розробку