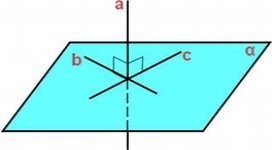
Розробка уроку геометрії на тему "Перпендикулярність прямої і площини".

	Розробка уроку геометрії на тему «ПЕРПЕНДИКУЛЯРНІСТЬ ПРЯМОЇ І ПЛОЩИНИ» викладач Токар С.М.   « Математика цікава тоді,                                             коли дає поживу нашій                                    винахідливості й                                                 здатності до міркувань.» Д. Пойа     Мета уроку: узагальнити і систематизувати навчальний матеріал про перпендикулярність прямої і площини; повторити основні типи задач і способи їх розв’язування; показати прикладне застосування геометрії, провести діагностику і корекцію рівня навченості ; розвивати просторову уяву й логічне мислення, пам’ять, увагу, уміння чітко й математично грамотно висловлювати свою думку;  виховувати ініціативність, самостійність, працьовитість, культуру спілкування під час роботи в малих групах. Методична мета: застосування методів узагальнення і систематизації навчального матеріалу; освітніх технологій, що сприяють активізації пізнавальної діяльності учнів ( робота в малих групах, інтерактивна технологія «Мозковий штурм», вправи «Геометричне лото», «Графічний диктант»). Тип уроку: узагальнення і систематизація знань,        умінь і навичок. Обладнання уроку: моделі «Перпендикуляр і похила», «Теорема про три перпендикуляри», роздавальний матеріал ( задачі з пропусками, креслення до задач, картки для «Геометричного лото», фішки).    ХІД УРОКУ. І. Організаційний етап. Група поділена на 4 команди.   ІІ. Повідомлення теми і мети уроку. Мотивація навчальної діяльності учнів. Вступне слово учителя. Необхідність перевіряти перпендикулярність прямої і площини на практиці виникає досить часто (під час будівництва об’єктів, установлення антен, вертикальних стовпів тощо). Заводські димові труби, телевізійні вежі, стовпи, нафтові свердловини і шахтні стволи, колодязі роблять перпендикулярними до площини горизонту. Голка швейної машини, свердло в свердлильному верстаті переміщують по прямій, перпендикулярній до площини станини. Бурильні установки, підйомні крани під час роботи встановлюють перпендикулярно до площини кріплення. Перпендикулярно до площини горизонту запускають космічні кораблі (згодом ракета – носій лягає на курс). Зважаючи на важливість вивчення цієї теми для розв’язування прикладних задач, узагальнимо основні теоретичні знання, повторимо основні типи задач з даної теми та способи їх  розв’язування. Наприкінці уроку проведемо діагностику рівня набутих знань, умінь і навичок.   ІІІ. Узагальнення і систематизація знань.   Робота в малих групах. Інтерактивна вправа «Геометричне лото».   ( Кожна команда отримує комплект карток. На одних є початок, на інших –продовження або закінчення твердження. Необхідно підібрати пари відповідних карток).       Роздавальний матеріал для проведення гри «Геометричне лото». (Знайдіть відповідність між частинами тверджень.)
1	Дві прямі називаються перпендикулярними,
І	якщо вони перетинаються під прямим кутом.
2	Ознака. Якщо 2 прямі, які перетинаються,
ІІ	паралельні відповідно 2 перпендикулярним прямим, то вони теж перпендикулярні.
3	Пряма називається перпендикулярною до площини, якщо вона перетинає цю площину
ІІІ	та перпендикулярна до будь-якої прямої, що лежить у цій площині й проходить через точку перетину.
4	Ознака. Якщо пряма перпендикулярна до 2 прямих,
ІV	які лежать у площині й перетинаються, то вона перпендикулярна до даної площини.
5	Перпендикуляром, опущеним з даної точки на дану площину, називають відрізок
V	прямої,перпендикулярної до площини, що міститься між даною точкою і площиною.
6	Проекцією похилої називається відрізок,
VI	що з’єднує основи перпендикуляра і похилої, проведених з однієї і тієї самої точки.
7	Якщо похилі, проведені до площини з 1 точки рівні, то
VII	рівні і їх проекції.
8	Перпендикуляр завжди
VIII	менше похилої, проведеної до площини з тієї ж точки.
VIII	більше похилої, проведеної до площини з тієї ж точки.
9	З двох похилих, проведених до площини з 1 точки, більшою є та,
IX	проекція якої більше.
IX	проекція якої менше.
10	Теорема про 3 перпендикуляри. Якщо пряма, що лежить в площині і проходить через основу похилої,
X	перпендикулярна до проекції похилої, то вона
XI	перпендикулярна і до самої похилої.
X	перпендикулярна до похилої, то вона
XI	перпендикулярна і до проекції похилої.

VІ. Узагальнення і систематизація вмінь та навичок.

Інтерактивна технологія «Мозковий штурм».

Учні кожної малої групи  заповнюють пропуски в розв’язуванні задачі, після чого представник кожної команди «захищає» роботу біля дошки (4 учня одночасно). Решті учнів пропонується записати в робочі зошити ту задачу (або її частину), яка на його думку викликала найбільше труднощів.

Задача № 4 розв’язується двома способами.

ЗАДАЧА № 1

З деякої точки до площини проведені перпендикуляр і 2 похилі. Визначити довжину перпендикуляра, якщо похилі відносяться як 3:4, а їх проекції дорівнюють відповідно  9 см і 16 см.

Розв’язування                                    А

АВ    α

АС, АD-_____________;

ВС і ВD- їх ________________ відповідно;

Так як АС:АD=__________, то                     

 

Нехай АС=______см, АD=______см,

де х- коефіцієнт пропорційності.

Так як більшій похилій відповідає _____________ проекція, то

ВС=_____см, ВD=_____см.

З ∆ АВD (<АВD=_____°) за теоремою Піфагора:

АВ²=_______-________, АВ²=_______-________

Аналогічно, з ∆ АВС: АВ²=_______-________, АВ²=_______-________

Складаємо рівняння:___________=____________

                                ________________________________

                                ________________________________

Тоді АВ²=______________________

АВ=±√_______=±_______(-______ не задовольняє умову задачі).

Відповідь: довжина перпендикуляра _____см.

 

ЗАДАЧА № 2

Телефонний провід завдовжки 15 м протягнуто від телефонного стовпа, де він прикріплений на висоті 8 м від поверхні Землі, до будинку, де його закріпили на висоті 20 м. Знайдіть відстань між будинком і стовпом, вважаючи, що провід не провисає.

Розв’язування

Математична модель поверхні Землі -     С

площина ____,

а відстані 8 м і 20 м від             15 м

поверхні Землі –

прямі, що ___ площині ___.

                                         В

 За властивістю             8м                    F

прямих і площин:

АВ ____СD.

 

Проведемо

BF___AD, тоді  BF=____

і ∆BCF=_________________(<BFC=____°)

CF=____________.

За теоремою _____________: BF²=________________________________

                                           BF=±√ ____=±_____ (____ не задовольняє умову задачі).

Відповідь: відстань між будинком і стовпом _____м.

 

ЗАДАЧА № 3

Над квадратною будівлею розміром 12 м×12 м потрібно виготовити дах, найвища точка якої знаходиться на висоті 3 м над основою даху. Якою повинна бути довжина основних балок ?

                                                                                  S

Розв’язування B                            C

  Аналіз умови задачі:                                                               

Всі вершини квадрата повинні                         

Знаходитися на однаковій відстані 

від найвищої точки даху. A                         D

Тому маємо математичну модель:

OS ┴ площині квадрата,

SD- похила, OD-її _______________

Діагональ квадрата BD=_________ м, ВО= =____ м

З ∆SOD (<______=90°) за теоремою ________________:

SD²=2²+ ______=_______________________

SD=±√_______=±_____ (____ не задовольняє умову задачі).

Відповідь: довжина кожної основної балки ____ м.

 

ЗАДАЧА № 4

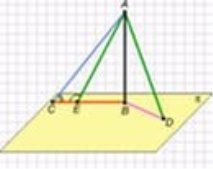
З точки М, що міститься від площини α на відстані МО=4, проведені до цієї площини похилі МА, МВ і МС під кутами 30°, 45° і 60° відповідно до прямої МО, МО┴α. Порівняти довжини похилих ?

Розв’язування M

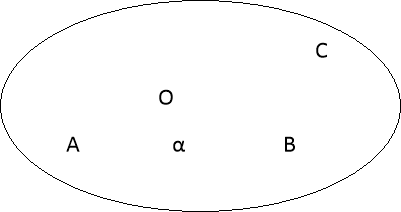Так як перпендикуляр і

три похилі проведені

з 1 точки до 1 площини, то 

з трьох похилих більше та,

_______________ якої

_______________.

 

МО=4 - катет, прилеглий

до кута між перпендикуляром ______ і похилими ______,______

і______, тому довжини похилих обчислюється за формулами:

 АМ=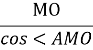 ( З ∆AOM, < AOM=______°), АМ=----------------

ВМ=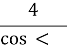  =___________( З ∆ВOM, < ВOM=______°),

СМ=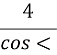  =___________( З ∆СOM, < СOM=______°).

Відповідь:________<________<________

 

 

Колективне розв’язування усних задач.

1.Назвіть геометричне місце основ похилих даної довжини, проведених з однієї точки до площини

2. Новорічну ялинку часто встановлюють на хрестовині. А як розміщують стовбур до кожної планки хрестовини ? Чому ?

3. Чи можна стверджувати, що спільне ребро двох стін перпендикулярно до підлоги. Чому ?

4. Яким є взаємне розміщення двох прямих, якщо вони перпендикулярні  до однієї площини ? (прямі паралельні).

5. З двох різних точок до площини проведено дві рівні похилі. Чи можна стверджувати, що проекції цих похилих на дану площину рівні ?

6. Запропонуйте спосіб розпилювання дерев’яного бруска в точці А перпендикулярно до його ребра. Продемонструйте на моделі.

7. Як на практиці за допомогою виска перевірити вертикальність встановлення стовпа? На чому ґрунтується ця перевірка?

 

VІ. Домашнє завдання.

Скласти задачу прикладного змісту на застосування теореми Піфагора в просторі.

 

 

 

 

 

 

VІІ. Підбиття підсумків уроку.

Виконання «Графічного диктанту» (фронтально).

Учні записують в робочих зошитах відповіді на запитання диктанту, користуючись символами «так»-∩,

«ні»- ─, а потім здійснюють самоперевірку за ключем – відповіддю, запропонованим вчителем.

1. З даної точки до даної площини можна провести перпендикуляр, і тільки один.
2.  Діагональ квадрата зі стороною 3 см дорівнює 3√2 см.
3.  Якщо дві площини перпендикулярні до однієї прямої, то вони паралельні.
4. Перпендикуляр завжди більше похилої.
5. Якщо довжина похилої дорівнює 5 см, а її проекція – 4см, то довжина перпендикуляра, проведеного з тієї ж точки до даної площини дорівнює 3 см.
6. Якщо пряма, що лежить в площині і проходить через основу похилої, перпендикулярна похилій, то вона перпендикулярна і перпендикуляру.
7. Дві прямі називаються перпендикулярними, якщо вони перетинаються.
8. За теоремою Піфагора: в прямокутному трикутнику квадрат гіпотенузи дорівнює сумі квадратів катетів.

 

Ключ – відповідь:

∩∩∩─∩─ ─∩

    123 456 7 8

Визначення найактивніших учнів і команд, оголошення оцінок.

 

 

« Математика цікава тоді,

                                                коли дає поживу нашій

                                        винахідливості й

здатності до міркувань.»

 

Д. Пойа