Виникнення і розвиток стереометрії. Аксіоми та наслідки з них.

Тема уроку. Виникнення і розвиток стереометрії. Аксіоми та наслідки з них.

Мета уроку: розширити і систематизувати відомості учнів про властивості основних геометричних фігур на площині і в просторі.

Освоївши матеріал уроку учні повинні:

знати:

• аксіоми стереометрії та наслідки з них;
• аксіоматичну побудову геометрії;

вміти:

• застосовувати аксіоми та наслідки з них до розв’язування геометричних і практичних задач.

Хід уроку

І. Вступ

Логічна побудова геометрії

Кожна наука і кожний навчальний предмет у школі оперують певним колом понять, вивчають їх властивості і відношення між ними. Наприклад, фізика вивчає такі поняття, як рух, швидкість, маса, теплота, струм тощо. Граматика оперує поняттями: речен­ня, прикметник, дієслово тощо. Геометрія – це наука про власти­вості геометричних фігур, і вона має справу з такими поняттями, як геометрична фігура.

– Які ви знаєте види фігур?

Наприклад, трикутник, круг, куб.

– Які відношення між фігурами вивчає геометрія?

Такі відношення між фігурами, як рівність, по­дібність, паралельність, перпендикулярність.

– Назвіть розглядувані пе­ретворення фігур.

Наприклад, симетрія, поворот, подібність.

– З якими  геометричними величинами має справу?

Це довжини відрізка, кола, градусна міра кута, площа, об'єм.

На відміну від інших наук геометрія має специфіку в своїй побудові. Вона побудована дедуктивно.

– Що це означає?

Дедукція (від лат. deduction – виведення) у широкому розумінні – це така форма мислення, коли нова думка виводиться суто логічно з деяких даних думок-посилань. У вужчому розумінні дедукція – це такий умовивід, внаслідок якого одержуються нові знання про предмети або групи предметів на основі вже наявних знань про досліджувані предмети.

– Що вивчає планіметрія? Які її найпростіші фігури?

У планіметрії вивчаються фігури на площині. Найпростішими фігурами в планіметрії є точка і пряма.

Ці два поняття належать до первісних понять, яким умовились не давати означень і використовувати їх при означенні інших по­нять. Наприклад, серединним перпендикуляром до відрізка називається пряма, яка перпендикулярна до цього відрізка і проходить через його середину. Тут серединний перпендикуляр означається через первісне поняття «пряма».

Потреба в первісних поняттях і їх роль в геометрії саме і пов'язані з дедуктивним характером її побудови. Справді, в гео­метрії кожне нове поняття, крім первісних, означається або на основі первісних, або на основі раніше означених понять. Розглянемо ще один приклад.

– Що називають квадратом?

Як відомо, квадратом називають пря­мокутник, у якого всі сторони рівні.

– Через яку фігуру означається прямокутник?

Прямокутник означається че­рез паралелограм, у якого всі кути прямі.

– Дайте означення паралелограма.

Паралелограм означаєть­ся через чотирикутник.

Маємо ланцюжок понять, який не може бути нескінченним. Тому виникає потреба невели­ку кількість понять прийняти без означення (первісні поняття), а через них означати інші.

 квадрат 

 

 прямокутник

 

 паралелограм

 

 первісні поняття

 

 

 

Крім точки і прямої, первісними поняттями планіметрії є по­няття „належати” для точок і прямих, „лежати між” – для трьох точок прямої, „довжина відрізка”, „градусна міра кута”. Первісні поняття, як і біль­шість означуваних, походять від об'єктів, що існують реально, і є абстракцією від них. Наприклад, поняття „площина” походить від реальної поверхні кришки стола або поверхні озера. Однак площину ми уявляємо необмежене продовженою, вона не має товщини.

– Від якого реального об’єкта абстрагують пряму?

Пряма образ туго натягнутої нитки або дроту. Проте пряма в геометрії не має кінців і уявляється необмежене продов­женою, вона не має товщини.

Крім первісних і означуваних понять геометрія оперує твер­дженнями, що виражають властивості понять. Вони бувають двох видів: аксіоми і теореми. Твердження, що виражають властивості найпростіших фігур (первісних понять) і приймаються без дове­дення, називаються аксіомами. Твердження, що виражають влас­тивості геометричних фігур і доводяться, мають назву теорем. Потреба і роль аксіом теж спричинені дедуктивним характером побудови геометрії. Тут ми маємо аналогічну схему, бо кожне нове твердження доводиться на основі раніше відомого, вже доведеного твердження і т. д. Оскільки ланцюжок тверджень не може бути нескінченним, виникає потреба невелику їх кіль­кість умовитись прийняти без доведення і використовувати при доведенні інших.

•  Пригадаємо аксіоми планіметрії, скориставшись для цього таблицею.

–  Проаналізуємо означення „Суміжні кути” з по­гляду того, через які раніше відомі поняття воно формулюється. Пригадаємо його.

Два кути називаються суміжними, якщо одна їх сторона спільна, а інші сторони цих кутів є додатковими півпрямими.

– Через які поняття воно означається?

Воно означається через поняття сторона кута та півпряма.

– Виділимо основні поняття, відношення та величини.

Основні поняття: точка і пряма, основні відношення: лежати між, лежати на, основні величини: градусна міра кута.

– Як висновок, розглянемо наступну схему побудови геометрії.

1. Перелічуються первісні (неозначувані) поняття.
2. Формулюються аксіоми про властивості первісних понять.
3. За допомогою первісних та раніше означених понять фор­мулюються означення нових понять.
4. На основі аксіом, доведених раніше тверджень і означень доводяться нові твердження.

 

 

 

 

 

 

ІІ. Вивчення аксіом стереометрії та наслідків з них.

Стереометрія – це розділ геометрії, що вивчає фігури у просторі. Найпростішими фігурами простору є:

• точка: А, В, С,...
• пряма: а, в, с,...
• площина: 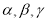,..., (АВС).

Термін „стереометрія” походить від гр. – об'ємний, просторовий і – вимірюю. Оскільки пло­щина – нова найпростіша фігура, то треба сформулювати аксіо­ми, що виражають властивості площини. Розглянемо три аксіоми стереометрії, зведені в одну таблицю.

Оскільки точка і пряма також є основними фігурами простору, то всі аксіоми планіметрії переходять у стереометрію і систе­ма аксіом стереометрії складається з дев'яти аксіом планімет­рії і трьох аксіом групи С.

У планіметрії ми мали одну площину, на якій розташовувались всі розглядувані нами фігури. У стереометрії нескінченно багато площин. У зв’язку з цим формулювання деяких аксіом планіметрії в якості аксіом стереометрії вимагають уточнення. Це стосується аксіом IV, VII, VIII, IX.

IV. Пряма, що належить площині, розбиває цю площину на дві півплощини.

VII. Від півпрямої на площині, що її містить, у задану півплощину можна відкласти кут з заданою градусною мірою, меншою 180^○, і лише один.

VIII. Який би не був трикутник, існує рівний йому трикутник у даній площині у заданому розташуванні відносно даної півпрямої у цій площині.

ІХ. На площині через дану точку, що не лежить на даній прямій, можна провести не більше однієї прямої, паралельної даній.

Наслідки з аксіом

Теорема 1. Через пряму і точку, що належить даній прямій, можна провести площину, і притому тільки одну.

 Дано: пряма а, точка В а.

 Довести: 1) існує {а, В};

          2) єдина.

 

Доведення

1) Виберемо на прямій а довільну точку А. Проведемо пряму в  {А;В} (аксіома І). а і в різні, оскільки В а. За аксіомою С3: а і в визначають площину .

У ході доведення вчитель разом з учнями шляхом системи запитань складає таблицю.

– Яка аксіома стереометрії обґрунтовує можливість проведення площини?

– На яку додаткову побудову наштовхує нас ця аксіома?

– Яка аксіома обґрунтовує можливість проведення прямої?

– Через які точки проведемо ще одну пряму?

– Яка аксіома обґрунтовує можливість вибору точки А?

Твердження	Обґрунтування
Виберемо на прямій а довільну точку А Через А і В можна провести пряму в Прямі а і в різні Через прямі а і в можна провести площину Площина проходить через пряму а і точку В	1. За аксіомою про існування точок, які належать прямій 2. За аксіомою про можливість проведення прямої через дві точки 3.  Оскільки точка В не належить прямій а 4.  За аксіомою про можливість проведення площини через дві прямі, які мають спільну точку 5.  Тому що проходить через а за побудовою, а через В, тому що В належить в; проходить через в за побудовою

 

2) Доведемо єдиність (методом від супротивного).

Нехай існує ще одна площина , що проходить через а і точкуВ. За аксіомою С2: точка В належить прямій а. Це суперечить умові, що В  а. Припущення не вірне.

 Теорему доведено.

Теорема 2. Якщо дві точки прямої належать площині, то вся пряма належить цій площині.

А |

 .

В |

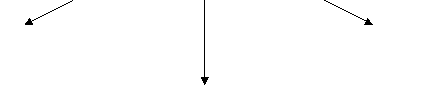Наслідок.     Пряма і площина 

 

не перетинаються

(немає спільних точок)       перетинаються 

  (мають одну спільну точку)                           

       (принаймні дві

спільні точки)

(Цю теорему учні доводять зі складанням таблиці і оформлюють вдома самостійно).

Теорема 3. Через три точки, що не лежать на одній прямій, можна провести площину, і притому тільки одну.

 Дано: а.

 Довести: 1) існує ;

        2) – єдина.

Учитель разом з учнями складає таблицю – колективний пошук доведення, оформлюють доведення учні вдома самостійно.

Твердження	Обґрунтування
Проведемо прямі АВ і АС     Прямі АВ і АС різні   Через прямі АВ і АС можна провести площину   Точки А, В, С належать площині	За аксіомою про можливість проведення прямої через дві точки   Точки А, В і С не лежать на одній прямій   За аксіомою про можливість проведення площини через дві прямі, які мають спільну точку   Точки А, В і С належать до прямих АВ і АС, а вони належать площині за побудовою

 

 

 

Доведення.

1) Проведемо прямі АВ і АС, вони різні, оскільки а. За аксіомою С3: через прямі АВ і АС можна провести площину .

2) Доведемо єдиність.

За теоремою 2 (якщо дві точки прямої належать площині, то вся пряма належить цій площині): . За аксіомою С3 така площина єдина.

Теорему доведено.

ІІІ. Задачі на доведення

Задача 1. Точки А, В, С і Д не лежать в одній площині. Доведіть, що прямі АВ і СД не перетинаються.

Доведення.

• Скористаємось методом від супротивного.
• Яке можемо зробити припущення?
• Маємо дві прямі, що перетинаються. Яке з щойно вивчених тверджень можемо застосувати?
• Якщо прямі АВ і СД визначають площину 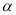, то який висновок можемо зробити щодо точок?
• У чому полягає отримане протиріччя?

Нехай прямі АВ і СД перетинаються, тоді за аксіомою С3: , а це означає, що точки А, В, С і Д лежать в одній площині. Отримали протиріччя з умовою задачі. Значить прямі АВ і СД не перетинаються.

Задача 2. Чотири точки не лежать в одній площині. Чи можуть будь-які три з них лежати на одній прямій.

Доведення.

• Яке можна висунути припущення?
• Яке відоме вам твердження можна застосувати?
• З якою умовою ми отримали протиріччя?

Нехай три точки лежать на одній прямій, а четверта не належить цій прямій. Тоді за теоремою-наслідком 1 можна провести єдину площину, якій належить дані пряма і точка. Це означає, що задані умовою чотири точки належать одній площині. За умовою задачі це не можливо. Значить будь-які три з цих точок не можуть лежати на одній прямій.

IV. Підсумок уроку

Сьогоднішній урок ми присвятили ідеї дедуктивної побудови геометрії, походженню та ролі первісних понять і аксіом, пригадали аксіоми планіметрії, ознайомилися з аксіомами стереометрії та наслідками з них. Завершити урок хочеться прикладами використання аксіом та їх наслідків у виробничій діяльності людини.

1.   Тесляр перевіряє, чи розміщуються кінці ніжок стола в одній площині, від чого залежить стійкість стола. Він натягує нитки на кінці ніжок і перевіряє, чи перетинаються вони (аксіома С3).
2.   Тесляр перевіряє якість поверхні стола, що виготовляється, прикладаючи до кришки в різних напрямках лінійку. Якщо між лінійкою і кришкою стола немає просвітів, то стіл виготовлено якісно (теорема 2).
3.   На теоремі 3 ґрунтується будова штативів для фотоапаратів і різних геодезичних приладів. Кінці ніжок штативів належать одній площині, внаслідок чого прилад займає стійке положення.

Тестові завдання

1. На малюнку зображено куб АВСДА₁В₁С₁Д₁. Знайдіть кути трикутника В₁Д₁С.
2. Як розмістити три прямі так, щоб вони утворили 12 прямих кутів?
3. Чи вірно, що пряма, яка має з колом тільки одну спільну точку, є дотичною до кола в цій точці:

1) на площині;   2) у просторі?

4.  Довести, що через дві довільні точки можна провести хоча б одну площину.

5.  Чи можна стверджувати, що всі точки кола належать площині, якщо це коло має з даною площиною:

 1) дві спільні точки;  2) три спільні точки.

6.  Через три точки можна провести дві різні площини. Як розташовані ці точки?