Збірка "Прикладні задачі. Геометрія.11 клас"
Відділ освіти Тернівського міськвиконкому
Прикладні задачі
в курсі геометрії 11 класу

Вчитель математики
ЗССО № 5 м. Тернівка,
Войтюк Н. М.
Тернівка
2019 рік
Цей посібник – зібрання завдань практичної направленості з теми :„ Об’єми та площі поверхні”.
Наводяться зразки розв’язання задач та завдання для самостійної роботи, до яких наводяться відповіді.
Для вчителів математики, учнів старшого шкільного віку.
Існує таке поняття, як „прикладна математика”, яке трактують як сукупність усіх математичних методів і дисциплін, що застосовується за межами математики. Якщо в давнину геометрія і арифметика представляли всю математику – теоретичну і прикладну, - то до кінця XVIII ст. у зв’язку з проблемами навігації та артилерії виникла необхідність створення математичної теорії руху. Це зробили в своїх роботах німецький математик, фізик, філософ Готфрид Вільгельм Лейбніц (1646-1716) і англійський математик, фізик, механік, астроном Ісак Ньютон (1643-1727) – основоположники математичного аналізу. Майже одночасно потреби демографії, страхування привели до створення початків теорії ймовірності.
Теорія імовірностей, подібно до інших розділів математики, розвинулася з потреб практики: в абстрактній формі вона відображає закономірності, властиві подіям масового характеру. Ці закономірності відіграють надзвичайно важливу роль у фізиці й інших галузях природознавства, військовій справі, найрізноманітніших технічних дисциплінах, економіці й ін.
У XVIII – XIX ст. прикладна математика збагатилася такими галузями, як теорія диференціальних рівнянь, рівняння математичної фізики, елементи математичної статистики.
У багатьох випадках фізичні закони описують деякі співвідношення між величинами, що характеризують певний процес, і швидкість зміни цих величин. Ці закони виражаються рівностями, в яких є невідомі ів Землі, кофункції та їх похідні. Такі рівності називають диференціальними рівняннями. Вони є математичною формулою запису ряду фізичних законів. Диференціальні рівняння – основний математичний апарат у природознавстві. Вони застосовуються в фізиці та астрономії, аеродинаміці і теорії пружності, хімії і економіці, біології та медицині.
Математична статистика, яка виникла спочатку для цілей демографії і страхування , перетворилася в один з основних методів кількісного дослідження явищ природи, технічних процесів, економіки й лінгвістики.
У ХХ ст. сформувалися нов. методи математичного дослідження практичних задач: теорія випадкових процесів, теорія графів, функціональний аналіз, оптимальне управління, лінійне й нелінійне програмування.
Подальше вдосконалення техніки і виробництва пов’язується з розвитком так званої теорії надійності. Теорія надійності вивчає і розробляє методи, яких необхідно дотримуватися під час проектування, зберігання, експлуатації технічних виробів для забезпечення максимальної їх ефективності в процесі використання. Математичною базою теорії надійності, яка є перш за все інженерною наукою, є теорія ймовірностей і математична статистика.
Яскравим прикладом взаємозв’язку математики з практикою є використання сучасної обчислювальної техніки. Завдяки розвитку обчислювальної техніки і електроніки досягнуто великих успіхів у створенні та запуску штучних супутникових та космічних ракет, кораблів і станцій. Відомий український кібернетик В.М. Глушков (1923 – 1982) образно порівняв кібернетику з кільцевою автострадою, яка встановлює зв’язок між десятками науками, які розходяться з неї як з центра.
Важливим напрямком у розвитку математичної мови є створення так званих формальних мов, пов’язаних з обчислювальною технікою і використанням електронних обчислювальних машин для управління виробничими процесами, лініями зв’язку і ін. За допомогою таких мов відбувається спілкування людини з машиною, що передбачає сприймання машиною інформації, яку їй постачають, і відповідні дії машин.
У наш час електронно-обчислювальна техніка є одним з основних засобів проникнення математики в дослідження процесів економіки, природи, техніки й соціальних явищ, вона відіграє важливу роль в автоматизованих системах управління виробничими процесами, а також в автоматизації обладнання.
Математика, як і інші науки, допомагає враховувати ті зміни в навколишньому середовищі, які можуть відбутися у зв’язку з господарською діяльністю людини. Математиками вже розв’язана задача, пов’язана з проектуванням будівництва підприємства на даній території з урахуванням „вигоди” від його функціонування і „втрат” у розумінні зміни оточуючого середовища. Розроблені також математичні методи оцінки екосистем і прогнозування їх станів.
Математика, перш ніж вивчати своїми методами якесь явище, створює його математичну модель, тобто перелічує всі ті особливості явища, які необхідно взяти до уваги. Наприклад, протягом трьохсот років особливості руху планет Сонячної системи з великою точністю передає модель взаємодії двох точок, яка визначається силою взаємодії між ними.
Математичні моделі економічних об’єктів і процесів та методи їх дослідження є предметом теоретичної прикладної науки математичної економіки.
З розвитком виробництва і його ускладненням зросли потреби і в математичних розрахунках. Це і розрахунки планів виробництва, і визначення найвигіднішого розміщення будівельних об’єктів, і вибір економних маршрутів перевезень. Розвиток математичної економіки спонукав до появи математичних теорій, об’єднаних назвою „математичне програмування”.
Одним із розділів сучасної математики є теорія ігор, яка займається прийняттям оптимальних рішень в умовах конфліктів, суперечностей, неповного знання тих обставин, за яких доводиться приймати рішення. Побудова гри є моделлю прийняття рішення, Використання досягнень теорії ігор на практиці пов’язано з різноманітними труднощами, але в цій теорії закладені великі потенціальні можливості застосування.
Навіть цього огляду достатньо для висновку, що математика все глибше проникає у найрізноманітніші галузі людського життя і діяльності, є надійним інструментом пізнання людиною дійсності і перетворення її на своє благо.
Цікавим є думки американського математика М. Стоуна щодо можливостей використання математики для прийняття виважених політичних рішень: „ Можна сподіватися, що одного чудового дня завдяки апаратові математики розв’язання політичне проблем стане більше ґрунтуватися на завданнях і дещо менше здогадках і що світ, у якому ми живемо, функціонувати трохи краще і менше залежатиме від непередбачених подій”.
Отже, математичні знання потрібні не лише тим, хто в майбутньому буде займатися дослідженнями в галузі математики, фізики, астрономії чи інженерної справи, а й тим, хто стане юристом та істориком, агроном чи організатором виробництва, біологом чи лікарем, а також кваліфікованим робітником.
Вирішальне значення має математичний стиль мислення, уміння логічно міркувати, а саме ці якості людина набуває під час навчання математики.
Побуваємо в цехах деяких заводів і фабрик, на будівельних майданчиках, у шахтах та копальнях. Придивимось до людей, які створюють нові машини, видобувають руду і виплавляють метал, піднімають на-гора вугілля, дістають з надр землі нафту і газ. Понад 10000 професій потребує промисловість, а професії глибокого вивчення математики. Не можна уявити собі жодної галузі науки без участі в ній математики. А як може обійтись без математики робітник біля верстата? Виточуючи деталь, він користується кресленням, виконуючи різні розрахунки, користується математичними формулами.
- Знайдіть масу десятиметрової труби діаметром 1420 мм, яку зроблено зі стального листа завтовшки 22 мм. Маса 1 м3 сталі 7600 кг.
Розв’язання:
R1 – радіус зовнішнього циліндра;
R2 – радіус внутрішнього циліндра.
- V1 = π R12Н,
R1 = ![]() = 710(мм) = 0,71 (м)
= 710(мм) = 0,71 (м)
V2 = π R22Н,
R2 = 0,71 – 0,022 = 0,688 (м).
Тоді об’єм труби дорівнює:
V = V1 – V2 ,
V = π R12Н - π R22Н =π Н(R12 - R22) = π Н(R1 - R2)( R1 + R2),
V = 3,14![]() (м3).
(м3).
-
M = 7600
 (кг) = 7,6 (т).
(кг) = 7,6 (т).
Відповідь: 7,6 т.
2. Мідна заготовка довжиною 270мм і діаметром 25мм витягується в дріт довжиною 75см. Знайдіть діаметр цього дроту.
Розв’язання:
- d1 – діаметр заготовки,
h1 – її довжина; h2 – довжина дроту, d2 – його діаметр.
V1 =![]() , V2 =
, V2 =![]()
Оскільки V1 = V2, то
d22 = ![]() , d2 = d1
, d2 = d1![]() . d2 = 25
. d2 = 25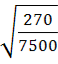 = 15 (мм).
= 15 (мм).
Відповідь: 15 мм.
3. Мідний циліндр, радіус основи якого дорівнює 12 см, треба обточити так, щоб його маса стала вдвічі меншою. Якої товщини треба взяти мідний циліндр?
Розв’язання:
- Нехай радіус мідного циліндра дорівнює R, а стального – r, тоді V = π R2Н, V1 = πr2Н.
- Оскільки маса циліндра стала вдвічі меншою, то
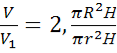 = 2,
= 2, ![]()
r2 = ![]() , r =
, r = ![]() ,
,
r = 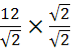 = 6
= 6![]() (см).
(см).
-
R – r = 12 – 6
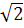 = 1208,58
= 1208,58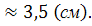
Відповідь: 3,5 см.
4. Рівносторонній циліндр розплавили і виготовили куб. як змінилася при цьому площа поверхні?
Розв’язання:
- За умовою Н = 2R (циліндр – рівносторонній).
- Vц = Vк ,
Vц = π R2Н = 2πR3,
Vк = a(а – довжина ребра куба),
2πR3 = а3, а = ![]()
- Sп = 2πR2R + 2πRН,
Sц = 2πR2 + 4πR2 = 6πR2,
Sк = 6а2, Sк = 6(3![]() )2 R2.
)2 R2.
-
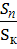 =
= 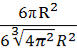 =
= 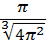 =
= 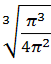 =
= 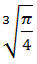 < L
< L
Відповідь: Площа поверхні куба стала більшою.
5. 25 м стрічки завтовшки 0,1 мм намотали щільно на картонну трубку – отримали валик діаметром 1 дм. Який діаметр трубки?
Розв’язання:
Площа поперечного перерізу валика дорівнює 25π см2, стрічка заповнює площу 25 см2, тому серцевина має площу 25( π – 1) см2. Позначимо діаметр трубки ― d (без стрічки); тоді з рівняння
π![]() = 25(
= 25(![]()
маємо, що
d = 10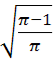 см
см ![]() 8,26 см.
8,26 см.
Відповідь: 8,26 см
6.Знайдіть місткість сараю, який має форму прямокутного паралелепіпеда, з двопологим дахом і прямим кутом між кроквою, якщо довжина сараю a=12,5 м, ширина b=7,6 м, висота усього приміщення h=7,3 м.
Розв’язання:
-
V
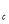 = a∙b∙c, V
= a∙b∙c, V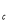 = 7,6
= 7,6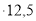
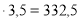 (м
(м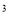 ).
).
- Дах – трикутна призма, основою якої є прямокутний рівнобедрений трикутник. Тоді висота призми 12,5 м, довжина гіпотенузи основи 7,6 м, а висота, що проведена до гіпотенузи, дорівнює 7,3-3,5=3,8 (м)
V![]() =
= ![]() 3,8
3,8![]() 180,5 (м
180,5 (м![]() )
)
- Тоді об'єм усього приміщення :
V=V![]() +V
+V![]() ,
,
V=180,5+332,5=513 (м![]() ).
).
Відповідь: 513 м![]()
7.Силосна вежа має форму правильної восьмикутної призми, сторона основи якої дорівнює 2,9 м, висота призми 8,2м. Скільки тонн силосу може вмістити вежа? (Питома вага силосу 0,8)
Розв’язання :
1). a![]()
![]() R sin
R sin![]() ,
,
a![]() R sin22
R sin22![]() ,
,
R=![]() (м)
(м)
2). S![]()
![]() ,
,
S![]()
3). V=S![]() ,
,
H=8,2м,
V=![]()
![]()
4). m=pV,
m=![]()
Відповідь: 265т
Щоб посіяти зернові культури, треба під них відвести ділянку певної площі, потім у встановлений термін обробити цю землю і засіяти її зерном. Знаючи лану і врожай, зібраний з одного гектара, можна підрахувати, скільки всього буде зібрано зерна. Для зберігання зернових та інших культур потрібні приміщення. Скільки їх треба збудувати і якого об’єму ? Відповіді на ці питання дають математичні розрахунки. Для зимівлі худоби треба зробити запаси кормів. А якої місткості повинна бути силосна вежа, силосна башта? На це теж відповість математика.
8. Конусоподібна купа зерна має висоту 2,4 м, а довжина кола основи 20м. Скільки тонн зерна в купі, якщо вага
1м![]() дорівнює 750кг?(19т)
дорівнює 750кг?(19т)
9. Обчислити масу силосу (у тонах), що знаходиться в силосній ямі циліндричної форми, діаметр основи ями 6,8м, а її глибина 4,3м. (Маса 1 м![]() силосу 670кг). (10,5т)
силосу 670кг). (10,5т)
Політ нескінченна шеренга складних математичних задач, що визначають можливі, потрібні й безпечні траєкторії польоту й фігури пілотажу за кожною з численних операцій, що супроводжують зліт, політ і посадку літака─сотні вимірювань фізичних і геометричних величин. Розв’язування багатьох рівнянь і нерівностей забезпечує надійність польоту. Складні розрахунки потрібні для визначення орбіти космічного корабля, шляху виводу його на орбіту і спуску на землю з урахуванням опору атмосфери і відхилення форми Землі від кулі.
10. Перший радянський штучний супутник Землі мав вигляд кулі із зовнішнім діаметром 58см. Визначте площу поверхні супутника. (1м2).
11. Штучні супутники Землі мають форму кульок, діаметри яких дорівнюють відповідно 58 і 16 см. У скільки разів об’єм одного з них більший за об’єм іншого? (У 48 разів).
12. Якщо прийняти за одиницю діаметр Землі, то діаметр Місяця складає 3 цієї одиниці. Знайдіть співвідношення
площ поверхонь Місяця та Землі.
Математика стоїть на варті миру і має величезне значення для оборони країни. Без математики неможливо збудувати військові кораблі та підводні човни, що охороняють спокій наших водних кордонів. Хіба можна без знань математики побудувати могутні ракети, що оберігають мирну працю наших людей? Звичайно, ні! А чи потрібні солдату знання математики? Так.
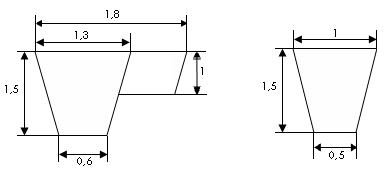
13.Скільки потрібно солдат для того, щоб викопати за 8 год. траншею довжиною 25м хід сповіщання такої самої довжини, враховуючи, що кожний солдат за годину має викопати 0,75м3? Профіль траншеї і ходу сповіщання і розміри в метрах дані на рисунках.
 РОЗВ’ЯЗАННЯ
РОЗВ’ЯЗАННЯ
1.Одна частина траншеї має вигляд призми, основою якої є трапеція:
V1=SТР.∙Н,
V1= (1.3+0.6) / 2) ∙1.5=1.425( м3),
V=1.425∙25= 35.625(м3).
2.Друга частина траншеї має вигляд призми, основою якої є паралелограм:
V2=SПАР. * Н,
SПАР.. =(1.8 – 1.3)∙ 1= 0.5(м3),
V2 = 0.5 ∙ 25 = 12.5(м3).
3.Хід сповіщання має вигляд призми, в основі якої лежить трапеція:
V3= Sтр. ∙Н,
SТР. = (1+0.5) / 2) ∙ 1.5 = 1.125 (м3),
V3 = 1.125∙25= 28.125(м3).
4. V= V1 + V2 + V3,
V= 36.625+12.5+28.125= 76.25(м3).
5.За 8 годин: 8∙0.75 м3= 6м3, тоді 76.25 / 6=13(солдат).
Відповідь: Потрібно 13 солдат
У різних галузях промисловості потрібні різної форми цистерни, ємкості, пакунки тощо. Але, щоб їх виготовити, також потрібні знання геометричних формул об’єму і площ поверхонь геометричних тіл. Розглянемо декілька задач.
14.Резервуар для води складається з півкулі радіусом 35см і циліндра з таким самим радіусом основи. Якої висоти повинна бути його циліндрична частина, щоб об'єм усього резервуара дорівнював 167л?
Розв'язання
1.Розглянемо резервуар –циліндр радіусом R і висотою H, його об'єм дорівнює V1=![]() R²H.
R²H.
2.Розглянемо півкулю, її об'єм дорівнює V=![]() ³
³
3. Об'єм резервуара дорівнює сумі об'ємів циліндра та півкулі.
V=![]() ²
²![]() ³;
³;
4. ![]() ²H=V-
²H=V-![]() ³,
³,
![]() ²
²![]() ;
;
-
H=
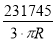 ;
;
6.![]() (см)
(см)
Відповідь:20 см.
15.Посудина має вигляд зрізаного конуса, висота якого 27м, а довжина обхвату 66см і 96 см. Скільки літрів вміщує посудина?(14,9л)
16.У циліндричну цистерну ємністю 12 м³ налито пальне. Скільки пального міститься у цистерні?
17.Вафельний стаканчик для морозива має форму конуса, радіус якого 6 см ,а бічна довжина стаканчика 10см.Який об'єм морозива ,якщо покласти його рівно по краї.
Це цікаво знати
„ Геометрія бджолиних сот „
„ Бджолині соти абсолютно досконалі з точки зору економії праці і воску ,” – писав Ч. Дарвін. Їх вигляд зверху – правильний шестикутник. Доведено, що він з усіх можливих многокутників заданої площі має найменший периметр. Тоді кожна сота в цілому є відкритою зверху шестикутною призмою з хитромудро добудованим дном. Таким чином, і площа її поверхні теж найменша з можливих.
„ Дещо про форму сиру „
Рецептура виготовлення сиру і його смакові якості значною мірою визначаються формою. При цьому сировари знають, що за рівного об’єму сири кулястої форми мають меншу площу поверхні, ніж сири циліндричної форми, тому на прилавках ми все частіше їх бачимо.
„ Конуси в природі „
Сипучі матеріали в природі часто набувають форми конуса. Але, що цікаво, ці конуси завжди мають цілком певний кут нахилу твірної до площини Землі – так званий кут природного укосу. Для картоплі він 450, вугілля - 420 , грунту - 400, піску – 250 . Окрім того, в житті користуються не довжиною твірної, а довжиною перекиду
(двох твірних), який виміряти значно легше.
Література
1. Кушнір І. А. Трикутна піраміда у задачах . Либідь –
Київ , 1994.
2. Василевський А. Б. Усні вправи з геометрії.
Народна асвета . - Мінск , 1983.
3. Возняк Г. М. Прикладні здачі на екстремуми.
Проcвещение – Москва, 1985 .
4. Прасолов В. В. Задачі по геометрії .- Головна
редакція фізико -математичної літератури. –
Москва,91.
5. Кожабаєв К. Г. Про виховну спрямованість
математики. Просвещение – Москва, 1988.
6. Гоман О. Г , Грищенко В. М. та інші . Прикладна
механіка. Завдання та тести. Генеза – Київ, 1993
7. Бродський Я. С. Павлов О. Л. Сліпенько А. К.
Тематичне оцінювання з теми „ Геометричні тіла і
поверхні” Математична газета. – 2007. - № 10.
1


про публікацію авторської розробки
Додати розробку
