Збірник контрольних робіт з геометрії, 8 клас

Комунальний заклад

“Маріупольська загальноосвітня школа I-III ступенів №15

Маріупольської міської ради

Донецької області”

 

 

 

 

Збірник контрольних робіт з геометрії

8 клас

 

 

 

 

Г.Ф. Леус

М.О. Михайлова

 

 

 

 

 

 

 

Маріуполь

2020р

Вступ

Навчальний посібник «Збірник контрольних з математики. Геометрія. 8 клас» призначений для тематичного оцінювання досягнень учнів з геометрії в 8-х класах загальноосвітніх навчальних закладів.

Зміст завдань відповідає програмі Міністерства освіти і науки України за чиним державним стандартом.

Збірник містить 7 контрольних робіт, кожна з яких включає два рівноцінних варіанти. Кожен варіант складається з трьох частин, які відрізняються як формою завдань, так і їх складністю:

• I частина (загальна кількість – 5 балів) містить завдання і вправи (під номерами 1-3), 1-2 завдання в основному, репродуктивного характеру на 1-2 логічних кроків, представлених у формі тестів з вибором однієї правильної відповіді. 3 завдання – це завдання на відповідність ( загальна кількість – 3 бали), треба підібрати для кожного з 3-рьох завдань правильну відповідь А – Д. Для їх вирішення учням досить знати правила, формули і визначення, передбачені  програмою, а також вміти виконувати найпростіші перетворення, спрощення та обчислення. Запропоновані завдання відповідають I-II рівню навчальних досягнень учнів.
• II частина (загальна кількість – 4 бали, кожне завдання по 2 бали) містить завдання (під номерами 4-5) III рівня навчальних досягнень учнів. Учень самостійно застосовує знання в стандартних ситуаціях, вміє виконувати математичні операції, загальна методика і послідовність яких йому відома, але зміст та умови змінні.
• III частина (загальна кількість – 3 бали) містить завдання IV рівня навчальних досягнень учнів (під номером 6). Учні приводять запис рішення з обґрунтуванням кожного його етапу і дають вірну відповідь.

 

 

 

 

 

 

 

 

 

 

 

Тема 1. Чотирикутник. Паралелограм. Прямокутник. Квадрат. Ромб.

Варіант 1

 

1. Один з кутів паралелограма дорівнює 42°. Знайти кути паралелограма:

А) 140°, 42°, 140°    Б) 138°, 42°, 138°   В) 139°, 42°, 139°  Г) 138°, 43°, 138°

2.  Сторона ромба – ціле число. Укажіть число, яке може бути значенням периметра ромба:

А) 15      Б) 49     В) 27      Г) 28

 

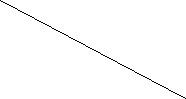
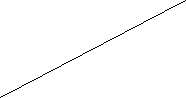
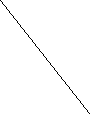
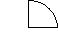
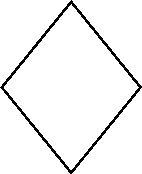
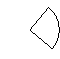
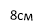3. Знайти відповідність між відомими елементами чотирикутника (мал.1-3) і його периметром ( А-Д) :

 

1)

      А) 32 см

      Б) 38 см

2)       В) 28 см

      Г) 42 см

      Д) 48 см

 

 

3) 

 

 

 

4. Периметр паралелограма дорівнює 56 см. Знайдіть його сторони, якщо одна з них на 6 см більше за другу.
5. Сторона прямокутника 4 см і утворює з діагоналлю кут 60°. Знайти цю діагональ.
6. У паралелограмі ABCD бісектриса кута D перетинає сторону AB у т. Р. Відрізок AP менший від  ВР в 6 разів. Знайдіть периметр паралелограма, якщо АВ = 14 см.

 

 

 

 

Тема 1. Чотирикутник. Паралелограм. Прямокутник. Квадрат. Ромб.

Варіант 2

 

1. Діагональ ромба утворює з однієї з його стороною кут 20°. Знайти градусну міру більшого кута ромба:

А) 150°      Б) 140°     В) 160°    Г) 120°

2. Сторона квадрата – ціле число. Укажіть число, яке може бути значенням периметра квадрата:

А) 35      Б) 59     В) 12      Г) 75

 

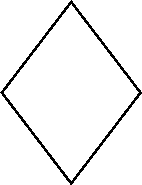
3.    Знайти відповідність між відомими елементами чотирикутника ( мал. 1-3) і його висотою ВМ (А-Д ) :

 

1)

      А) 10 см

      Б) 8 см

2)       В) 9 см

      Г) 11 см

      Д) 5 см

 

 

3) 

 

 

 

 

4. Периметр паралелограма дорівнює 16 см. Знайдіть його сторони, якщо одна з них в 3 рази більше за другу.
5. Діагональ прямокутника утворює з однією з стороною кут 40°. Знайти гострий кут, утворений при перетину діагоналей прямокутника.
6. Сума відстаней від точки перетину діагоналей прямокутника до двох його сусідніх сторін дорівнює 27см. Знайдіть сторони прямокутника, якщо вони відносяться як 4:5.

 

Тема 2. Середня лінія трикутника. Трапеція. Вписані и описані чотирикутники.

Варіант 1

 

1. Основи трапеції 8см і 10 см. Знайти середню лінію трапеції:

А) 11 см      Б) 9 см     В) 12 см    Г) 5 см

 

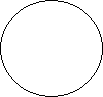
2.                                    ∠ABC = 32°.  Знайти ∠AОC

А) 16°  Б) 32°   В) 64°   Г) 18°

 

 

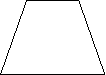
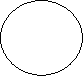
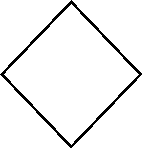
3. Установіть відповідність між елементом ВМ (мал. 1-3) та радіусом вписаного кола в чотирикутник(А-Д).

 

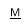1. А) 8 см

Б) 5 см

В) 3 см

Г) 4 см

Д) 6 см

2)

 

 

 

3)

  

 

 

 

4. У колі проведено діаметр АВ і хорду АС. Знайдіть кут ВАС, якщо градусні міри дуг ВС і АС відносяться як 7:2
5. Чотирикутник АВСD вписаний у коло ∠A=110°, ∠В=50°. Знайдіть ∠С і ∠D
6. Діагональ рівнобедреної трапеції є бісектрисою її гострого кута. Знайдіть середню лінію трапеції, якщо її основи відносяться як 3:5, а периметр трапеції дорівнює 42см.

 

 

Тема 2. Середня лінія трикутника. Трапеція. Вписані и описані чотирикутники.

Варіант 2

 

1. Основи трапеції 9см і 11 см. Знайти середню лінію трапеції:

А) 12см      Б) 8см     В) 10см    Г) 20см

 

2.                                    ∠AОВ = 48°.  Знайти ∠AСВ

А) 96°  Б) 72°   В) 16°   Г) 24°

 

 

3. Установіть відповідність між радіусом вписаного кола в чотирикутник(мал. 1-3) і елементом BM (А-Д).

 

2. А) 14 см

Б) 6 см

В) 16 см

Г) 12 см

Д) 20 см

2)

 

 

 

3)

  

 

 

 

4. Точки А,В,С ділять коло на три дуги так, що  ͝  АВ:͝  АС:͝  АС=3:5:7. Знайдіть кути трикутника АВС
5. Чотирикутник MNРK вписаний у коло ∠M=105°, ∠N=65°. Знайдіть ∠P і ∠K
6. У рівнобічній трапеції гострий кут дорівнює 60°, а бічна сторона 16см. Знайдіть основи трапеції, якщо їхня сума дорівнює 38см.

 

 

Тема 3. Подібність трикутників.

Варіант 1

 

1. ΔАВС ~ ΔА1В1С1. Сторони ΔАВС дорівнюють 4см, 10см, 8см. Найменша сторона ΔА1В1С1  дорівнює 10см. Чому дорівнює коефіцієнт подібності:

А) 2       Б) 2,5     В) 3    Г) 0,5

2.  ВD – бісектриса ΔАВС. Знайдіть довжину сторони АВ, якщо ВС=6см,  DС=4см,   АС = 14см.

А) 10      Б) 12     В) 18    Г) 15

3. Установіть відповідність між ознаками подібності Δ-ка і відомими елементами трикутника:

1) I ознака подібності трикутників   А) за трьома рівними кутами

Б) за двома пропорційними сторонами і кут між ними

2) II ознака подібності трикутників  В) за двома пропорційними сторонами

Г) за трьома пропорційними сторонами

3) III ознака подібності трикутників  Д) за двома рівними кутами

 

4. Відрізки АВ і СD перетинаються в точці О. , DВ = 15см. Знайдіть довжину відрізка АС.

5. Медіани АМ і BN ΔАВС перетинаються в точці О. Знайдіть довжини цих медіан, якщо ВО=4см,ОM=3см.

6. Сторони трикутника дорівнюють 6см,9см,12см. Знайдіть периметр подібного йому трикутника, якщо сума найменшої та найбільшої сторін дорівнює 6см.

 

 

 

 

 

 

 

 

Тема 3. Подібність трикутників.

Варіант 2

 

1. ΔMNP ~ ΔM1N1P1. Сторони ΔM1N1P1    дорівнюють 6 см, 9см, 12см. Найбільша сторона ΔMNP дорівнює 18 см. Чому дорівнює коефіцієнт подібності:

А) 3       Б) 2     В) 1,5    Г) 2,5

2.  АD – бісектриса ΔАВС. Знайдіть довжину сторони АС, якщо АВ=9см, ВС=10см, ВD = 4см.

3. Установіть відповідність між ознаками подібності Δ-ка і відомими елементами трикутника:

1) I ознака подібності трикутників   А) за двома рівними кутами

       Б) за двома пропорційними сторонами

2) II ознака подібності трикутників  В) за трьома рівними кутами

Г) за двома пропорційними сторонами і кут між ними

3) III ознака подібності трикутників  Д) за трьома пропорційними сторонами

 

4. Продовження бічних сторін АВ і СD трапеції АВСD перетинаються в т.Е. Більша основа АD трапеції дорівнює 12см; АЕ=15см, ВЕ=5см. Знайдіть меншу основу трапеції.

5. Медіани ВМ і СК ΔАВС перетинаються в точці О. Знайдіть довжини цих медіан, якщо ВО=6см,КО=5см.

6. Сторони трикутника відносяться як 7:6:3. Знайдіть сторони подібного йому трикутника, якщо різниця його найбільшої та найменшої сторін дорівнює 20см.

 

 

 

 

 

 

 

 

 

Тема 4. Співвідношення між сторони і кутами прямокутного трикутника.

Теорема Піфагора.

Варіант 1

 

1. Знайдіть гіпотенузу прямокутного трикутника якщо катет дорівнює 6см, а протилежний йому кут 60°:

А)      Б)         В)        Г)    

2.  Діагоналі ромба дорівнюють 10см і 24см. Знайти сторону ромба.

А) 68см      Б) 12см   В) 13см    Г) 15см

3. У прямокутному ΔАВС, ∠С=90°, АС=6см, АВ=10см. Встановити відповідність між тригонометричними функціями (1-3) і їх значеннями (А-D):

1) sin∠A      А)

Б)

2) cos∠A     В)

Г)

3) tg∠A     Д)

 

4. У ΔАВС, ∠С=90°, tg∠A=0,75,АВ=15см. Знайдіть периметр трикутника.

5. Один з катетів прямокутного трикутника дорівнює 12см, а інший на 8см менший за гіпотенузу. Знайдіть периметр трикутника.

6. У рівнобедреному трикутнику висота, що проведена до бічної сторони, поділяє її на відрізки завдовжки 4см і 1см рахуючи від вершини кута між бічними сторонами. Знайдіть основу рівнобедреного трикутника.

 

 

 

 

 

 

 

Тема 4. Співвідношення між сторони і кутами прямокутного трикутника.

Теорема Піфагора.

Варіант 2

 

1. У прямокутному ΔАВС ∠С=90°, ∠А=30°, ВС=16см. Знайти довжину гіпотенузи АВ

А)      Б)         В)        Г)    

2.  У прямокутнику одна сторона 12см, а діагональ 13см. Знайти другу сторону прямокутника.

А) 10см      Б) 5см   В) 11см    Г) 1см

3. У прямокутному ΔАВС, ∠С=90°, ВС=12см, АС=5см. Встановити відповідність між тригонометричними функціями (1-3) і їх значеннями (А-D):

1) sin∠В      А)

Б)

2) cos∠В     В)

Г)

3) tg∠В     Д)

4. У ΔАВС, ∠С=90°, sin∠A=, BC=12см. Знайдіть довжину катета АС.

5. Катет прямокутного трикутника відноситься до гіпотенузи як 5:13. Знайдіть периметр трикутника, якщо його другий катет дорівнює 24см.

6. У трикутнику АВС кут С – тупий. ВС=15см, АВ=20см, ВК – висота трикутника, ВК=12см. Знайти довжину сторони АС.

 

 

 

 

 

 

 

 

Тема 5. Тригонометричні функції гострого кута прямокутного трикутника. Розв’язування прямокутних трикутників.

Варіант 1

 

1. Яка з наведених рівностей неправильна.

А)      Б)          В)         Г)  

2.  У ΔАВС, ∠С=90°, ∠A=60°, АВ=6. Знайдіть АС

А) 3см      Б) 3см   В) 6см    Г) 9см

3. Встановіть відповідність виразами (1-3) і їх значеннями (А-D):

1) sin30°+cos60°    А)

Б)

2) cos30°+tg60°   В)

Г)

3) sin30°cos30°-tg60°    Д)

4. Знайти висоту і основу рівнобічного трикутника, у якому бічні сторони дорівнюють 14см, а кут між ними 120°.

5. Діагональ прямокутника дорівнює 30см, а його сторони відносяться як 3:4. Знайдіть периметр прямокутника.

6. До гіпотенузи прямокутного трикутника проведено висоту й медіану, відстань між основами яких дорівнює 7см. Знайдіть периметр трикутника, якщо висота дорівнює 24см.

 

 

 

 

 

 

 

 

 

Тема 5. Тригонометричні функції гострого кута прямокутного трикутника. Розв’язування прямокутних трикутників.

Варіант 2

 

1. Яка з наведених рівностей неправильна.

А)     Б)          В)  Г)  

2.  У ΔАВС, ∠B=30°, ∠C=90°, DC=20см. Знайдіть АВ.

А) 10см      Б) 40 см   В) см   Г) см

3. Встановіть відповідність виразами (1-3) і їх значеннями (А-D):

1) sin45°- cos45°    А)

Б)

2)cos45°- tg60°   В)

Г)

3) cos30°tg30°+tg45°    Д)

4. Знайти висоту і основу рівнобічного трикутника, у якому бічні сторони дорівнюють 12см, а кут при основі 45°.

5. Діагональ прямокутника дорівнює 26см, а його сторони відносяться як 5:12. Знайдіть периметр прямокутника.

6. До гіпотенузи прямокутного трикутника проведено висоту й медіану, відстань між основами яких дорівнює 7см. Знайдіть периметр трикутника, якщо медіана, проведена до гіпотенузи, дорівнює 25см.

 

 

 

 

 

 

 

 

 

 

Тема 6. Многокутники. Площі многокутників.

Варіант 1

 

1. Який із наведених відрізків не є стороною многокутника АВСDEF.

А)      Б)           В)   Г)  

2.  Чому дорівнює сума кутів семикутника?

А) 1060°      Б) 900°   В) 700°    Г) 1440°

3. Встановіть відповідність трикутником (1-3) його площею (А-D):

1) Трикутник, сторона якого дорівнює 8см,   А)  

а висота, проведена до цієї сторони - 5   Б)  

2)  В)  

   Г)  

3) Рівносторонній трикутник, сторона   Д)  

якого дорівнює 4     

4. Знайти кути опуклого п’ятикутника, якщо вони пропорційні числам 5:6:7:9:9.

5. Паралелограм має таку саму площу, що й квадрат із периметром 32см. Висота паралелограма дорівнює 4см. Знайдіть сторону паралелограма, до якої проведено цю сторону.

6. Радіус кола вписаного в трапецію, дорівнює 4см. Бічні сторони дорівнюють 11см і 14см, а основи відносяться як 2:3. Знайдіть площу трапеції.

 

 

 

 

 

 

 

 

 

 

 

Тема 6. Многокутники. Площі многокутників.

Варіант 2

 

1. Який із наведених відрізків не є стороною многокутника MNKPQL.

А)NM   Б)KP     В)KQ    Г) QL

2.  Чому дорівнює сума кутів восьмикутника?

А) 1060°      Б) 2020°   В) 1080°    Г) 1440°

3. Встановіть відповідність трикутником (1-3) його площею (А-D):

1) Трикутник, сторона якого дорівнює 10см,   А)  

а висота, проведена до цієї сторони - 8   Б)  

2)  В)  

  Г)  

3) Рівносторонній трикутник, сторона   Д)  

якого дорівнює 5     

4. Знайдіть кути опуклого п’ятикутника, якщо вони пропорційні числам 3:5:7:10:11.

5. Паралелограм має таку саму площу, що й квадрат із периметром 24см. Сторона паралелограма дорівнює 12см. Знайдіть висоту, проведену до цієї сторони.

6. Бічні сторони трапеції, дорівнюють 12см і 16см, а основи відносяться як 2:5. Знайти площу трапеції, якщо радіус вписаного кола дорівнює 5см.

 

 

 

 

 

 

 

 

 

 

 

Тема 7. Підсумкова контрольна робота.

Варіант 1

 

1. Яку з приведених властивостей має будь-який паралелограм?

А)діагоналі рівні;

Б)діагоналі взаємно перпендикулярні;

В) діагоналі є бісектрисами кутів; 

Г) діагоналі точкою перетину поділяються навпіл.

2.  Діаметр АВ утворює з хордою ВС кут 50°. Чому дорівнює градусна міра ∠АОС?

А) 50°    Б) 80°  В) 90°   Г) 100°

 

 

3. Установіть відповідність між сторонами (1-3) і його довжиною (А-Д):

1) Висота рівностороннього трикутника,    А)   

зі стороною 9см      Б)  

2)Діагональ квадрата зі стороною 9 см   В)  

3) Діагональ прямокутника зі     Г)  

сторонами 15см і 3     Д)  

4. В опуклому многокутнику три кути рівні і дорівнюють 80°, а сума решти кутів – 300°. Скільки кутів у цьому многокутнику?

5. Основи трапеції відносяться як 2:3, а висота дорівнює 6см. Знайдіть основи трапеції, якщо її площа дорівнює 60.

6. Бісектриса кута трикутника поділяє сторону, до якої проведена, на відрізки 8см і 10см. Знайти дві невідомі сторони трикутника, якщо одна з них на 6см більше другої.

 

 

 

 

 

 

 

 

Тема 7. Підсумкова контрольна робота.

Варіант 2

 

1. Яку з приведених властивостей має будь-який прямокутник?

А)діагоналі взаємно перпендикулярні;

Б)діагоналі є бісектрисами кутів;

В) діагоналі рівні; 

Г) діагональ утворює рівні кути з сусідніми сторонами.

2.  Радіуси АО і СО кола з центром в точці О утворюють кут 60°.Чому дорівнює градусна міра кута між діаметром АВ і хордою ВС?

А) 30°    Б) 60°  В) 120°   Г) 90°

 

 

3. Установіть відповідність між сторонами (1-3) і його довжиною (А-Д):

1) Діагональ квадрата зі стороною 7см    А)   

2)Діагональ прямокутника зі стороною 9 см  Б) 7

сторонами 7см і      В)

3) Сторона ромба, діагональ якого    Г) 2  

дорівнюють 10см і       Д) 3 

4. В опуклому многокутнику чотири кути рівні і дорівнюють 100°, а сума решти кутів – 320°. Скільки кутів у цьому многокутнику?

5. Одна з основ трапеції на 6см менша від другої, а висота дорівнює 8см. Знайти основи трапеції, якщо її площа дорівнює 96.

6. Бісектриса кута трикутника поділяє сторону, до якої проведена, на відрізки 20см і 15см. Знайти дві невідомі сторони трикутника, якщо одна з них на 7см менше другої.