Збірник задач "Геометричний тренажер на клітчастому папері"
Відділ освіти Вінницької районної державної адміністрації
Малокрушлинецька СЗШ І-ІІІ ст.
Збірник задач
«Геометричний тренажер
на клітчастому папері»
2020
Пояснювальна записка
У формуванні ключових компетентностей школярів значну роль відіграє навчання геометрії (формування відповідних предметних компетентностей). Геометрія, як наука, виникла з життєвих потреб людини у глибоку давнину. Змінюючись від практичної до суто дедуктивної, вона перетворилася на феномен загальнолюдської культури. Все, що нас оточує – геометрія. Геометричні знання і вміння, геометрична культура є сьогодні професійно значущими для багатьох сучасних спеціальностей: конструкторів, вчених, дизайнерів і робітників. Серед шкільних предметів математичного циклу геометрія вирізняється вільнодумністю, небажанням підкорятися алгоритмам, а інколи навіть логіці. Вона є потужним засобом розвитку особистості. Геометрія допомагає пізнати оточуючий світ, у якому більшість предметів нагадують різні геометричні фігури. Ми живемо у світі геометрії. Щоб орієнтуватися в ньому, потрібно навчитися розуміти, як він влаштований. Геометрія формує в людини просторову уяву, знайомить з просторовими формами і законами їх сприйняття.
З іншого боку, геометрія має всі можливості для розвитку обох півкуль головного мозку людини, оскільки в ній інтуїтивно зрозумілі факти логічно обґрунтовуються і доводяться.
Це єдиний шкільний предмет, що базується на послідовному доведенні всіх тверджень. А якщо людина розуміється на доведенні, нею неможливо маніпулювати. У навчанні математики роль геометрії не вичерпується її змістом. Наочні інтерпретації допомагають кращому розумінню властивостей геометричних фігур, їх прояву у реальному житті. Також, для успішного формування предметних і ключових компетентностей учням необхідно розв’язати чимало геометричних задач.
Матеріал збірника задач «Геометричний тренажер на клітчастому папері» укладено відповідно до діючих навчальних програм та підручників з математики ( 5-х, 6-х класів) та геометрії ( для 8-х класів).
Ступінь складності задач - різний. Збірник містить задачі за готовими рисунками, що допоможе школяреві краще усвідомити зміст завдань, займаючись самоосвітою та вивільнить на заняттях час учителя.
Збірник задач «Геометричний тренажер на клітчастому папері» сприятиме забезпеченню вчителя математики додатковим матеріалом для наповнення уроків, позакласних заходів та проведення диференціації при формуванні домашніх завдань.
Збірник задач буде корисним для вчителів математики, організаторів математичних олімпіад, турнірів, конкурсів, гурткових і факультативних занять, позакласних заходів з математики. Учням дозволить продуктивніше займатись самоосвітою. Батькам –допоможе тренувати дітей, виконувати посильні завдання та завдання підвищеної складності.
Використання програми GeoGebra дозволить вчителям математики та учням самостійно створювати нові рисунки на клітчастій основі.
Збірник задач «Геометричний тренажер на клітчастому папері» містить три розділи.
Завдання першого розділу спрямовані на повторення та систематизацію знань про площу та периметр многокутників, здобутих у 4-му класі для учнів 5-х та 6-х класів. Зміст задач побудовано на засадах компетентнісного підходу, пов'язаних з процесуальним компонентом навчання математики: переважання самостійної пізнавальної діяльності учнів; можливість створення учнями власного індивідуального освітнього продукту. (Це може бути свій спосіб розв’язання задачі, бачення власного підходу до вирішення проблеми тощо. Він не обов'язково буде оптимальним. Учень повинен мати право на помилку !). Зміст значної частини задач дозволяє відчути «ситуацію успіху» для учнів з низьким рівнем знань, що підвищує їхню активізацію до навчальної діяльності у вивченні геометрії. Усі задачі І розділу збірника взаємозв'язані одна з другою. Розв'язування задач кожного виду допомагає розв'язувати задачі інших видів. Тому вони чергуються в певній системі. Пройшовши тренування розв’язування задач на клітчастій основі, учням легше долати труднощі в алгоритмі розв’язування сюжетних задач на геометричну тематику, тому в І розділі збірника частково пропонуються сюжетні геометричні задачі.
Своєрідним тренажером для формування необхідних рис і якостей та вміння застосовувати знання і поглиблювати їх при навчанні математики є розв’язування нестандартних задач. Стимулюючи до пошуку оригінальних розв’язків при знаходженні площі многокутників у другому розділі збірника задач «Геометричний тренажер на клітчастому папері запропоновано ознайомлення з формулою Піка та представлено задачі на використання методу доповнення до фігури при знаходженні площі многокутників. Опрацювання даного розділу дозволить вивчити формулу австрійського математика Піка для знаходження площі многокутників. Задачі такого типу використовуються в практиці ЗНО сусідніх держав та у різноманітних моніторингових дослідженнях по вивченню якості математичних знань учнів. При розв’язуванні таких вправ на ЗНО, використання даної формули суттєво дозволить учням економити час для розв’язування завдань більшої складності.
Дивергентне мислення учнів формується в процесі їхньої аналітико-синтетичної діяльності такими прийомами, як аналіз через синтез, виконання додаткових побудов, розв’язування задач різними способами , тому в основу представлених завдань у даному збірнику покладено такий важливий механізм формування дивергентного мислення як інтуїція. Сучасні психологічні дослідження свідчать про наявність таких етапів дії інтуїції в людини під час розв’язування задачі (проблеми), як: накопичення в пам’яті образів і абстракцій понять; їх несвідоме перетворення і комбінування з метою вирішення задачі; чітке усвідомлення задачі; її несподіване вирішення. Представлені зразки розв’язування задач, підказки до використання здобутих знань при доведенні (у задачі на доведення) спрямовані на заохочення учнів до інтуїтивних міркувань, оскільки в такий спосіб школярі вчаться будувати гіпотези, прогнозувати результати своєї діяльності, приймати рішення.
Використання різних способів розв’язування задач є корисним для їх порівняння, вироблення в учнів навичок самоконтролю, а головне, формування в них відповідних предметних і ключових компетентностей.
У ІІІ розділі даного збірника розміщенні завдання на розвиток окоміра в частині визначення за клітинками величини кутів; використання в нестандартних ситуаціях теореми Піфагора та розширення можливостей використання співвідношення між сторонами та кутами в прямокутному трикутнику за готовими рисунками.
Самостійне розв’язування школярем задач даного збірника сприятимуть саморозвитку, самоактуалізації учня, дозволяють йому самому шукати й усвідомлювати придатні саме для нього способи вирішення проблем (у тому числі життєвих). Для учня важливо, щоб завдання були доступними, посильними, цікавими і щоб він бачив результат своєї роботи, вчився самостійно контролювати і оцінювати його.
Зміст задач сприятиме формуванню та розвитку у школярів ключових компетентностей, а саме:
- громадянської - здатності критично мислити, аргументувати думку;
-уміння вчитися -здатності міркувати, порівнювати, узагальнювати, спостерігати, самостійно шукати інформацію з різних джерел, набувати індивідуального досвіду самоорганізації, навчальної рефлексії;
-загальнокультурної- здатності застосовувати методи самовиховання, зорієнтовані на систему індивідуальних і загальнолюдських цінностей.
Серед предметних компетентностей, які формуються у процесі роботи за даним збірником є вміння знаходити площу многокутників, в окремих випадках величину вписаних та центральних кутів (із застосуванням окоміру), застосовувати в нестандартних ситуаціях теорему Піфагора , співвідношення між сторонами та кутами в прямокутному трикутнику. Основоположними є природознавча та суспільствознавча компетентності, що виявляються у здатності учнів вирішувати доступні особистісно і соціально значущі практичні проблеми, пов'язані з суспільним життям.
Задачі на клітчастій основі збірника задач «Геометричний тренажер на клітчастому папері» спрямовані на розуміння учнями поняття масштабу, уважне дочитування умов задач ( вправи з додатковим завданням у записі відповідей), на розвиток практичних умінь по визначенню площ многокутників.
Задачі даного збірника чітко формують наступність у вивченні геометрії між початковою та основною школою, тому завдання І-го розділу можуть використовуватись на уроках математики в 4-6 класах та у підготовці до різноманітних моніторингових досліджень, ІІ-го та ІІІ-го розділів на повторення у підготовці до ЗНО.
РОЗДІЛ І. ЗАДАЧІ НА ПОВТОРЕННЯ
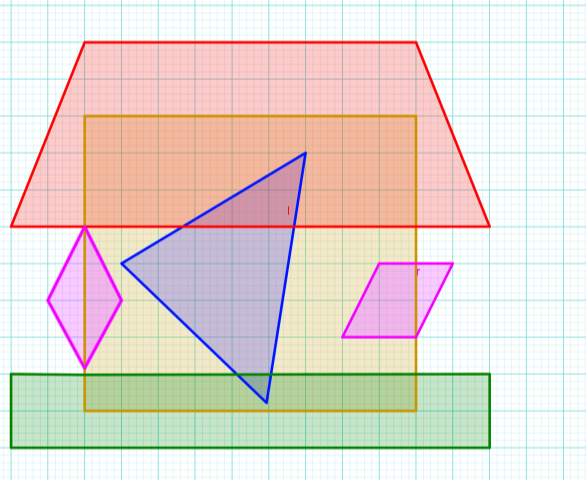
1. Які з наведених многокутників мають однакові периметри?
Малюнок 1
А Б
В Г
Малюнок 2
А Б
В Г
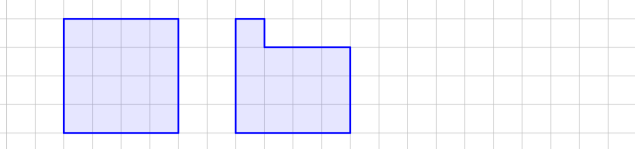
2. Які з наведених многокутників мають однакові площі?
Рисунок 1
А Б
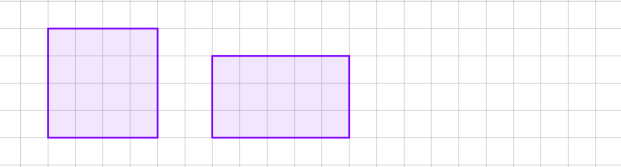
В Г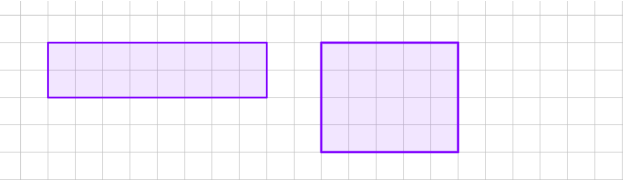 
Рисунок 2
А Б
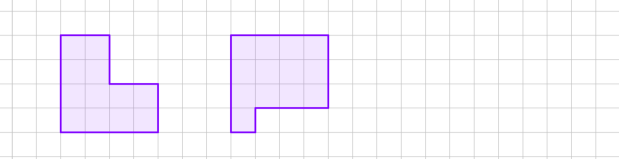
В Г
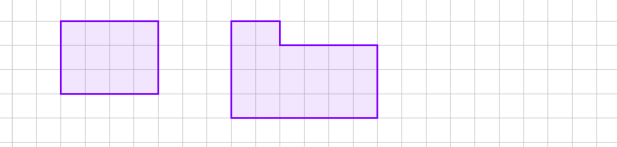
3. Розташуйте фігури у порядку зростання їх площ.
Рисунок 1
А Б В Г
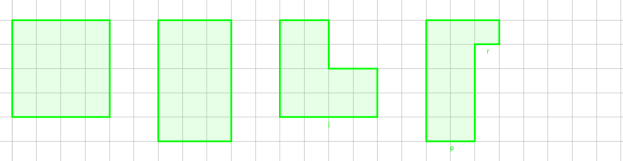
Рисунок 2
А Б В Г
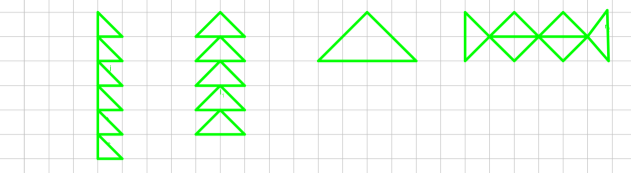
4. Скільки квадратів можна знайти на цих малюнках?
А Б
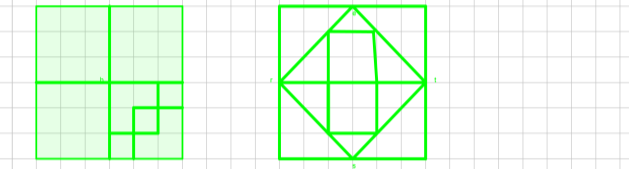
5. Скільки трикутників можна побачити на малюнках? 
А Б
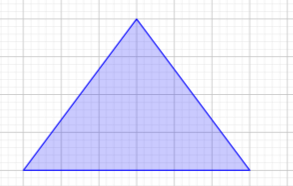
5. Яке найбільше число відрізків потрібно провести в трикутнику, щоб він розділився на три трикутники і один чотирикутник?
А. 2 Б. 3 В. 4 Г. 5
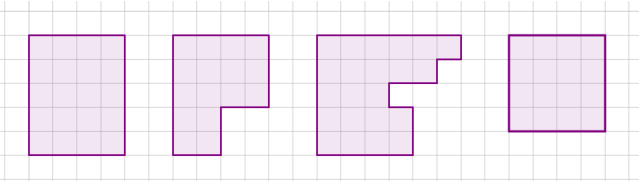
7. Визнач многокутники, які мають однакову площу.
А Б
В Г
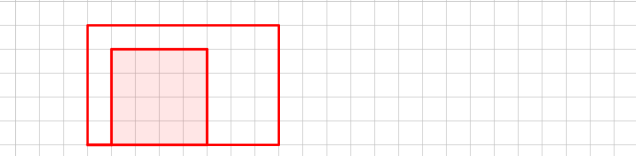
8. У скільки разів площа зафарбованого квадрата менша від загальної площі прямокутника ( довжина 1 клітинки становить 1 см) ?
9. Знайти площу не замальованого многокутника ( довжина 1 клітинки становить 1 см).
10. Знайди площу рамки ( довжина 1 клітинки становить 1 см).
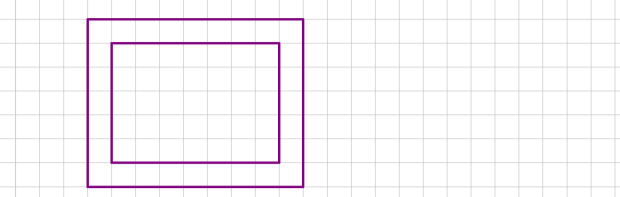
11. Від більшого квадрата відрізали менший квадрат. Знайди площу фігури, яка залишилися
( довжина 1 клітинки становить 1 см).
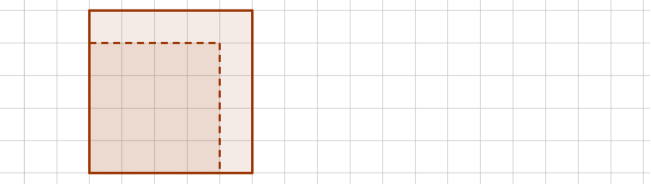
12. Чому дорівнює довжина сторони квадрата, площа якого дорівнює площі даного прямокутника ( довжина 1 клітинки становить 1 см).
13. Скільки квадратів зі стороною 2 см потрібно, щоб покрити даний прямокутник
( довжина 1 клітинки становить 1 см)?
Рисунок 1
А.3 Б. 4 В. 5 Г. 6
Рисунок 2
А. 5 Б.3 В.4 Г.6
Рисунок 3
А. 7 Б.11 В.12 Г.10
14. Чи є серед запропонованих прямокутників з однаковою площею такий, що його можна поділити на 2 рівні квадрати
А
Б
В
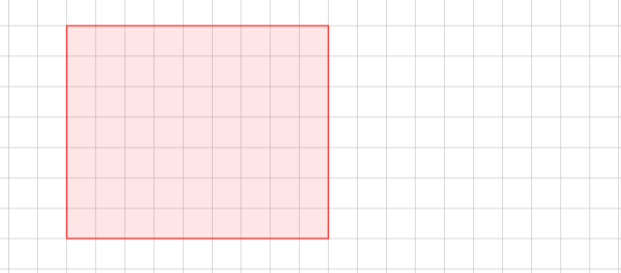
Г
15. Які з наведених фігур мають однакові площі, але різні периметри ( довжина 1 клітинки становить 1 см) ?
А Б В Г
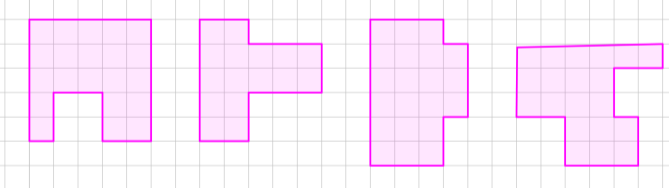
16. Які з наведених фігур мають однакові периметри, але різні площі ( довжина 1 клітинки становить 1 см)?
А Б В Г
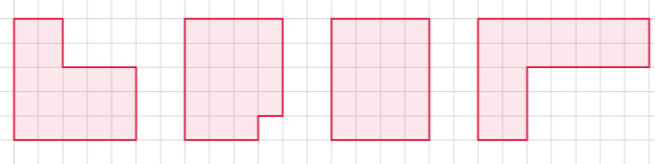
17. Яку площу має прямокутник, периметр якого 24 см? Доведи, що задача має кілька розв’язків і знайди їх.
18. Побудуй прямокутник, площа якого дорівнює 30 см2. Обґрунтуй свою відповідь. Обчисли периметр прямокутника.
19. Довжина футбольного поля 84 м, вона на 22 м більша за його ширину. Знайди площу футбольного поля.
20. На фарбування 1 м 2 підлоги витрачається 250 г фарби. Чи вистачить 4 банки фарби по 3 кг в кожній, щоб пофарбувати підлогу в класній кімнаті довжиною 8 м і шириною 6 м?
21. Чи правильно,що коли периметри прямокутників однакові, то однакові і їх площі? Обґрунтуй свою відповідь.
22. Знайти площі даних прямокутників. Порівняй їх. Знайди їх периметри
( довжина 1 клітинки становить 1 см).
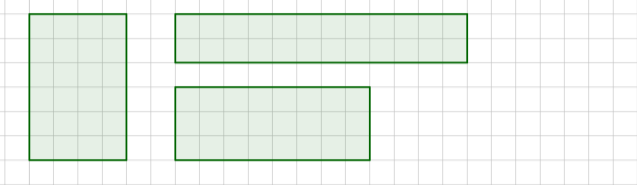
23. Знайти периметри даних прямокутників. Порівняйте їх. Знайти їх площі ( довжина 1 клітинки становить 1 см).
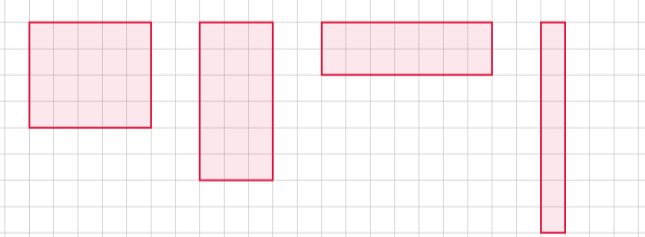
24. Як пов’язані між собою числа: 80, 25, 15, якщо це сторони і периметр прямокутника?
25. Чи правильно, що коли периметри прямокутників однакові, то однакові і їх площі? Обґрунтуй свою відповідь.
26. Накресли квадрат із стороною 5 см. Заштрихуй 1/5 площі даного квадрата. ( довжина 1 клітинки становить 1 см). Скільки квадратних сантиметрів ти заштрихував?
27. Накресли квадрат із стороною 6 см і прямокутник із сторонами 10 см і 2 см. Порівняй їх периметри і площі.
27. Периметр прямокутника 44 см, площа його 72 см2.. Знайди довжину його сторін. Яка відповідь із наведених правильна?
9 см 10 см
24 см 3 см
20 см 2 см
1 см 21 см
4 см 18 см
28. Визнач площу квадрата. Накресли прямокутники, які мають таку ж площу ( довжина 1 клітинки становить 1 см).
29. Площа прямокутника дорівнює 36 см2. Якої довжини можуть бути його сторони?
30. Довжина прямокутного майданчика для ігор 18 м, ширина – 9 м. Скільки потрібно зробити кроків,щоб його обійти, якщо довжина кроку 72 см?
31. В коридорі дитячого садочку, довжина якого 12 м і ширина 5 м, викладали підлогу плитками. Скільки потрібно плиток, якщо площа однієї плитки 1 дм 2?
32. У селі Малі Крушлинці два спортивних майданчика прямокутної форми. Довжина першого майданчика 180 м, а довжина огорожі навколо нього 600 м. Другий майданчик має таку ж площу, але його довжина 270 м. Чому дорівнює ширина другого майданчика ?
33. Ділянка, відведена для побудови стадіону має форму прямокутника, довжина якого 2 км 250 м і ширина 800 м. Скільки спортивних майданчиків можна розбити на п’ятій частині цього стадіону, якщо довжина і ширина кожного майданчика відповідно дорівнюють 80 м і 75 м?
34. Квадратний майданчик для ігор, сторона якого 60 м, посипали піском. Скільки потрібно привезти тачок із піском, якщо на кожні 100 квадратних метрів іде по 3 тачки?
35. Довжина лісової посадки 3 км, ширина у 5 разів менша. За скільки хвилин можна пройти вздовж сторін цієї посадки, якщо йти зі швидкістю 75 м/хв. ?
36. Ширина прямокутника менша від його довжини в 3 рази. Знайди площу і периметр цього прямокутника, якщо його ширина 24 см.
37. Більша сторона прямокутника становить 12 см. Вона більша від меншої сторони на 2 см. Яка площа і який периметр цього прямокутника?
38. Менша сторона прямокутника 18 см. Вона менша від більшої сторони в 3 рази. Яка площа і який периметр цього прямокутника?
39. Більша сторона прямокутника становить 11 дм 5 см. Вона більша від меншої сторони в 5 разів. Яка площа і який периметр цього прямокутника?
40. Менша сторона прямокутника 7 дм 5 см. Вона менша від більшої сторони на 50 мм. Яка площа і який периметр цього прямокутника?
41. Спортивний комплекс має площу 16500 м 2. Футбольне поле займає 2/5 площі всього комплексу. Якою є ширина футбольного поля , якщо його довжина 100 м.
42. Відкритий басейн для плавання, що має довжину 30 м, а ширину на 5 м. меншу, ніж довжина, займає 2/5 площі всієї спортивної споруди. Чому дорівнює площа споруди ?
43. Яку частину зображеної фігури зафарбовано ( довжина 1 клітинки становить 1 см) ? Запиши відповідний дріб.
А Б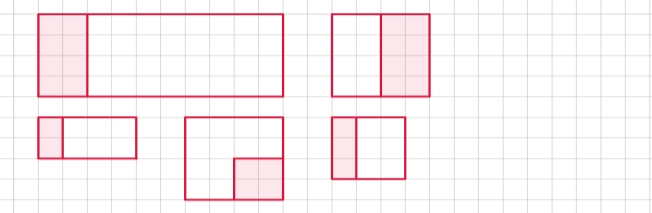 
В Г Д
Відповідь:
1. Рис. 1 ( А, В, Г); рис. 2 (Б, Г)
2. Рис. 1 ( А, В, ); рис. 2 (А, В)
3. Рис. 1 (Г, В, Б, А); рис. 2 ( А, В, Б, Г)
4. А-8; Б-4
5. А-9; Б-8
6. Б-3
7. В; Г
8. У 3 рази
9. 24 см2
10. 28 см2
11. 9 см2
12. 4 см2
13. Рис. 1 (Б); рис. 2 (В); рис. 3 (Г)
14. Б; Г
15. А; В
16. Б; В
17.
|
Довжина |
Ширина |
Площа (S) |
|
5 см |
2 см |
35 см2 |
|
9см |
3 см |
см2 |
|
11 см |
1 см |
см2 |
|
10 см |
2 см |
см2 |
|
… |
… |
… |
18.
|
Довжина |
Ширина |
Периметр (Р) |
|
10 см |
3 см |
26 см |
|
6 см |
5 см |
22 см |
|
15 см |
2 см |
34 см |
|
30 см |
1 см |
62 см |
|
… |
… |
… |
19. 5544м2
20. Вистачить
22.
|
Площа (S) |
Периметр (Р) |
|
24 см 2 |
20 см |
|
24 см 2 |
28 см |
|
24 см 2 |
22 см |
23.
|
Площа (S) |
Периметр (Р) |
|
18 см 2 |
20 см |
|
18 см 2 |
18 см |
|
18 см 2 |
14 см |
|
18 см 2 |
8 см |
27. 4; 18
29.
|
1;36 |
2;18 |
9;4 |
3;12 |
30. 75 кроків
31. 6000 шт.
32. 80 м
33. 60 шт.
34. 108 тачок
35. 96 хв.
36. Р= 192 см; $= 1728 см2
37. Р= 44 см; $= 120 см2
38. Р= 144 см; $= 972 см2
39. Р= 138 см; $= 2645 см2
40. Р= 30 дм 10 10 см; $= 60 дм2
41. 66 м
42. 1875 м2
43.
|
А |
Б |
В |
Г |
Д |
|
1/5 |
1/2 |
1/4 |
1/4 |
1/3 |
РОЗДІЛ ІІ. Теорема Піка
Теорема Піка — класичний результат в комбінаторній геометрії і геометрії чисел.
|
Площа многокутника з цілочисловими вершинами рівна сумі S = M/2 + N - 1 де M - кількість цілочислових точок на межі многокутника. N - кількість цілочислових точок усередині многокутника |
Точка координатної площини називається цілочисловою якщо, обидві її координати цілі числа.
Приклад:
Знайти площу трикутника на заданому малюнку:
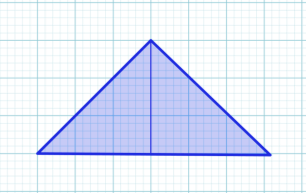
Розв’яжемо дану задачу, використовуючи терему Піка. Визначимо M - кількість цілочислових точок на межі трикутника та N - кількість цілочислових точок усередині трикутника.
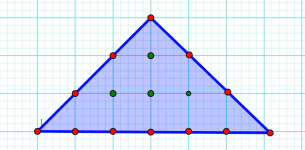
В прикладі на малюнку М = 12 ( точки червоного кольору);
N = 4 ( точки зеленого кольору).
Використовуючи формулу Піка S = M/2 + N - 1 знаходимо площу трикутника:
S = 12/2 + 4 – 1= 9 (квадратних одиниць).
Якщо в умові задачі буде вказано про те, що 1 клітинка дорівнює 1см2 , то
площа вищевказаного трикутника дорівнюватиме S = 9 см2 .
Здійснимо перевірку за відомими геометричними формулами для знаходження площі трикутника (1 клітинка дорівнює 1 см2 ).
S = 1/2 ×6×3 = 9 см2 .
Цікаво знати
|
Площа трикутника з вершинами у вузлах, що не містить вузлів ні всередині, ні на сторонах (окрім вершин), рівна 1/2. Цей факт дає геометричні доказ формули для різниці відповідних дробів ланцюгового дробу . |
Тренувальні вправи:
Обчислити площу многокутників зображених на рисунках 1-11, використовуючи теорему Піка:
Рисунок 1
Відповідь: S = 5/2 + 9 – 1= 10,5 (кв. од. )
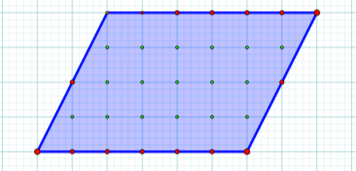Рисунок 2
Відповідь: S = 16/2 + 17 – 1= 24 (кв. од. )
Рисунок 3
Відповідь: S = 4/2 + 12 – 1= 13 (кв. од. )
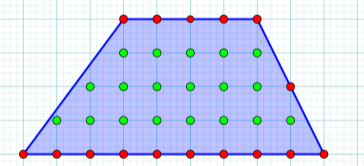Рисунок 4
Відповідь: S = 16/2 + 19 – 1= 26 (кв. од.)
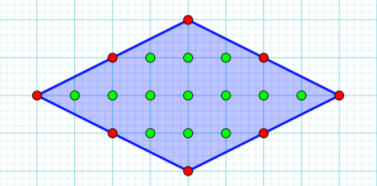Рисунок 5
Відповідь: S = 8/2 + 13 – 1= 16 (кв. од.)
Рисунок 6
Відповідь: S = 2/2 + 16 – 1= 16 (кв. од.)
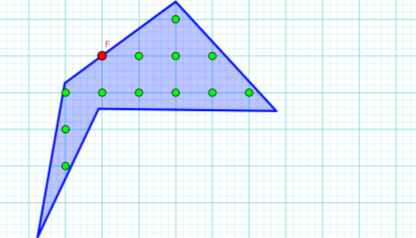Рисунок 7
Відповідь: S = 1/2 + 12 – 1= 11,5 (кв. од.)
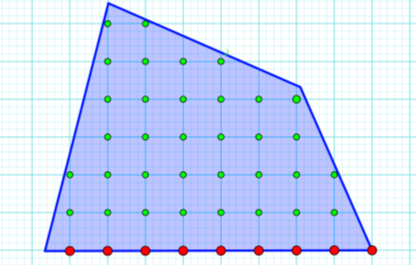Рисунок 8
Відповідь: S = 9/2 + 34 – 1= 37, 5 (кв. од.)
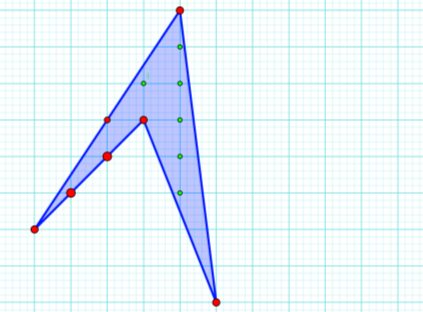Рисунок 9
Відповідь: S = 7/2 + 6 – 1= 8,5 (кв. од.)
Рисунок 10
Відповідь: S = 5/2 + 10 – 1= 11,5 (кв. од.)
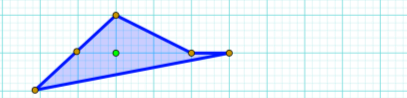Рисунок 11
Відповідь: S = 5/2 + 1 – 1= 2,5 (кв. од.)
Знайти площу многокутників, зображених на рис. 1-14 на клітчатій основі з розміром клітки
1 см × 1 см.
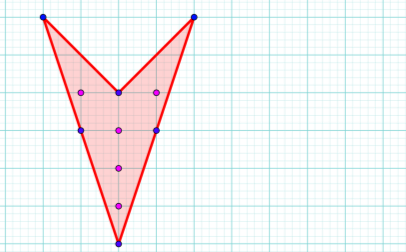Рисунок 1
Відповідь: 7 см2
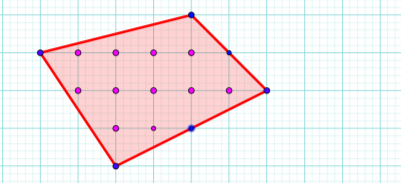Рисунок 2
Відповідь: 13 см2
Рисунок 3
Відповідь: 16 см2
Рисунок 4
Відповідь: 12 см2
Рисунок 5
Відповідь: 1 см2
Рисунок 6
Відповідь: 4 см2
Рисунок 7
Відповідь: 2 см2
Рисунок 8
Відповідь: 1,5 см2
Рисунок 9
Відповідь: 6 см2
Рисунок 10
Відповідь: 20,5 см2
Рисунок 11
Відповідь: 5 см2
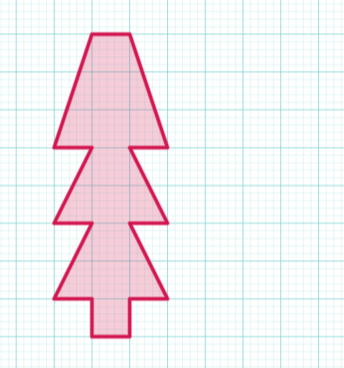Рисунок 12
Відповідь: 15 см2
Рисунок 13
Відповідь: 13 см2
Рисунок 14
Відповідь: 7 см2
Знайти площу п’ятикутника АВСДЕ за допомогою відомих геометричних формул площ многокутників та за формулою Піка (довжина клітинки становить 1 см). Порівняй час витрачений на визначення площі многокутника при використанні різних способів знаходження площі п’ятикутника.
1 спосіб:
S = Sкв - (S Δ АFB + S Δ BJC + S Δ CKD + S Δ DIE + S Δ AGE + S Δ АGHF )
S = 64 – (4+3+6 +5+3+4) =31 см 2
2 спосіб:
S = 6/2 +29 -1= 31 см 2
Відповідь: 31 см 2
Знайти площу чотирикутника АВСД за допомогою відомих геометричних формул площ многокутників та за формулою Піка (довжина клітинки становить 1 см).
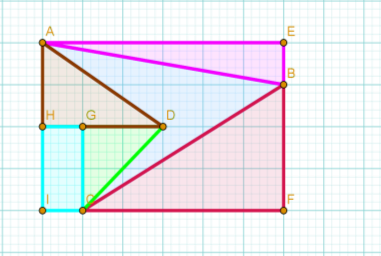
Відповідь: 6,5 см 2
Знайти площу многокутника за допомогою відомих геометричних формул площ многокутників та за формулою Піка (довжина клітинки становить 1 см).
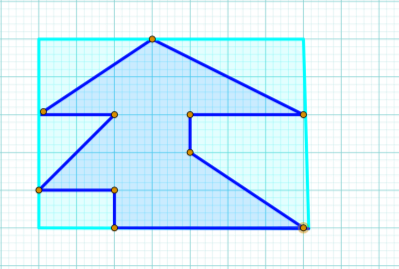
Відповідь: 18 см 2
Знайти площу восьмикутника за допомогою відомих геометричних формул площ многокутників та за формулою Піка (довжина клітинки становить 1 см).
Відповідь: 34 см 2
Знайти відношення площі виділеного восьмикутника до площі квадрата (розмір клітинок
1 см × 1 см).
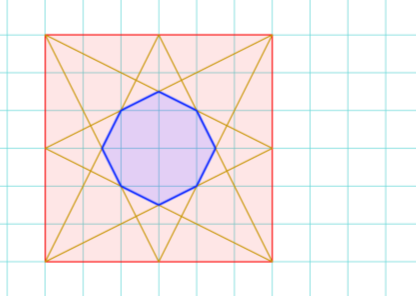
Площа восьмикутника за формулою Піка S = 4/2 + 5 – 1= 6 см2;
Площа квадрата S = 36 см2
Відповідь: 6 см2 / 36 см2 =1/6
Знайти відношення площі виділеного чотирикутника до площі шестикутника (розмір клітинок 1 см × 1 см).
Відповідь: 2 см2 / 26 см2 =1/13
Визначити площу озера, враховуючи те, що розмір клітинок становить 150 м ×150 м
(відповідь запиши в гектарах).
Sф = 44 кв. од.;
Sкл.= 22500 м2
Відповідь: Sоз = 990000 м2 = 99 га
Визначити площу лісової смуги, враховуючи те, що розмір клітинок становить
200 м ×200 м (відповідь запиши в гектарах).
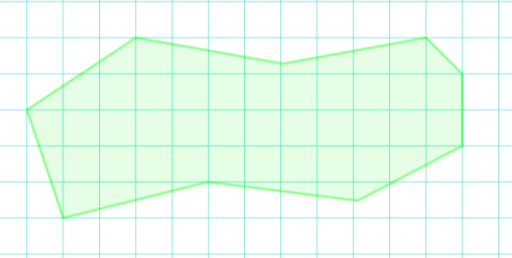
Відповідь: Sоз = 1 740 000 м2 = 174 га
РОЗДІЛ ІІІ.
1. Визначити довжину відрізка АВ зображеного на малюнку (довжина сторони клітинки 1 см):
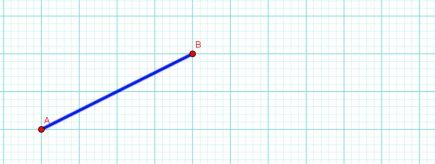
Відповідь: 18 см
2. Вказати номер малюнку на якому tg В =3/4
Рисунок 1
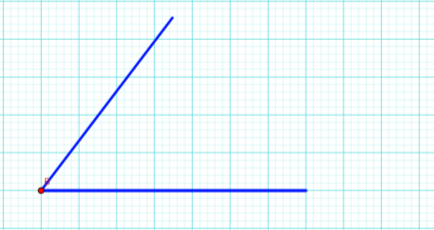
Рисунок 2
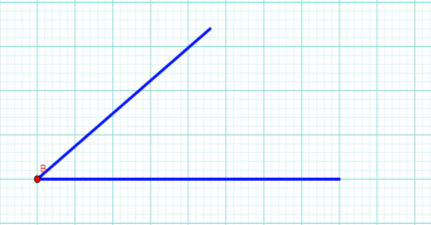
Відповідь: №2
3. Знайти довжину бісектриси кута АВС, враховуючи те, що довжина сторони клітинки дорівнює 2,5 см.
Відповідь: 15 см.
4. Доведіть , що прямі АВ та СD паралельні.
Доведення:
ΔABЕ = ΔСDЕ ( за … ознакою рівності трикутників, так як …=…,
…= …, …=…). З рівності ΔABЕ = ΔСDЕ маємо: ВАЕ= СDЕ, тому
АВ СD (за властивістю паралельних прямих, які перетинаються січною
……………..).
5. Знайти довжину медіани Δ АВС, враховуючи те, що довжина сторони клітинки дорівнює 5 см.
Відповідь: 25 см.
6. Знайти висоту трапеції, якщо довжина сторони клітинки дорівнює 10 см
Відповідь: 25 см
7. На малюнку зображено рівнобедрений трикутник АВС, а СD – висота.
Установити відповідність між значеннями sin А, cos А, tg А, ctg А та їхніми значеннями.
|
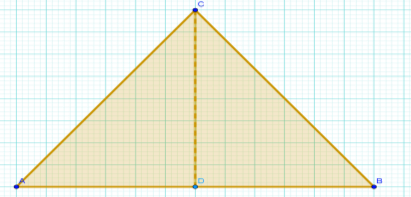
Вирази |
Значення |
|
1. sin А 2. cos А 3. tg А 4. ctg А |
А. 0,75 Б. 0,8 В. 0,6 Г. 0,5 Д. 4/3 |
|
|
А |
Б |
В |
Г |
Д |
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
4 |
|
|
|
|
|
Установити відповідність між значеннями sin АСD, cos АСD, tg АСD,
ctg АСD та їхніми значеннями.
|
|
А |
Б |
В |
Г |
Д |
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
Вирази |
Значення |
|
1. sin АСD 2. cos АСD 3. tg АСD 4. ctg АСD |
А. 3/5 Б. 4/3 В. 0,6 Г. 0,8 Д. 0,75 |
8. Визначити за малюнком значення sin А. Відповідь записати у вигляді звичайного дробу
(чисельник та знаменник дробу - натуральні числа).
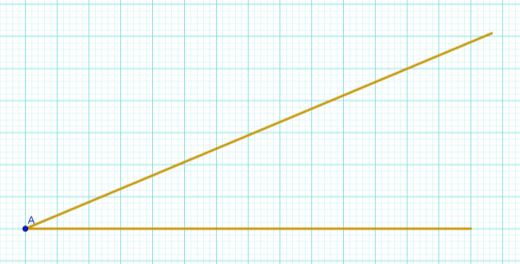
Відповідь: sin А = 5/13
9. Знайти величину СВD ( відповідь надати в градусах).
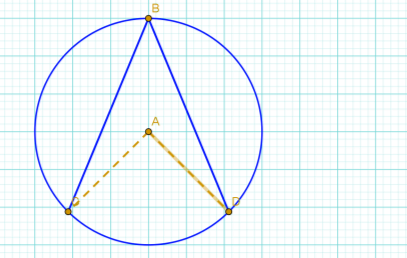
Відповідь: СВD =450
10. Знайти величину ЕСD ( відповідь надати в градусах).
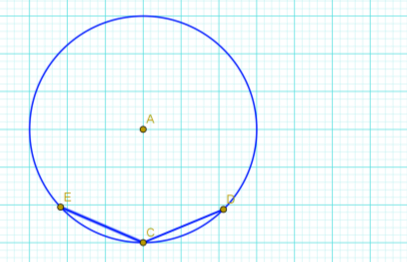
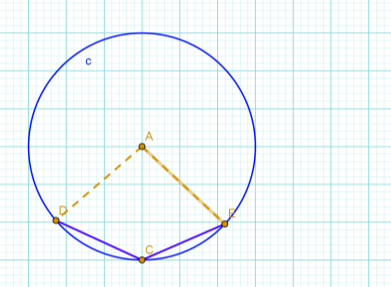
Відповідь: ЕСD = 1350
11. Знайти величину ЕСD ( відповідь надати в градусах).
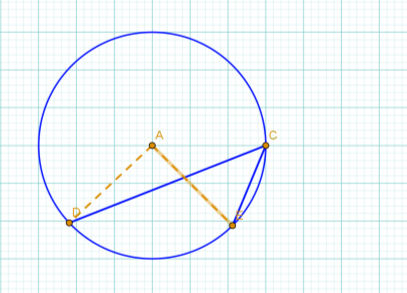
Відповідь: ЕСD = 450
12. Знайти градусну величину дуги DЕ на яку опирається DСЕ .
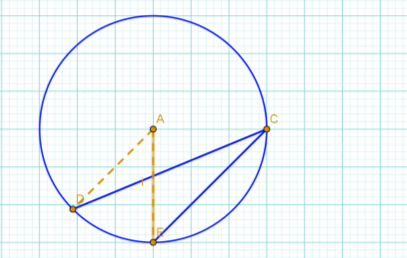
Відповідь: 450
13. Знайти градусну величину дуги ВD на яку опирається ВСD .
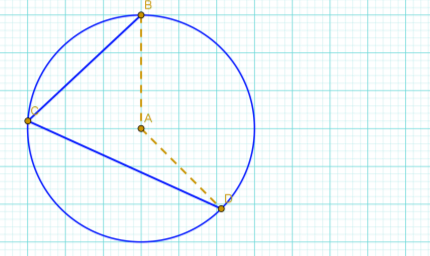
Відповідь: 1350
14. Знайти радіус кола, описаного навколо прямокутного Δ DСЕ (довжина сторони клітинки дорівнює 2,5 см ) .
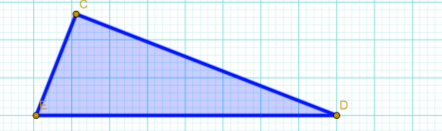
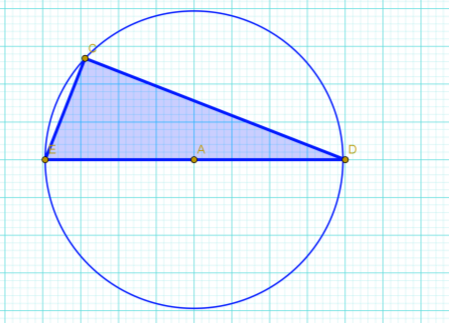
Відповідь: 10 см.
15. Знайти радіус кола вписаного в квадрат АВСD (довжина сторони клітинки дорівнює
5 см ). Результат домножити на 5 .
Відповідь: 10 2 см.
Література:
1. Глобін О.І. Компетентнісно орієнтована методика навчання математики в основній школі: Метод. посібник / Глобін О.І., Бурда М.І., Васильєва Д.В.,. Волошена В.В, Вашуленко О.П., Мацько Н.Д., Хмара Т.М. — К.: Педагогічна думка, 2015. – 245с.
2. Прасолов В. В. Задачи по планіметрії. — М.: МЦНМО, 2001. — 584 с.
3. Геометрія на клітчастій бумазі. Малый МЕХмат МГУ. [Електронний ресурс] http://mmmf.msu.ru/archive/20082009/KanunnikovKuznetsov/2.html
4. Ігнатьєв Е. И. В царстві смекалки / М.: Наука, 1982.
5. Прасолов В. В. Задачі з планіметрії./ М.: МЦНМО, 2000.
6. Екимова М. А. Задачі на розріз /Екимова М. А., Кукин Г. П. М.: МЦНМО, 2002. [Електронний ресурс]: http://www.math.ru/lib/files/pdf/kukin.pdf
7. І.М. Кривошея Задачі міжнародних математичних чемпіонатів. Кривошея І.М., Збожинстька Т.С. –Вінниця, «Поділля-2000», 2007-120 с.
8. Аміршадян А.А. Математичний конкурс «Золотий ключик»/ АміршадянА.А. та інші –Львів.Каменяр, 2004 -100 с.
9. Добосевич А.С. 10 років разом . Міжнародний математичний конкурс «Кенгуру» 1997-2006/
Добосевич А.С. та інші .-Львів. Каменяр,2006.-234 с.
10. Будна Н. Збірник задач і текстових завдань з математики: 4 клас /
Навчальна книга - Богдан 2016 р. 192 ст.
11. Васютенко В. 200 задач з математики. 4 клас Розв’язуємо задачі.Торсінг Плюс 2015 р.
32 ст.
12. Гребенькова Л. О. Розв`язую задачі. 4 клас. Зошит-помічник. Серия «За партою», вид-авництво
13. Карнаух П. Цікаві завдання з математики: 4 кл. / П. Карнаух. – Тернопіль: Підручники і посібники, 2007. – 32 с. 25.
14. Математика – це справді цікаво. М. Беденко 1- 4 класи. 2009 р. Тернопіль, “Богдан”
15. Лихва А.В . Логіка 2-4 класи. Розробки занять / укл. Лихва А.В., Фастова Н.В. – 3- тє вид. – Х.: Вид. група “Основа”, 2010. – 268с.
-
-
-
Чудовий матеріал для розвитку логічного мислення учнів.
про публікацію авторської розробки
Додати розробку