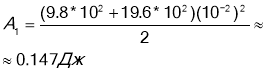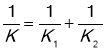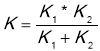3.  
4.  

 

МІНІСТЕРСТВО  ОСВІТИ  І  НАУКИ  УКРАЇНИ

КАМ’ЯНСЬКЕ ВИЩЕ ПРОФЕСІЙНЕ

УЧИЛИЩЕ

 

 

 

 

ЗБІРНИК

 

"МЕТОДИЧНІ РЕКОМЕНДАЦІЇ

ПО РОЗВ'ЯЗУВАННЮ ЗАДАЧ

З ФІЗИКИ"

 

 

 

 

 

 

 

 

 

 

 

КАМ’ЯНСЬКЕ

2021

ВСТУП

 

Знання фізики - це насамперед розуміння фізичних явищ, законів і величин, що їх характеризують. Тому розв'язування учнями задач під час вивчення фізики має надзвичайно велике значення. Відомо, що чим більше учні розв'язують задач, тим швидше вони поглиблюють і розширюють свої знання про фізичні величини, явища, закони, теорії і міцніше засвоюють навчальний матеріал.

Навчання - це не лише запам'ятовування формулювань законів та їх математичних формул, а й свідоме розуміння учнями фізичної суті цих законів, уміння використовувати їх практично.

Ефективність вивчення курсу фізики, очевидно, буде найбільшою лише тоді, коли учні виявлятимуть максимум ініціативи й самостійності до будь - якого виду роботи, з вивчення курсу фізики і особливо під час розв'язування фізичних задач.

Щоб забезпечити самостійність та уникнути формалізму під час розв'язування задач, треба частіше впроваджувати індивідуальні завдання як безпосередньо на уроці, так і вдома.

Складаючи систему фізичних задач, слід ураховувати структурну особливість фізичної науки і саму структуру предмета навчання. Ефективність навчання розв'язування задач визначається, в першу чергу, тими завданнями, які ставляться перед розв'язуванням кожної задачі в системі всієї навчальної роботи. Виходячи зі сказаного вище і слід складати систему задач.

Підібрані задачі мають відповідати таким дидактичним вимогам, основою яких є поступове ускладнення зв'язків між величинами й поняттями, що характеризують процес або явище, описуване в задачі.

Під час вивчення окремого питання спочатку розв'язують якісні задачі, потім - розрахункові, експериментальні, графічні, поступово збільшують кількість зв'язків між величинами і поняттями. На заключному етапі розв'язують комбіновані задачі, які включають у себе значне коло питань, що вимагають знань раніше вивченого матеріалу. Комбіновані задачі допомагають встановити місце матеріалу, що розглядається, у системі фізичних знань.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ЗМІСТ

ВСТУП           3

РОЗДІЛ І МЕХАНІКА         5

1. Кінематика                    5

Основні закони і поняття, формули     5

Алгоритм розв'язання задач      7

Прилади розв'язання задач      8

Задачі                           13

 

2. Динаміка                                               17

Основні закони і поняття, формули     17

Алгоритм розв'язання задач      19

Приклади розв'язання задач      19

Задачі                             25

 

3. Закони збереження                                       26

Основні закони і поняття, формули     26

Алгоритм розв'язання задач      29

Прилади розв'язання задач      30

Задачі                             36

 

РОЗДІЛ ІІ МОЛЕКУЛЯРНА ФІЗИКА. ТЕРМОДІНАМІКА  43

Основні закони і поняття, формули     43

Алгоритм розв'язання задач      47

Прилади розв'язання задач      49

Задачі                             57

 

ЛІТЕРАТУРА                                                                                              60

 

РОЗДІЛ І. МЕХАНІКА

 

Кінематика

 

Основні поняття, закони і формули

 

Механіка - частина механіки, яка вивчає закони механічної взаємодії тіл і явища механічного руху Механічний рух - зміна положення рухомого тіла відносно інших тіл, які називають тілами відліку. Кінематика - частина механіки, яки вивчає геометричні і математичні характеристики руху без дослідження фізичних причин руху і його зміни.

Сукупність тіла відліку, зв'язаної з ним системи координат і приладів для вимірювання інтервалу часу. утворює систему відліку в механіці.

Матеріальна точка - модель протяжного тіла, яку застосовують у випадку поступального руху цього тіла, нехтуючи його дійсними розмірами і формою.

Траєкторія - лінія, яку описує у просторі рухома точка в процесі механічного руху. Розрізняють рухи прямолінійні і криволінійні. Окремий випадок останніх - рух по колу.

Шлях S - скалярна характеристика механічного руху. Він вимірюється відстанню, пройденого точкою за відповідальний час уздовж траєкторії. Перемі­щення точки - г-вектор, проведений з початкового положення точки у кінцеве (S)=м.

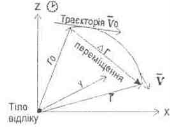Положення матеріальної точки можна задати радіус - вектором г(і), або його проекціями на коорди­нати віссі. Радіус - вектор - це вектор, проведений з початку координат у положення матеріальної І точки в даний момент часу 1 її руху. Кінець г описує траєкторію.

Швидкість V або миттєва швидкість матеріальної точки - вектор ,що визначається значенням похідної за часом від радіуса - вектора.

  

Швидкість у кожній точці траєкторії направлена по дотичній до траєкторії точки і зображується відповідним вектором ,а якщо під час руху точки її швидкість не змінюється ні за модулем ні за напрямком ,то такий рух е прямолінійний рівномірний .

       (2)

Коли протягом часу t,по довільній траєкторії був пройдений шлях 8, то можна визначити середню швидкість . Це скаляр

(3)

Якщо точка бере участь у двох незалежних прямолінійних і рівномірних рухах із швидкостями то швидкість результуючого руху V визначається за формулою: . Модуль результуючої швидкості дорівнює:

  , де

Якщо вектор швидкості змінюється з часом , головною характеристикою цих змін є прискорення а. Це похідна за часом від швидкості або друга похідна за часом від радіуса - вектора r точки.

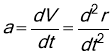  (6) 

Якщо рух відбувається по прямій і модуль прискорення сталий, його називають рівноприскореним прямолінійним рухом.

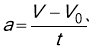 (7)  (8) 

Пройдений за час шлях дорівнює :

Якщо виключити час руху, то:

Якщо кінцева швидкість менша від початкової, рух називають рівносповільненим(а 0).

Тоді: (11)  

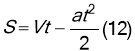
Окремим випадком прискореного прямолінійного руху є вільне падіння. Приско­рення вільного падіння позначають g.

У випадку вільного падіння використовують формули (8)-(13) виконуючи заміни а на g; S на h. У кінці швидкість дорівнює "0"

При вивчені криволінійного руху вектор при­скорення розкладають на дотичній а і нормалі а_n до траєкторії

 .

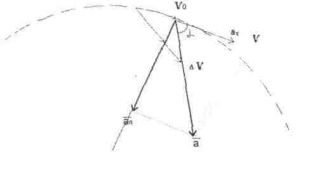
- кут між напрямком , прискорення дотичній до траєкторії.

Дотичне прискорення напрямлено по швидкості, або протилежно їй.

Воно характеризує зміну модуля швидкості.

Нормальне прискорення перпендикулярно до швидкості і характеризує зміну швид­кості за напрямком.

Рух по колу - це найпростіший випадок криволінійного руху.

 

 

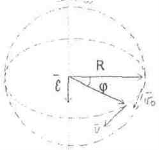
Т- період обертання

N- кількість обертів

n- частота обертання.

- кутова швидкість

- кут повороту

; ; 

, якщо тіло зробило N обертів. , (нормальне прискорення). При обертальному русі тіла всі його точки рухаються по колу, центри яких знаходяться на одній прямій, яка називається віссю обертання. ; ; ; .

- кутове прискорення. Це похідна за часом від кутової швидкості.

 

Якщо тіло обертається з сталим кутовим прискоренням, то:

    

(27)   - дотичне прискорення

[]=рад/с; [] - рад/с² ;[] - об/хв ;1об=2рад 1хв=60с, об/хв=-2/60 рад/с. Для того, щоб розв'язати задачу з кінематики, треба знати всі закони руху.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Алгоритм розв'язання задач

 

1.Спочатку треба уважно прочитати умову задачі і зробити схематичний малюнок, на якому вказати систему відліку і траєкторію руху. Потім вказати відрізку шляху, швидкості і часу руху тіла. Потім встановити зв'язок між усіма вели­чинами, яки вказані на малюнку і записати у виді рівняння.

2.Якщо рухається декілька тіл і треба знайти їх швидкість відносно один одного, то найкраще систему координат зв'язати з одним з цих тіл. Тоді тіло відліку вважаємо нерухомим і визначаємо швидкість і переміщення відносно цього тіла. Потім скла­даємо рівняння руху і записуємо додаткові формули.

3. Якщо тіло кинуто вертикально у гору зі швидкістю V, то час його піднімання і макси­мальна висота визначаються:

Крім того, час падіння цього тіла в точку дорівнює часу піднімання (), а швидкість падіння дорівнює початкової швидкості кидання ().

4. Якщо тіло кинуто під кутом до горизонту, його рух розглядають як результат одно часового прямолінійного руху вздовж вісі х та у. Треба спочатку знайти проекції вектора швидкості на ці вісі і скласти рівняння для кожного з напрямків. Якщо опору немає , час руху по вісі х дорівнює часу руху по вісі у і траєкторія руху - парабола. Вздовж вісі х рух рівномірний. Вздовж вісі у рух рівносповільнений поки тіло не зупиниться , а далі рух рівноприскоренний.

 

        

 

 

 

 

 

 

 

 

 

 

 

 

 

 

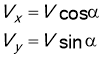
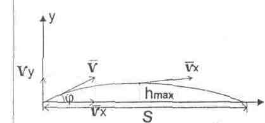
Приклади розв'язування задач

 

Приклад 1.

Першу половину свого шляху автомобіль рухався зі швидкістю V=80км/год, а другу половину шляху - зі швидкістю V=40 км/год. Яка середня швидкість руху автомо­біля ?

Дано:

На кожному відрізку шляху тіло рухається рівномірно

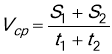;  т.к.

Час руху тіла знаходимо з закону рівномірного руху

 

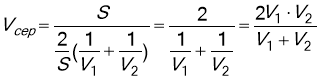
Відповідь: середня швидкість руху автомобіля 53,3 км/год

 

Приклад2.

Два велосипедиста рухаються назустріч один одному. Перший має швидкість 18 км і рухається рівносповільненно з прискоренням 20 м/с². Другий має швидкість 5,4м/с. Через який час вони зустрінуться ? Яке переміщення зроби кожний з них, якщо на початок руху відстань між ними 130м?

 

 

Дано:   СІ

 

 

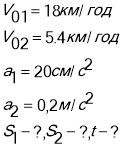
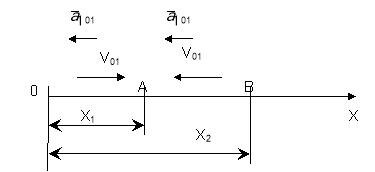Вісь х співпадає з напрямком руху першого тіла, а початок координат - з точкою "О", де знаходилось тіло на початку свого руху (t=0) (х=0). Тоді друге тіло знаходилось у точці В і його координата почат­кова =130м.Запишемо рівняння руху цих тіл.

  ;  

, так як вони рухалися одночасно. У момент зустрічі у точці А тіла мають однакову координату:

; 

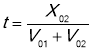Відповідь: велосипедист зустрівся через 20с. перший проїде 60м, а другий - 70м.

 

Приклад 3

Тіло вільно падає з висоти 490 м. Визначити переміщення тіла в останню секунду падіння. Вісь координат зв'яжемо з тілом, яке знаходиться на висоті h і додатковий напрям вісі У виберемо у низ.

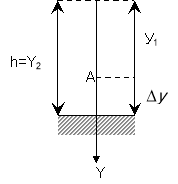 Дано

 

 

 

 

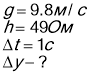
коли тіло впаде на землю.

Коли тіло буде у точці А , його координата

так як його час руху

 

тоді ;

час t2 знаходимо з рівняння (1)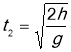

отже: ;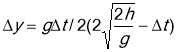

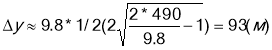
Відповідь: в останню секунду тіло пройде 93м.

 

 

 

 

 

 

 

 

Приклад 4.

Човен рухається перпендикулярно до берега зі швидкістю 2мс. Швидкість течії 5 км/год. Під яким кутом до віссі "У" і з якою швидкістю відносно поверхні води човен тримає курс? Розглядаємо рух човна відносно берега .Тоді швидкість човна , де - швидкість течії води, - швидкість човна відносно води . Так як по умові задачі, то

Дано:  СІ

 

 

 

 

 

; ;   

Відповідь: човен рухається зі швидкістю 2,4 м/с.

 

Приклад 5

Літак летить горизонтально зі швидкістю 360км/год на висоті 490м. Коли він пролітає над точкою А, з нього кидають вантаж на який відстань від точці А він впаде на землю?

 Дано:

 

 

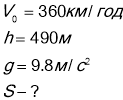
Початок координат зв'яжемо з точкою А .Одночасово тіло приймає участь у двох рухах рівномірний і прямолінійний рух вздовж .вісі Х і вільне падіння з початковою швидкістю вздовж вісі У.

 під час падіння у=0;. Тоді

   ; 

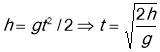
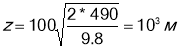
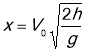Відповідь:

 

 

 

Приклад 6.

Тіло кинуто зі швидкістю 50 м/с під кутом 35⁰ до горизонту. Визначити максимальну висоту підйому і далекість польоту .

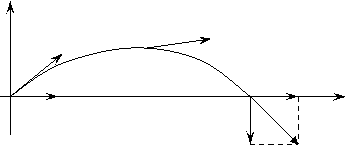Дано:

 

 

 

 

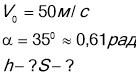
Початок системи відліку зв'яжемо з моментом, коли тіло вилітає. Запишемо рівняння руху тіла

 

Швидкість тіла вздовж вісі У змінюється по закону (3) Для точки А  час.

Тоді рівняння (3) має вигляд :

застосовуючи рівняння (2) до точки А маємо: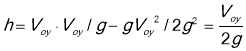

Враховуючи, що сполучаємо

Залишимо рівняння (2)до точки В, коли тіло падає на землю:

   

  де - це час руху тіла до точки В.

(5); ;  

 

Відповідь: максимальна висота польоту 41,3м,а далекість польоту 240м.

 

Приклад 7

Тіло рухається вздовж вісі Х по закону . Знайти середню швидкість тіла і прискорення за час 1-4с. Побудувати графіки переміщення .швидкості та прискорення.

Дано:

 

 

   

 

 

 

 

 

 

 

 

 

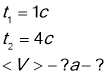
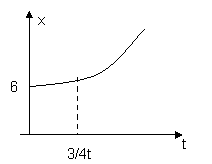
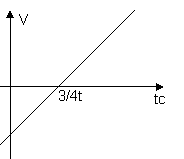
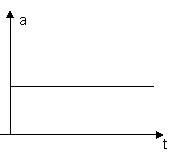
Приклад 8.

Колесо під час обертання має початкову частоту 5с^-1 .Підчас гальмування за 1 хвилину його частота зменшилася до 3с^-1 . Знайти кутове прискорення колеса і кількість обертів ,які воно зробило .

Дано:

  

 

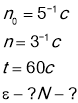
Отже, рівняння (2) можно записати:

Підставимо(З) у (1) тоді   

Відповідь: кутове прискорення колеса 0,21рад/с² і колесо зробило 240 обертів

 

 

 

 

Приклад 9  

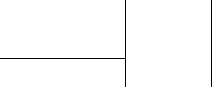
Колесо обертається по закону . Знайти кутову швидкість, лінійну швидкість і повне прискорення точек, якщо вони знаходяться на ободі колеса у кінці першої секунди обертання . Радіус колеса 20 см.

 

 

 

 

Дано:  СІ   

   

 

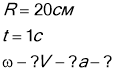
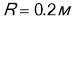
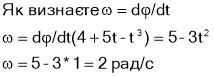
Лінійна швидкість ; 

  

Повне прискорення    Тоді

Відповідь:

 

Задачі

 

1. Першу половину часу свого руху автомобіль рухався зі швидкістю V₁=80 км/год, а другу половину часу - зі швидкістю V₂=40 км/год. Яка середня швидкість V руху автомобіля?

 

2. Пароплав іде по річці від пункту А до пункту В зі швидкістю V₁=10км/год, а назад - зі швидкістю V₂=16 км/год. Знайти середню швидкість V пароплаву та швидкість u течії ріки.

 

3. Знайти швидкість V відносно берега ріки: а) човна, що іде за течією;

б) човна, що іде проти течії;  в) човна, що іде під кутом =90° до течії. Швидкість течії ріки u=1,00 м/с, швидкість човна відносно води V₀=2,00 м/с.

 

4. Човен рухається перпендикулярно до берега зі швидкістю V=7,2 км/год. Течія віднесе його на відстань l=150 м униз по річці. Знайти швидкість й течії ріки і час t, витрачений на переправу через ріку. Ширина ріки L=500 м.

 

5. Камінь кинули вертикально угору на висоту h₀=10м. Через який час t він упаде на землю? На яку висоту h підніметься камінь, якщо початкову швидкість каменю збільшити вдвічі?

 

6. З аеростату, що находиться на висоті h=300м, упав камінь. Через який час t камінь досягне землі, якщо: а) аеростат піднімається зі швидкістю V=5м/с; б) аеростат опускається зі швидкістю V=5м/с; в) аеростат нерухомий.

 

7. Тіло падає з висоти h=19,6м з початковою швидкістю V₀=0. Який шлях пройде тіло за першу і останню 0,1 с свого руху?

 

8. Тіло падає з висоти h=19.6м з початковою швидкістю V₀=0. За який час тіло пройде перший і останній їм свого шляху?

 

9. Поїзд рухається рівносповільнено, у бігу часу t=1,00 хвил. зменшує свою швидкість від V₁=40,0 км/год до V₂=28,0 км/год. Знайти прискорення а поїзду і відстань S, пройдене ним за час гальмування.

 

10. Поїзд рухається рівносповільнено, маючи початкову швидкість V₀=54,0 км/год і прискорення а= -0,50 м/с² .Через який час t і на якій відстані S від початку гальмування поїзд зупиниться.

 

11. Тіло 1 рухається рівноприскорено, маючи початкову швидкість V₁₀ і прискорення а₁ . Одночасно з тілом 1 починає рухатися рівносповільнено тіло 2, маючи початкову швидкість V₂₀ і прискорення а₂. Через який час t після початку руху обидва тіла будуть мати однакову швидкість?

 

12. Залежність пройденого тілом шляху S від часу t дається рівнянням , де А=3м, В=2 м/с і С=1 м/с² . Знайти прискорення а і середню швидкість <V> тіла за першу, другу і третю секунди його руху.

 

13. Залежність пройденого тілом шляху S від часу t дається рівнянням , де С=0,14 м/с² і В=0,01 м/с³ . Через який час t після початку руху тіло буде мати прискорення а=1 м/с² ? Знайти середнє прискорення а тіла за цей проміжок часу?

 

14. З вежі висотою h=25,0 м горизонтально кинуто камінь з швидкістю V_X=15,0 м/с. Який час t камінь буде в русі? На якій відстані l від основи вежі він упаде на землю? З якою швидкістю v він упаде на землю? Який кут складе траєкторія каменя з горизонтом в точці його падіння на землю?

 

15. Камінь кинутий горизонтально, упав на землю через час t=0,500 с на відстані l=5,00 по горизонталі від місця кидання. З якої висоти її кинуто камінь? З якою швидкістю V_X  його кинуто? З якою швидкістю V він впаде на землю? Який кут складе траєкторія каменя з горизонтом в точці його падіння на землю?

 

16. М'яч кинутий з швидкістю V₀=10,00 м/c під кутом =40° до горизонту. На яку висоту її підніметься м'яч? На якій відстані l від місця кидання він упаде на землю? Який час t камінь буде в русі?

 

17. Тіло кинуто з кинуто з швидкістю V₀=14,70 м/с . під кутом =30° до горизонту. Найти нормальне а_n та тангенціальне а_τ прискорення тіла через час t=1,25с після початку руху.

 

18. Найти радіус R обертаючогося колеса, якщо відомо що лінійна швидкість V₁ точки, яка, лежить на ободі, в 2,5 рази більша лінійної швидкості V₂ точки, яка лежить на відстані r=5,00см ближче до осі колеса.

 

19. Колесо обертаючись рівноприскорено, достигло кутової швидкості ω=20,0 рад/с. через N=10o6 після початку обертання. Найти кутове прискорення а колеса.

 

20. Колесо, обертаючись рівноприскорено, за час t=60,0с з початку обертання набуло частоти n=720об/хв. Найти кутове прискорення α колеса і число обертів N колеса за цей час.

 

21. Колесо, обертаючись рівносповільнено, за час t=60,0с зменшило свою частоту з n₁=300об/хв. до n₂=180об/хв. Найти кутове прискорення α колеса і число обертів N колеса за цей час.

 

22. Вентилятор обертається з частотою n=900об/хв. Після вимикання, вентилятор, обертаючись рівносповільнено, зробив до зупинки N=7506. Який час t пройшов з моменту вимикання вентилятора до повної його зупинки?

 

23. Вал обертається з частотою n=180об/хв. З деякого моменту вал почав обертатись рівносповільнено з кутовим прискоренням α=3рад/с² .Через який час t вал зупиниться. Найти число обертів N вала до зупинки?

 

24. Tочка рухається по колу радіусом R=10,0см з постійним тангенціальним а_τ прискоренням. Найти нормальне а_n прискорення точки через час t=20с після початку руху, якщо відомо що до кінця п'ятого оберту після початку руху лінійна швидкість точки V=10,0см/с.

 

25. Колесо обертається з кутовим прискоренням α=2,00рад/с². Через час t=0,500с після початку руху повне прискорення колеса а=13,6см/с² . Найти радіус R. колеса.

 

26. Колесо радіусом R=0,100м обертається так, що залежність кута повороту радіуса колеса від часу дається рівнянням , де , В=2,00рад/с і С==1,00рад/с³ для точок які знаходяться на ободі колеса, найти через час t=2,00с після початку руху: а) кутову швидкість ω; б) лінійну швидкість V; в) кутове прискорення ε; д) нормальне а_n, і тангенціальне а_τ прискорення.

Динаміка

 

Основні поняття, закони і формули

 

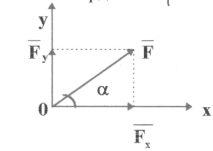
Динаміка - розділ механіки, що вивчає рух і взаємодію механічних об'єктів, зміни характеристик їх руху під дією сили .Сила F - це одне із найважливіших понять динаміки . Сила - міра взаємодії тіл під час якої тіла деформуються, або набувають прискорення. Сила - векторна величина. Вона характеризується числовим значенням, напрямком дії і точкою прикладання .

Найбільш універсальною силою є сила гравітаційної взаємодії об'єктів природи.

 (1)

G - гравітаційна стала.

Прискорення вільного падіння "g" створюється притягання тіла до землі.

Цю силу прийнято називати силою тяжіння землі . Вона прикладена до "центра тяжіння тіла" , напрямлена до центра Землі, а модуль її завжди дорівнює mg.

Вага тіла Р - це сила , з якою воно діє на нитку підвісу ,або горизонтальну опору. Отже вага тіла прикладена до опори ,або до підвісу і напрямлена до центру Землі. Модуль ваги Р = mg лише тоді, коли тіло неру­хоме або рухається прямолінійно і рівномірно. Сила ваги рівна і протилежна силі реакції горизонтальної опори N ,або натягу підвісу - Т.

 

 

 

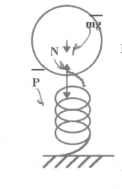
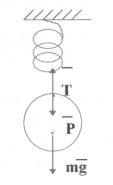Якщо тіло рухається з прискоренням , його вага змінюється.

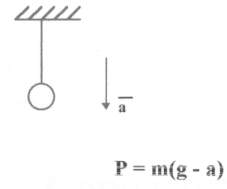
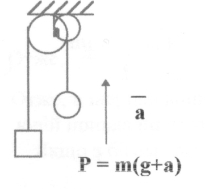Важливим випадком реакції опори є пружна сила . Вона виникає під час деформації пружини. Гук експериментально показав , що модуль цієї сили пропор­ційний величині зміщення кінця пружини.

К - характеристика жорсткості даної пружини .Знак "-" показує, що напрям . протилежний напрямок зміщення пружини .

Якщо два тіла дотикаються у певній точці А , то сукупність великої кількості сил взаємодії їх молекул можна замінити результуючою силою Р дії тіла 2 на тіла 1. Невизначеність у більшості випадків напряму цієї сили примусила фізиків виділити дві її складові реакцією опори N і силу тертя Р пр кути між якими завжди 90⁰.

Вектор реакції опори N завжди напрямлений перпендикулярно до дотичної площини у точці дотику. Реакція опори тим більше, чим дужче деформується тіла у точці дотику.

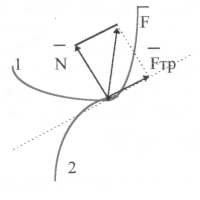Сила тертя прикладена у точці дотику -тіл, лежить у площині їх дотику і напрямлена проти швидкості руху тіла по опорі .При ковзанні тіла по опорі модуль сили тертя записують у вигляді формули Кулона-Алеонтона

, де N - реакція опори

- коефіцієнт тертя ковзання

Найважливішим у динаміці є три закони Ньютона .Вони пояснюють взаємозв'язок сил, характеристик тіл та їх руху .

І Закон . Якщо рівнодіюча всіх сил, прикладених до матеріальної точки, дорівнює нулю, то точка знаходиться у стані спокою або рівномірного і прямолінійного руху.

Отже, стан спокою і рівномірного прямолінійного руху з точки зору динаміки не відрізняються .

І І Закон Зміна імпульсу за інтервал часу дорівнює рівнодіючої сили і відбувається за напрямком її дії.

 ;  

Отже,

Отже, в інерційній системі відліку прискорення частинки пропорційне результу­ючій прикладних до неї сил і обернено пропорційне масі частинки. Якщо з бігом часу рівнодіюча не змінюється, тіло рухається рівноприскорено.

 

Якщо то і

ІІІ Закон  Сили, з якими два тіла діють одне на одне ,однакові за модулем, проти­лежні за напрямком , . Ці сили прикладені до різних тіл.

 

 

 

 

 

 

 

 

Алгоритм розв'язання задач

 

Необхідно  звернути увагу на вірне викори­стання ІІ закон Ньютона;

1. Спочатку треба зробити малюнок, на якому вказати систему відліку.
2. Вказати усі сили , які діють на тіло.
3. Вказати напрям швидкості і прискорення .
4. Записати II рівняння Ньютона у векторному виглядати
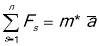
5. Векторне рівняння 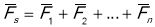спроеціровать на координатні вісі:

;             

де , 

6. Якщо рухається декілька тіл, які зв'язані між собою, то необхідно для кожного з них окремо виконати дії, що вказані у пунктах 1-5 і розв'язати сполучену систему рівнянь.
7. Якщо тіло рухається по колу, то проекція прискорення на вісь "у" це доцентрове прискорення .Тому по II закону Ньютона ми маємо :

або ,

де F- сума проекцій на вісь у сил, які діють на тіло.

 

Приклади розв'язання задач

 

Приклад 1.

Вагон масой 20 тн рухається рівносповільненно з прискоренням

0,3 м/с2 і початковою швидкістю 54 км/год. Знайти силу гальмування що діє на вагон, час гальмування і переміщення до зупинки.

Дано:   СІ

 

 

 

 

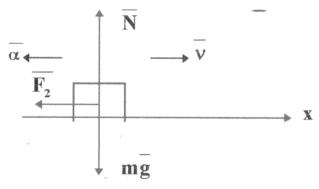
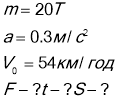
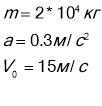
На тіло діють : сила тяжіння ; сила реакції опори і сила гальмування, - ;

Запишемо друге рівняння Ньютона у векторному вигляді

(1)

За додатковий напрям вісі х візьмемо напрям руху вагона. Так як рух рівносповільнений, вектор прискорення напрямлен у бік, протилежний напрямку руху. Спраекціруємо рівняння (1) на вісь х .

 

Час руху вагона до зупинки, і пройдений шлях знайдемо зрівнянь кінематики

т.я. то  

Відповідь: Сила гальмування 6кН, час гальмування 50с, шлях до зупинки 375м

 

Приклад 2.

Людина маса якої 70 кг. Піднімається у ліфті, який рухається в рівно-сповільнено у гору з прискоренням 1 м/с2. Визначити силу тиску людини на підлогу кабіни.

Дано:

 

 

 

 

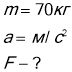
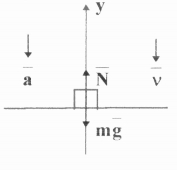На людину діє сила тяжіння і сила реакції підлоги кабіни. Прискорення напрямлено униз

Знайдемо проекцію цих векторів на вісь у.

За третім законом Ньютона сила тиску людини на пол кабіни по модулю дорівнює силі реакції пола кабіни. Отже , Р = N = 616 Н

Відповідь: Сила тиску людини на підлогу кабіни 616Н

 

Приклад 3.

Вантаж масою 45кг переміщається дією сили 294 Н ,яка напрямлена під кутом 30° до горизонту .Коефіцієнт тертя вантажу 0, площину 0,1. Визначити прискорення , з яким рухається вантаж .

Дано:

 

 

 

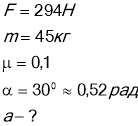
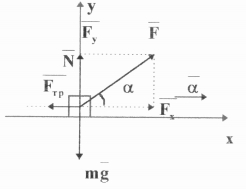
На вантаж діють сили: сила тяжіння - ;сила тертя - ; сила тяги - ; сила реакції опори - .

Запишемо третій закон Ньютона у векторному вигляді:

Вибираємо напрямки вісі х і у.

Знайдемо проекцію сил і прискорення на вісь х і у.

  

Зрівняння (3) знайдемо (4)

Ми знаємо, що . Отже, (5)

Підставимо рівняння (5) у рівняння (2)

Відповідь: Вантаж рухається з прискоренням 5,9м/с²

 

Приклад 4

Автомобіль масою 1 т піднімається у гору схил якої 30° під дією сили тяги 4кН . Знайти прискорення автомобіля, враховуючи, що сила опори не залежить від швидкості і складає 0,1 від сили нормальної реакції опори .

Дано:   СІ

 

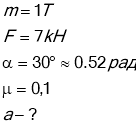
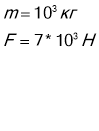
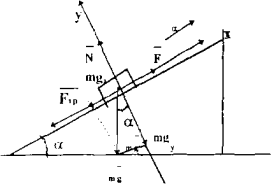На автомобіль діють сили:

- сила тяжіння - mg

- сила нормальної реакції - N

- сила тяги -

- сила тертя -

Вісь х напрямлено в бік рухe автомобіля . Запишемо II закон Ньютона у вектор­ному вигляді:

Знайдемо проекцію силі прискорення на вісь х і у .

  

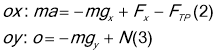
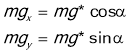
Ми знаємо, що . N знайдемо з рівняння (2)

. Тоді рівняння (1) можливо записати так :

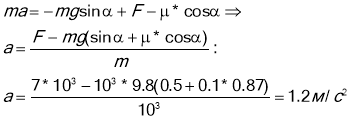
 Відповідь: прискорення автомобіля 1,2м/с²

 

 Приклад 5

 

Дано:   СІ

 

 

 

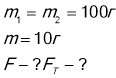
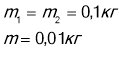
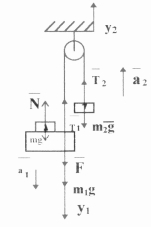Так як нить невагома і нерастяжима, сила натягу на всіх ділянках однакова і всі вантажи рухаються з однаковим прискоренням. Отже, Т₁=Т₂=Т; а₁=а₂=а.

Розглянемо сили, що діють на кожне з тіл. На перше тіло :

•       сила тяжіння -
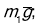
•       сила натягу -

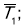
•       сила тиску - ;

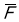На друге тіло :

- сила тяжіння - і сила натягу - Т₂

На перевантаж: сила тяжіння - сила реакції опори -

Запишемо ІІ рівняння Ньютона для кожного з тіл :

 (1)

  (2)

  (3)

Вісь у напрямлена в бік руху кожних з тіл . Тому у проекції на вісь у ми маємо :

  (4)  Треба врахувати, що F=N за ІІІ законом Ньютона

   (5)  Додамо всі рівняння :

   (6)

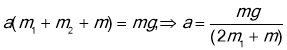; (7)

Суму F, з якої перевантаж діє на тіло , знайдемо з рівняння (6)

(8) Сила тиску на вісь

Силу натягу Т знайдемо з рівняння (5)

  (9)

Підставимо рівняння (7) у рівняння (8)

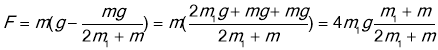
Щоб обчислити , підставимо рівняння (7) у рівняння (9)

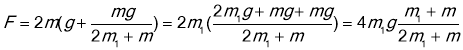
Відповідь:

 

Приклад 6.

Автомобіль масою 5т проїзжає по опуклому мосту зі швидкістю 21,6 км/год. З якою силою він натискає на середину моста, якщо його кривизна 50м.

Дано:   СІ

 

 

 

 

 

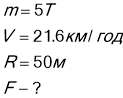
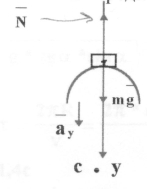
На автомобіль діють сили :

•       сила тяжіння -
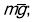
•       сила нормальної реакції моста -

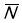
Вісь у напрямлено вздовж радіуса - R .

Рівняння Ньютона у векторному виді:

Проецирування рівняння на вісь у ми маємо ;

 де

За ІІІ законом Ньютона F=N=4.5*10⁴H

Відповідь: Автомобіль натискає на середину моста з силою 4,5*10⁴Н.

 

Приклад 7 .

Кулька масою 200 г. підв'язана до ниті і рухається у горизонтальній площині по колу з сталою швидкістю . Визначити швидкість кульки і період її обертання по колу якщо довжина ниті 1 м ,а кут з вертикаллю 30°.

 

Дано:   СІ

  

 

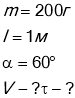
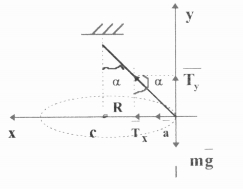
На кульку діють лише сила тяжіння mg і сила натягу нитки Т. Запишемо ІІ рівняння Ньютона .

Спроецієрумо рівняння на вісі х і у

 

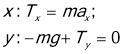
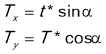
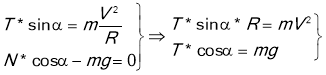Поділимо рівняння:

  

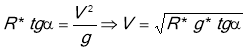
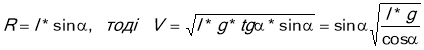
Відповідь: швидкість руху кульки 3,8 м/с, а період обертання 1,4с.

 

Приклад 8 .

Кулька закріплена на нитці довжиною 1 м і здійснює коливання у вертикальній площині .Знайти силу натягу нитки , коли вона утворює з вертикаллю кут 60°. Швидкість кулі у той час 1,5 м/с.

Дано:  СІ

   

 

 

 

На кульку діють сила тяжіння і сила натягу нитки

Вісь у напрямлено вздовж нитки

Знайдемо проекцію сил і прискорення на вісь у .

 

тоді   тому:

 

Відповідь: Сила натягу нитки 3,6Н.

 

Задачі

 

1.    Тіло масою т = 0.5кг рухається прямолінійно так, що залежність шляху S, що проходить тіло на протязі часу t, має вигляд: S = А–Вt+ Сt²–Dt³, де С = 5 м/с² , D = 1м/с³. Знайти силу F, що діє на тіло наприкінці першої секунди руху.
2.    Тіло масою 1.5кг рухається  прямолінійно так, що залежність шляху S, що проходить тіло на протязі часу t, має вигляд:   S=     =А sin t, де А = 5 см,  =  рад /с. Знайти силу F, що  діє  на тіло через t = 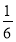с після початку руху.
3.    Вагон масою 20 т рухається рівносповільнено с прискоренням  0.3 м/с² та почаиковою швидкістю 54 км/год. Знайти силу, що діє на вагон, час руху вагона до зупинки та переміщення вагона.
4.    До нитки підвішений вантаж масою т = 1 кг. Знайти силу натягу нитки Т, якщо нитку з вантажем: а) піднімати с прискоренням а = = 5 м/с² . б) опускати з тим же прискоренням.
5.    Вантаж масою 50кг рівноприскорено піднімають заряд допомогою канату вертикально вгору на протязі двох секунд на висоту 10м. Визначити силу натягу канату.
6.    Людина масою 70кг піднімається в ліфті, що рухається рівносповільнено вертикально вгору с прискоренням 1 м/с². Визначити силу тиску людини на підлогу кабіни ліфту.
7.    Автомобіль масою 1 т піднімається поля шосе на схилі з кутом 30⁰ під дією сили 7кН. Знайти прискорення авьомобіля, якщо сила опору поверхні шосе не залежить від швидкості і складає 0.1 від сили нормальної реакції опори.
8.    Під час руху на автомобілі масою 1т діє сила тертя, k = 0.1. Знайти силу тяги мотору автомобіля, якщо він рухається з постійною швидкістю: а) вгору з схилом 1 м на кожні 25 м шляху. б) під гору з тим же схилом.
9.    Автомобіль з вантажем масою 5т рухається поля випуклому мосту  зі швидкістю 21.6 км/год. З якою силою він тисне на середину моста, якщо радіус кривизни моста 50 м?
10. Кулька масою 500г підвішена на нитці довжиною 1м. Вона здійснює коливальний рух в вертикальній площині. Знайти силу натягу нитки в ту мить, коли вона утворює з вертикаллю кут 60⁰. Швидкість кульки в цю мить 1.5 м/с.
11. Літак відривається від землі при v = 80 км/год. Яку силу тяги дає при цьому  двигун, якщо маса його 1026кг, довжина пробігу 150м, а коефіцієнт терть 0.02.  

 

Закони збереження

 

Основні поняття, закони і формули

 

Найбільш загальною векторною характеристикою поступального руху є імпульс тіла р. Це добуток маси тіла на його швидкість руху. ,

З 2 рівняння Ньютона вже відоме, що ; у скалярному вигляді ; де dP - зміна імпульсу тіла за інтервал часу  dt.

  - це імпульс сили.

Отже, імпульс сили дорівнює зміни імпульсу тіла. Для визначення імпульсу системи тіл або точок необхідно знайти векторну суму імпульсів окремих частин системи.

Якщо система замкнена (ізольована) і на неї не діють зовнішні сили (або вони весь час зрівноважені),то і зміна імпульсу відсутня: , а отже, імпульс системи лишається незмінним

Це твердження називають законом збереження імпульсу для замкненої системи тіл.

V_i- швидкості тіл у початковий, а - швидкості цих же тіл у будь-який іншій момент часу. Це універсальний закон , тобто виконується завжди. На відміну від буденного розуміння роботи як корисної діяльності людини у фізиці роботу А виконує сила , рухаючи довільне тіло на відстань уздовж лінії своєї дії

  

Якщо між векторами сили і напрямом переміщення кут ,то формула матиме вигляд Роботу змінної сили треба розраховувати по формулі 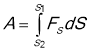. Сила перпендикулярна до переміщення , не виконує роботи і не змінює модуль швидкості тіла.

Потужність - це робота, яка виконується за одиницю часу.

 

Якщо вектори мають однаковий напрям потужність можна визначити:

Енергія Е - це скалярна фізична характеристика усіх форм руху матерії та варіантів її взаємодій.

Енергію механічного руху називають кінетичною Ек, а енергію механічної взаємодії - потенціальною Еп.

Зміна енергії тіла ( системи) Е дорівнює роботі А, яку виконала система, або яку виконали над нею .

  [E]-Дж

Повна механічна енергія, це сума кінетичної енергії і потенціальної

Е=Ек+Еп.

Виконану роботу можна обчислити за зміною його кінетичної енергії

А=Ек₂-Ек₁;  

або за зміною його потенціальної енергії

Якщо на тіло діє сила тяжіння, то вона виконує роботу

отже

Кінетична енергія завжди позитивна, а потенціальна може мати і від'ємне значення. Ще одним видом механічної потенціальної енергії є енергія деформації. Стиснена на відстань Х пружина з жорсткістю К має потенціальну енергію.

Тоді

так як при розпрямленні її на відстань х середня сила дорівнює половині максимальній.

Надзвичайно важливе теоретичне та практичне значення має за­кон збереження енергії. Енергія має безліч форм : механічну, теплову енергію молекулярного руху, електричну енергію систем зарядів. Одна форма може переходити в іншу.

Якщо сил тертя немає і тепло не утворюється, то механічна енергія Е=Ек+Еп залишається сталою у процесі руху або взаємодії тіл. Це твердження відоме як закон збереження механічної енергії. Наприклад, під час вільного падіння без опору повітря виконується співвідношення; .

Прикладом застосування законів збереження імпульсу і енергії є удар. Удар - це дуже короткочасна взаємодія двох тіл та більше. Абсолютно пружній удар-тіла не деформіруються під час взаємодії і їх кінетична енергія після удару перетворюється у кінетичну. Для такого удару виконується і закон збереження імпульсу і закон збереження енергії.

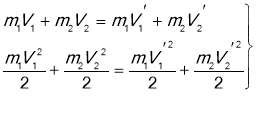
Після перетворення рівняння (1)і(2) можно сполучити що

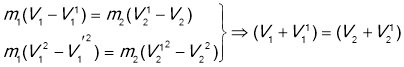
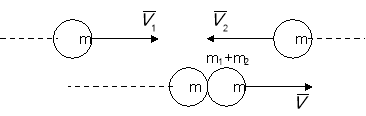абсолютно не пружній удар - після співудару тіла рухаються як одне тіло.

 

 

 

 

 

Швидкість їх руху можна знайти з закону збереження імпульсу:

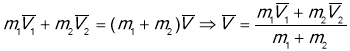
Якщо тіла рухаються назустріч ,то вони будуть рухатись в той бік .в який рухається тіло з більшим імпульсом. Якщо то

Закон збереження механічної енергії не виконується, т. як частина кінетичної енергії перетворюється у теплову енергію. Цю "втрату" енергії можна визначити :

Коли на тіло діють зовнішні сили , повна механічна енергія системи змінюється. При цьому виконується співвідношення   , де А-робота зовнішніх сил. Це співвідношення можна використовувати і коли діють неконсервативні сили ( сила тертя, опору). Тоді А - це робота цих сил.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Алгоритм розв'язання задач з теми

 

1.     Правила розв'язання задач о роботі сталої сили зводяться до наступного:

а) встановити, роботу якої сили треба визначити і записати формулу: , де F - може бути окремою силою і рівнодією

б) зробити малюнок і на ньому вказати всі діючи сили

в) визначити кут між напрямками сили, роботу якої треба визначити, і напрямком переміщення

г) якщо сила в умові задачі не задано, її знайти з ІІ закону динаміки

д) знайти модуль переміщення (якщо воно невідомо) по рівнянням кінематики

е) підставити всі знайдені величини у формулу роботи і виконати розрахунки

2.     Для визначення роботи змінної сили необхідно:

а) зробити малюнок і вказати всі сили

б) під час запису рівняння для визначення сили пам'ятайте, що

де  - значення сили тока на початку переміщення

- значення сили на кінці переміщення.

 Якщо, а то або  де К- коефіцієнт пружності.

г) у загальному вигляді робота, як скалярна величина, визначається 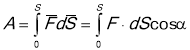, де - переміщення, на якому F стала величина.

3.     Закон збереження енергії - один з основних законів. Цей закон зв'язує початковий і кінцевий стан системи і полегшує розв'язання задач з динаміки, тому що можна не розглядати сили, які діють між тілами.

а) зробити малюнок і записати формулу закона збереження енергії

б) встановити перший і другий стани системи

в) вибрати нульовий рівень відліку потенціальної енергії

Зручніше вибирати  або по найнижчому положенню, яке займає тіло під час свого руху, або від рівня, на яке описукається тіло, коли переходить з першого положення у друге.

г) вказати всі зовнішні сили, що діють на тіло в довільній точці і відмітити кінематичні характеристики механічного стану системи

д) скласти рівняння для роботи зовнішніх сил і повної механічної енергії тіла (системи) в положеннях І і ІІ і підставити їх у закон збереження енергії для визначення невідомої величини. Якщо невідомих більше одного, то закон збереження енергії доповнити основним рівнянням динаміки матеріальної точки. Розв'язуючи систему рівнянь можна визначити невідому величину.

 

 

 

 

Приклади розв'язання задач

 

Приклад 1:

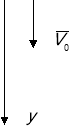
Тіло маса якого 0,2 кг падає з висоти 1м з прискоренням 8м-с. Знайти зміну імпульса тіла.

Дано:

  

 

Імпульс змінюється тому ,що тіло рухається з приско­ренням і його швидкість збільшується

 (1)

Напрям  вісі У униз. Спроеціруємо рівняння (1) на вісь У

Тіло почало рух із стану спокою. Отже для знаходження швидкості

V використаємо рівняння:

Отже

Відповідь: імпульс тіла 0,8 кг*м/с

 

Приклад 2

Молекула маса якої 5 *10^-26 кг. Рухається  зі швидкістю 500 м/с під кутом 30° до перпендикуляру зі стінкою. Знайти імпульс сили, що сполучила стінка під час удару.

Дано:

 

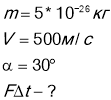
Вісь У розташована вертикально а вісь Х перпендикулярно до неї. З ІІІ закону Ньютона випливає, що імпульс сили що діє на стінку чисельно дорівнює імпульсу сили, що діє на молекулу. З ІІ закону Ньютона ми знаємо що

Запишемо це рівняння у проекціях на вісі Х та У

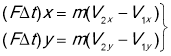 Цей удар пружній тому а .

Тоді маємо:

  

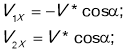
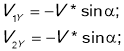
отже:   

По визначенню, імпульс сили

Отже,

Відповідь: стінка сполучила імпульси сили 4,35*10^-23Нс

 

Приклад 3

Снаряд масою 100кг рухається горизонтально уздовж залізничної дорозі зі швидкістю 500м/с.Він попадає у вагон з піском, маса якого 10т, і залишається там .Знайти швидкість вагона , якщо він рухався зі швидкістю 36 км/год назустріч снаряду.

Дано:   СІ

 

 

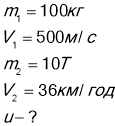
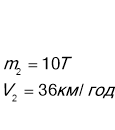
Запишемо рівняння для напруженого співудару:

Вісь Х співпадає з напрямком руху снаряда

Спроєціруємо рівняння на вісь Х:

  

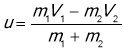
Відповідь: напрям руху вагона не змінився, а його швидкість руху стала 5м/с.

 

Приклад 4

Граната, що рухалася зі швидкістю 15 м/с розірвалася на два уланка маса яких 6 і 14 кг. Швидкість більшого уланка збільшилася до 24 м/с по напрямку руху. Знайти швидкість і напрям руху меншого уланку.

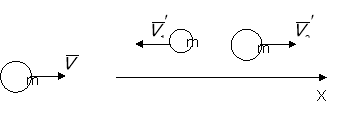Дано:

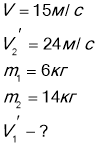
Вісь х напрямлена вздовж руху гранати. Запишемо рівняння у векторному вигляді, а потім спроєцируємо на вісь Х  , де

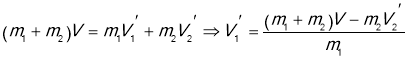
Відповідь: Знак (-) означає ,що менший уланок почне рухатися у бік протилежний руху більшого уланка, зі швидкістю 6м/с

 

Приклад 5

Куля, що рухається зі швидкістю 400 м/с попадає у вал і проходить до зупинки 0,5м. Визначити силу опору вала кулі ,якщо її маса 24г.

Дано:  СІ

  

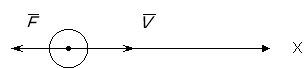
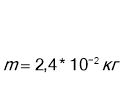
Вісь Х напрямлена вздовж руху кулі. Отже , а , тому , інакше:

По умові Е=0 , т.я. куля зупиняється, отже (2)

З рівнянь (1) і (2) випливає, що

Відповідь:

 

Приклад 6

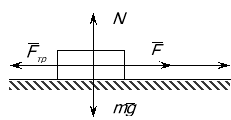
Потяг масою 600т набув швидкість 60 км/год, коли пройшов 2,5км. Яку середню потужність він розвив, якщо коефіцієнт тертя 0,005?

Дано:   СІ

 

Вісь х напрямлена вздовж руху потяга. На потяг діють сили: - сила тяжіння, N- сила нормальної реакції; F- сила тяги ; F_тр- сила тертя.Зміна кінетичної енергії дорівнює роботі зовнішніх сил т. як

, де А₁-робота сили тяги; а Тому: Е=А₁+А₂ (1), А₂- робота сили тертя;

Робота сили тяжіння і сили N=0 , т.к. =90°. Для горизонтальної площини  (5)

Отже маємо, якщо підставимо (2)-(5) у рівняння (1)

 Т. як треба визначити середню потужність <N>, то треба взяти і середню швидкість <\/>, а для рівноприскореного руху вона визначається так :

Для потужності маємо:

Відповідь: Потяг розвив середню потужність 0,52МВт

 

Приклад 7

Вантаж масою 2 кг падає з висоти 5 м у м'який ґрунт на глибину 5 см. Визначити середню силу опору ґрунту

Дано:  СІ

 

 

 

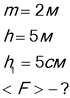
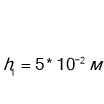
Вісь У напрямлена вертикально вгору. Початок вісі візьмемо на глибіні h₁ від поверхні землі на ділянці СО діє зовнішня сила, тому

Е₀ - це механічна енергія вантажа у точці В

Е - механічна енергія на глибині. Т. як У=0; V=0, то і Е=0

А=-Е₀ (1)

З другого бoку робота зовнішніх сил на ділянці СО дорівнює

Порівнявши рівняння (1)і (2) маємо:

Відповідь:

 

Приклад 8

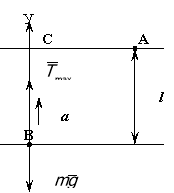
Куля масою т підвішена на нитці довжиною l . Її відхилили на кут 90°від вертикалі і відпустили. Визначити максимальну силу натягу.

Дано:

 

 

 

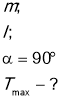
Сила натягу мах , коли тіло проходить положення рівноваги, тобто знаходиться у точці В На тіло діють дві сили : mg - сила тяжіння і Т - сила натягу

ІІ рівняння Ньютона має вигляд:

Вісь У напрямлена як і вектор а, спроєцируємо рівняння на вісь У і маємо (1) ; а - доцентрове, прискорення тому:

Але l =R, тому ; З рівняння (1) випливає, що

Для визначення енергії   Отже   

Відповідь: максимальна сила потягу 3mg.

 

Приклад 9

Знайти роботу ,яку треба виконати щоб стиснути пружину жорсткістю 29,4Н/см на 20 см Деформація пружини.

Дано:  СІ

  

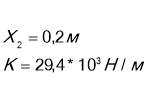
Робота по стисненню пружини дорівнює зміні її потенціальної енергії

 Отже

Відповідь: по стисненню пружини була виконана робота 58,8 Дж

 

Приклад 10

Кулька рухається горизонтально і попадає у шар, який закріплен на стержні. Маса Кульки у 1000 разів менша за масу кулі. Відстань від точки закріплення до центра кулі 1м. Знайти швидкість кульки якщо видано, що під час удара стержень відхилився на кут 10°

Дано:

 

 

 

 

 

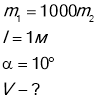
Вісь Х напрямлена вздовж руху кульки. Для визначення швидкості кулі залишимо закон збереження імпульсу і с проецируємо рівняння на вісь Х.

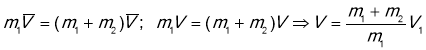(1)

де V - швидкість кулі до співудару кулі; - швидкість кульки і шару після співудару .Щоб знайти що швидкість застосуємо закон збереження енергії. Кінетична енергія кульки й кулі перетворилася в потенціальну енергію

(2)

Висота h невідома і її знайдемо з малюнку

Але ми знаємо ,що , тому . Підставляємо це визначення h у рівняння (2)

(3).

А зараз рівняння (3) підставляємо у рівняння (1) і знайдемо швидкість кульки:

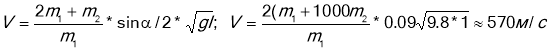
Відповідь: швидкість кульки 570 м/с.

 

Приклад 11

Дві пружини однакової довжини які мають жорсткість К₁=9,8Н/см К₂=19,6Н/см, з'єднанні між собою кінцями(паралельно). Яку роботу треба виконати ,щоб розтягнути пружини на S₀=1см? Чому буде дорівнювати робота ,якщо пружини будуть з'єднані одним кінцем між собою (послідовне).

Дано:   СІ

 

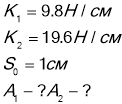
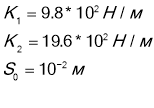
Щоб розтягнути, або стиснути пружину ,треба прикласти силу, модуль якої залежить від пружних властивостей пружини (закон Гука)

 

Робота такої сили може бути визначена за рівнянням:

 

Знайдемо жорсткість при різних формах стискання пружини .

 

 

 

 

 

 

Паралельне з'єднання                 Загальне розтягнення однакове модуль сили, що деформує пружини, дорівнює сумі модулів сил отже, ; ; Знаходимо що, Тому

Послідовне з'єднання                 При послідовному з'єднанні натяг кожної пружини дорівнює зовнішньої сили . Загальне видовження дорівнює сумі видовженню кожної пружиною . З закону Гука отже,

Відповідь: щоб розтягнути пружини при паралельному з'єднанні треба виконати роботу А₁=0,147Дж, а при послідовному з'єднанні пружин роботу треба виконати меншу: А₂=0,037Дж

 

Задачі

 

1. Відзначити роботу, яку треба виконати, щоб стиснути пружи­ну на Х=10см, якщо для її стискання на 1см необхідна сила 100 Н.

( А=50Дж)

 

2. Вагон масою М =2*10⁴ кг рухаючись зі швидкістю V₀=0/5 м/с, ударяються в два нерухомі пружинні буфера. Знайти найбільше стиснення буферів X, якщо буфер стискається на один см при дії сили 5*10⁴ Н.

(Х=0,22м.)

 

3. Діючи постійною силою F= 200Н, підіймають вантаж М=10кг на висоту Н=10м. Яка при цьому здійснюється робота ? Яку потенційну енергію буде мати при цьому підіймаємий вантаж ?

(А =2*10³ Дж, П=10³ Дж.)

 

4. Літак для зльоту повинен мати швидкість Уо==25 м/с. Довжина пробігу до зльоту S=100м. Яка потужність моторів літака при зльоті, якщо маса літака М=1000кг та коефіцієнт опору k=0.02?

(М=83100Вт).

 

5. Тіло кинуте вертикально угору зі швидкістю Vо == 16м/с. На якій висоті h=? кінетична енергія тіла буде дорівнювати потенційній енергії ?

(h=б.5м)

 

6. З якою початковою швидкістю треба кинути м'яч з висоти h, щоб він підстрибнув на висоту 2h? Удар пружний.

 

7. Падаючим з висоти h =1,2 м вантажем забивають полю, яка від удару заходе в землю S=2см. Визначити середню силу удару та його тривалість, якщо маса вантажу М=500кг, а маса полі значно менша за масу вантажу.

(F=3*10⁵ Н; t ==8*10^-3 с.)

 

8. Ковзаняр масою М=70 кг, стоячи на ковзанах на льоду, кидає у горизонтальному напрямі камінь масою М=3кг зі швидкістю V₁=8м/с. Знайти на яку відстань відкотиться при цьому ковзаняр, якщо відомо, що коефіцієнт тертя об лід k=0,02.

(S=0,29м)

 

9. Людина стоїть на нерушимій теліжці і кидає горизонтально камінь вагою М₁=8кг зі швидкістю V₁=5м/с. Визначити яку при цьому людина виконує роботу, якщо вага теліжки разом з люди­ною М₂=160кг. (А=105 Дж)

 

10. Куля яка летить горизонтально зі швидкістю V₁=-400м/с, попадає у брусок, підвішений на ниті довжиною l=4 м, і застряє у ньому. Визначити кута ,на який відклониться брусок, якщо вага кулі М₁=0,02, а бруска М₂=5кг. (α=15 °, tgα=105 Дж.)

 

11. Молот вагою М₁=5т ударяє по розколеній болванці. Вага болванці, яка лежить на ковадло, і деформує болванку. Вага ковадла разом з болванкою М2=20т. Визначити коефіцієнт корисної дії при ударі молот рахуючи удар напругим. (η=93%)

 

12. Яку роботу треба зробити щоб заставити тіло яке рухається вагою М=2кг : 1)Підвищити свою швидкість V₁ =2 м/с до V₂=5м/с. 2) Зупинитись при початковій швидкості V₂=8м/с. (А₁=21Дж; А₂=64 Дж)

 

 

13. Молекула масою М=4,65*10^-26 кг, що летить по нормам до стінки по­судини зі швидкістю М=600м/с, вдаряються о стінку та пружно відскакує від неї без витрати швидкості. Отриманий за час удару зі стінкою.

 

14. Молекула масою М=4,65*10^-26 кг, що летить зі швидкістю V=600м/с, вдаряються об стінку посудини під кутом α=60 ° за нормами та пружно відскакує од неї, без втрати швидкості. Знайти імпульс отриманий стінкою під час удару.

 

15. Людина масою М₁=60кг, біжуча зі швидкістю V₁==8км/ч доганяє  возик масою М₂=80кг рухаючись зі швидкістю V₂=2,9км/ч, та застрибує на неї. З якою швидкістю буде рухатися возик ? З якою швидкістю буде рухатися возик, якщо людина бігла на зуст­річ ?

 

16. Снаряд масою М=100кг, що летить уздовж залізничного шляху зі швидкістю V₁=500 м/с, попадає у вагон з піском маса котрого М₂=10т, та застряє в ньому. Яку швидкість отримає вагон якщо: а)Вагон стоїть нерухомо; б)Вагон рухався зі швидкістю V₂=36 км/год тому ж напрямку що і снаряд; в)Вагон рухався зі швидкістю V₂=36км/год напрямку протилежному руху снаряда.

 

17. Граната що летить зі швидкістю V=10 м/с розірвалась на два оскол­ки. Більший осколок маса котрого відповідно дорівнює 0,6 маси від усієї гранати продовжував рухатися у попередньому напрямі, але при збільшений швидкості И₁=25м/с. Знайти швидкість И₂=? меншого осколка.

 

18. Яку роботу А треба виконати, щоб примусити рухаючись тіло М=2 кг: а)3більшити швидкість від V₁=2м/с до V₂=5м/с. б)3упинитись при початковій швидкості Vо=8м/с ?

 

19. Камінь кинутий по поверхні льоду зі швидкістю V=3м/с, пройшов до зупинки S=20,4м. Знайти коефіцієнт тертя k об лід.

 

20. Вагон масою М=20т рухаючись рівносповільнено з початковою швидкістю Vо=54км/ч, під дією сили тертя Тмр=6кН через деякий час зупиняється. Знайти роботу А, і відстань S ,яку вагон пройде до зупинки.

 

21. Тіло масою М₁=2кг рухається назустріч другому тілу масою М₁=1,5кг та абсолютно не пружно співударяється з ним. Швид­кості тіл безпосередньо перед ударом були V₁=1м/с та V₂=2м/с. Який час t будуть рухатися ці тіла після удару, якщо коефіцієнт тертя k=0,05?

 

22. Зі знаряддя вагою 5т вилетів снаряд вагою М=100кг кінетична енергія снаряда при вилиті Е_КГ=7,5МДж. Яку кінетичну енергію Е_КІ одержить знаряддя внаслідок віддачі?

 

23. Куля яка летить горизонтально попадає у кулю підвішену невисовому жорсткому стержні, і застряє у ньому. Вага пулі М₁ =5гр, а вага кулі М₂=0,5кг. Швидкість пулі V₁=500м/с при якій крайній відстані І від центру кулі до точки подвіса стержня, куля від удару пулі підіймається до верхньої точки кола.

 

24. Куля вагою М₁=3кг рухається зі швидкістю V=4м/с і б'ється о нерушиму кулю такої ж ваги. Рахуючи удар центральний та абсолютно попружний, знайти кількість тепла Q яка віддалась при ударі.

 

25. Стальна кулька падаючи з висоти h=1.5м на стальну плиту, відскакуєвід неї зі швидкістю V₂=0.75*V₁, где V₁- швидкість з якою він підлетить до плити . На яку висоту пі підлетить кулька ? Скіль­ки часу пройде до другого удару об плиту?

 

26. Камінь прив'язаний до мотузки довжиною Ь=50см, рівномірно обертається у вертикальній площині. При якій частоті обертання n мотузка розірветься, якщо вказано, що вона рветься при силі на-тяжіння, рівного десятикратній силі притягання, що діє на камінь.

 

27. Камінь масою М=0,5кг прив'язаний до мотузки довжиною L=50см рівномірно обертається в вертикальній площині. Сила натягу мотузки у нижній точці кола Т=44Н, на яку висоту h підніметься камінь, якщо мотузка обірветься тоді коли швидкість буде спрямована вертикально догори?

 

28. Знайти роботу А, яку треба зробити, для того щоб стиснути пружину на  L=20см, якщо сказано, що сила F пропорційна стисканню L і жорсткість пружини k=2,94 Н/м.

 

29. З якою швидкістю V рухається вагон вагою М=20т, якщо при ударі о стіну кожний буфер стиснувся на L=10 см. Жорсткість пружини кожного буфера k=1МН/м

 

30. До нижнього кінця пружини, підвішений вертикально, приєднана інша пружина, до кінця якої прикріплено гру з. Жорсткість пружин k₁=k₂, зневажаючи вагою пружин по зрівнянню з вагою вантажу, знайти відношення Ері/Ері потенціальна енергія цих пружин.

 

31. На двох паралельних пружинах однакової довжини висять на невисомому стержні довжиною L=10см. Жорсткість пружини k₁=2Н/м і k₂=3Н/м. У якому місці стержня треба повісити вантаж так, щоб стержень залишився горизонтальним?

14. Яка відбувається робота при перенесенні крапкового заряду 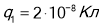з нескінченності в крапку, що знаходиться на відстані 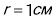від поверхні кулі радіусом 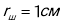з поверхневою щільністю заряду ?

( )

 

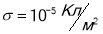15. Кулька масою і зарядом переміщається з крапки А, потенціал якого в крапку В, потенціал якої . Чому була дорівнює його швидкість у крапці А, якщо в крапці У вона стала ?

( )

 

16. Знайти швидкість електрона ( ; ), що пройшов різницю потенціалів ; ; .

( ; ; )

 

17. Електричне поле утворено позитивно зарядженої нескінченно довжиною ниткою. Рухаючи під дією цього полючи від крапки, що знаходиться на відстані від нитки, до крапки ,  - частка змінила свою швидкість від до . Знайти лінійну щільність заряду на нитці. ( ; )

( )

 

18. Електричне поле утворено позитивно зарядженої нескінченно довжиною ниткою з лінійною щільністю заряду . Яку швидкість одержить електрон під дією полючи, наблизивши до нитки з відстані до відстані від нитки?

( )

 

19. Біля зарядженої нескінченно протяжної площини знаходиться крапковий заряд під дією полючи заряд переміщається по силовій лінії на відстань , при цьому відбувається робота . Знайти поверхневу щільність заряду на площині.

( )

 

20. Різниця потенціалів між пластинами плоского конденсатора дорівнює . Площа кожної пластини заряд . На якій відстані друг від друга знаходяться пластини?

( )

 

21. Між двома вертикальними пластинами, що знаходяться на відстані друг від друга, на нитці висить заряджена кулька, маса якого . Після того, як на пластини була подана різниця потенціалів , нитка з кулькою відхилилася на кут . Знайти заряд кульки.

( )

 

22. Електрон з початковою швидкістю влітає в плоский конденсатор паралельно пластинам на рівній відстані від них. До пластин конденсатора прикладена різниця потенціалів . Відстань між пластинами , довжина конденсатора . Яка була початкова швидкість електрона, якщо електрон не вилітає з конденсатора? Маса електрона , заряд електрона .

( )

 

23. Електрон ( ; ) рухається в плоскому горизонтальному конденсаторі паралельно його пластинам зі швидкістю . Напруженість полючи усередині конденсатора . Довжина пластин конденсатора . На скількох зміститься електрон у вертикальному напрямку при вильоті з конденсатора?

( )

 

24. Електрон ( ; ) улітає зі швидкістю в плоский горизонтальний конденсаторі паралельно його пластинам на рівній відстані від них. Відстань між пластинами , напруженість електронів у конденсаторі . Через скількох часів після того, як електрон влетів у конденсатор, він потрапив на одну з пластин?

( )

 

25. Вісім заряджених водяників крапля радіусом і зарядом кожна зливаються в одну загальну водяну краплю. Знайти потенціал великої краплі.

( )

 

26. Кулька, заряджена до потенціалу , має поверхневу щільність заряду рівну . Чому дорівнює радіус кульки?

( )

 

27. Площа кожної пластини плоского повітряного конденсатора , відстань між пластинами . Знайти ємність цього конденсатора.

( )

 

28. Потрібно виготовити конденсатор ємністю в. Для цього на парафінований папір товщиною наклеюють по обидва боки кухля станіолі. Який повинний бути діаметр цих кружків, якщо

( )

 

29. Радіус центральної жили коаксіального кабелю , радіус оболонки . Між центральною жилою й оболонкою прикладена різниця потенціалів . Обчислити напруженість електричного полючи на відстані від осі кабелю.

( )

 

30. Знайти ємність сферичного конденсатора, що складає з двох концентричних сфер радіусами і . Простір між сферами заповнено олією. ( ). Який радіус повинний мати кулю, поміщена в олію, щоб мати таку ємність?

( ; )

 

 

 

 

РОЗДІЛ ІІ МОЛЕКУЛЯРНА ФІЗИКА. ТЕРМОДІНАМІКА

 

Основні закони і поняття, формули

 

1.    Атомом називають найменшу частинку певного хімічного елемента. Яка зберігає хімічні властивості цього елемента. Молекула – найменша стійка частинка певної речовини, яка має її основні хімічні властивості.

Маси атомів і молекул дуже малі, тому в розрахунках використовують не абсолютні значення мас, а відносні.

Відносною малярною (абсолютною) масою речовини - називають відношення маси молекул до маси атома вуглецю .

.

В термодинаміці і в молекулярній фізиці замість маси користуються кількістю речовини, яка виражена в молях.

Моль – це кількість речовини, яка містить стільки молекул (атомів), скільки міститься атомів у вуглецю.

Число атомів або молекул, які містяться в одному молі речовини, називають сталою Авогадро.

N_A=6,0210²³моль^-1

Кількість речовини – це відношення числа молекул (атомів) у певному макроскопіч­ному тілі до числа Авогадро: .

Масу речовини, взятої в кількості 1моль називають малярною масою . Вона дорівнює добутку маси молекули на сталу Авогадро.

Кількість речовини зараз можна визначити інакше:

.

З закону Авогадро видимо, що моль газу за нормальних умов має об’єм

Тоді для газів кількість речовини можна визначити так: .

Нормальні умови: ;

.

2.    Основне рівняння молекулярно-кінетичної теорії визначає макроскопічну величину – тиск через концентрацію молекул -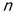, масу молекули і середню квадратичну швидкість їх руху:

   

Якщо згадати, що - середня кінетична енергія поступального руху молекули, то:

  

Але — це середня кінетична енергія поступального руху всіх молекул.

Термодинамічна температура – міра середній кінетичній енергії хаотичного руху молекул газа.

, де - це стала Бальцмана.

Тоді основне рівняння М.К.Т. має вигляд:

Середню швидкість поступального руху молекул можна визначити так:

;  

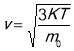Вивчення термодинамічних властивостей пари займає важливе місце. Це зумовлено тим, що процеси пароутворення і конденсації лежать в основі багатьох сучасних промислових і сільськогосподарських технологій.

3.    Стан тіл характеризують сукупністю декількох фізичних величин, які називають параметрами стану. Важливими параметрами для стану газу являються його об’єм 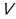, тиск - 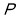і температура .

Стан газу, при якому всі його параметри не змінюються, якщо не змінюються зовнішні умови, називають рівноважним. Зміна стану газу називається термодинамічним процесом. Якщо під час зміни стану газу одним з параметрів не змінюється, процес називається ізопроцесом.

Рівняння для ідеального газу саме прості. Вони всі одержані експериментально.

Ідеальним називають газ, в якому можна знехтувати розмірами молекул та їх взаємодією. Співудари між молекулами відбуваються за законами абсолютно пружного удару.

4.    Ізотермічний процес – це процес зміни стану газу при незмінній температурі і маси газу.

 T=const

Бойль і Маріотт встановили, що для двох станів газу

5.    Ізобаричний процес – це процес відбувається при сталому тиску

 P=const

Залежність між об’ємом і температурою встановив Гей Люсак:

Дане двох станів газу відношення об’ємів прямо пропорційно відношенню термодинамічних температур:

;  , де - коефіцієнт об’ємного розширення

6.    Ізохоричний процес – це процес зміни стану газу при постійному об’єму

 V=const

Залежність між тиском і температурою встановив Шарль

; - температурний коефіцієнт тиску.

 

7.    З дослідів фактів для ідеальних газів випливає, що об’єднаний газовий закон:

- цей вираз називають рівнянням Клапейрона.

Його можна застосовувати для сталої маси газу .

Під час переходу газу з одного стану в другий змінюються всі три параметри:

8.    Для будь-якої маси газу, треба застосувати рівняння Менделєєва-Клапейрона:

, де М – малярна маса

R- малярна універсальна газова стала

 

Це рівняння можна записати інакше, якщо згадати, що густина

 

9.    Термодинамічна стала як сукупність множини атомів і молекул має внутрішню енергію . Внутрішня енергія – це сума енергій молекулярних взаємодій і енергія теплового руху молекул. Внутрішня енергія залежить від стану системи. Змінити внутрішню енергію можна або механічним способом, або теплообміном.

- І начало термодинаміки.

- зміна внутрішньої енергії газу;

Q – кількість теплоти, що надана тілу;

- робота, що виконана газом під час розширення.

;   

Для ізохорного процесу (V=const),

;  

Для ізобарного:   

Внутрішня енергія ідеального газу можна визначити:

, де - ступінь свободи.

- одноатомний газ

- двоатомний газ.

Для ізотермічного процесу: і

Для ізобаричного: .

Для адіабатного: ; 

10. Коефіцієнт корисної дії парової машини, що працює по циклу Карно дорівнює:

, де

Т₁ – температура нагрівника, а

Т₂ - температура холодильника

Q₁ – кількість теплоти, що отримана від нагрівника

Q₂ – кількість теплоти, що забрав холодильник.

- це робота, яку здійснює робоче тіло.

Тоді:

11. Закон збереження енергії у теплових процесах виражає рівняння теплового балансу:

 

, якщо тіло одержує тепло

, якщо тіло віддає тепло.

Тіла можуть знаходитися в одному з трьох станів: твердому, рідкому, газоподібному. При певних умовах вони можуть переходити з одного стану в інший.

а) Під час плавлення кристалічних тіл потенціальна енергія молекул або атомів збільшується на величину: , де - питома теплота плавлення.

б) під час пароутворення потенціальна енергія молекул пара збільшується, а кінетична енергія рідини зменшується на величину:

, де - питома теплота пароутворення.

в) При повному згорянні палива масою внутрішня енергія теплового руху молекул збільшується на величину:

, де - питома теплота згоряння палива.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Алгоритм розв’язання задач.

 

1. Якщо під час взаємодії тіл змінюється лише внутрішня енергія тіл без виконання роботи, то користуємося рівнянням теплового балансу.

Порядок розв’язання таких задач:

а) Прочитати умову задачі і встановити, у яких тіл внутрішня енергія зменшується, а у яких – збільшується. Звернути увагу, чи відбуваються у цих процесах агрегатні перетворення і які.

б) Скласти рівняння для тих, внутрішня енергія яких зменшується:

в) Скласти рівняння для тіл, внутрішня енергія яких збільшується

г) Прирівняти одержані суми

Під час такого запису рівняння треба від більшої температури віднімати меншу. Температура теплової рівноваги позначається буквою .

д) Якщо у задачі задається К.К.Д., то він являється співмножителем до .

Отже,

2. Під час взаємодії тіл відбувається перетворення однієї енергії в друг. Внутрішня енергія змінюється за рахунок виконання роботи тілом, або над тілом. Теплообмін не враховується.

а) Читая умову задачі встановити, у якого тіла змінюється внутрішня енергія і за яких умов.

Перевірити, що тепло не підходить і

 (1)

б) Якщо задається К.К.Д., то треба ще раз уважно прочитати умову задачі. Якщо робота виконується за рахунок зменшення внутрішньої енергії одного з тіл, то .

Якщо внутрішня енергія тіла збільшується за рахунок роботи, що виконана над тілом, то

в) Що записати рівняння (1), треба для і записати одне з рівнянь

 

Для

Для

3. Якщо взаємодіють багато тіл і при цьому підводиться тепло, змінюється внутрішня енергія і виконується робота, то треба використовувати І начало термодинаміки.
4. Якщо по умові задачі задані 2 стани газу, а маса під час переходу з одного стану в другий не змінюється, то:

а) прочитати умову задачі і зробити схематичний малюнок, на якому вказати всі параметри стану газу. Визначити, змінюються всі параметри, або один залишається незмінним.

б) Записати об’єднаний газовий закон для двох станів. Якщо газ знаходиться у циліндрі і його тиск змінюється за рахунок переміщення поршня, то рівняння Клапейрона можна записати так:

в) записати всі допоміжні умови, що вказані в умові задачі і розв’язати сполучену систему рівнянь.

5. Якщо задан один стан газу, або два стани, але з різною масою, то:

а) треба скласти рівняння Менделєєва-Клапейрона для усіх станів газу;

б) якщо дана суміш газів, то треба записати рівняння для кожного компонента;

в) зв’язок між тисками суміші встановити за законом Дальвитона:

г) записати математично додаткові умови задачі і розв’язати сполучену систему рівнянь.

6. Під час розв’язання задач на вологість треба користуватися таблицями пружності і густини насичених парів і застосувати формули відносної вологості:

;  

При однаковій температурі

а) Прочитати умову задачі і встановити чи є сухе повітря у парі рідини. Тоді ,

де - атмосферний тиск;

- тиск сухого повітря;

- тиск пари.

б) Для кожного стану записати рівняння Менделєєва-Клапейрона і формулу відносної вологості

Варто пам’ятати:

1.                що якщо задана температура насиченого пара, то його тиск і густину знаходимо по таблиці;
2.                якщо задана температура і тиск ненасиченого пара, то його густина і тиск визначаються з рівняння Менделєєва-Клапейрона;
3.                тиск насиченої пари при температурі кипіння дорівнює атмосферному тиску.

Отже:

1. Якщо термодинамічний процес протікає повільно (початковий і кінцевий стани рівноважні), то:

  

а) - коли немає пароутворення і конденсації

б) - коли переважає пароутворення або кипіння

і - це кількість речовини і маса рідини, що перетворилися на пару.

в) - переважання конденсації

і - це кількість і маса новоутвореної рідини.

2. Коли задачі пов’язані з вологістю, то термодинамічний процес можна схематично зобразити так:

  

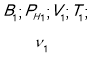
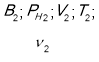
або

  

 

Приклади розв'язання задач.

 

Задача №1.

Скільки молів і молекул водню міститься в балоні об'ємом 50 м³ під тиском 767 мм рт.ст. при температурі 18°С? Яка густина газу?

Дано:    СІ

 

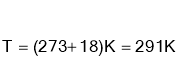
V, N. р?

 

Розв'язування. З рівняння Клапейрона-Менделєєва

  (1)

Число молів в об'ємі V визначають за формулою

  (2)

За відомими р, V, R і Т:

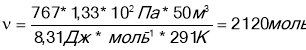
Число молекул n, які містяться в певному об'ємі, знаходимо, використавши сталу Авогадро N_A:

Густину газу ρ=m/V визначаємо з рівняння (1)

.

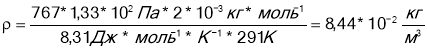
Відповідь: Густина газу дорівнює 8.44*10^-2 кг/м³ . В балоні об'ємом 50 м³ міститься 2120 молів і 12,76*10²⁶ молекул водню

 

Задача №2.

Який має бути найбільший об'єм балона, щоб він вміщав m=6.4 кг кисню при t=20°С, якщо його стінки витримують тиск р=16МПа?

 

 

 

 

Дано:    СІ

 

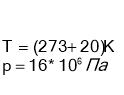
Розв'язування. З умови задачі випливає, що коли в балон помістити 6.4кг кисню, то тиск не повинен перевищувати р=16*10⁶Па. За рівнянням Клапейрона - Менделєєва.

,

Звідки

.

Підставивши числові дані, знайдемо

Відповідь: Найбільший об'єм балона має бути 0,0304 м .

 

Задача №3.

Визначити середню квадратичну швидкість молекул газу, густина якого при тиску р=50кПа становить ρ=4.1*10^-2кг/м³ .

 

Дано:   СІ

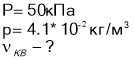
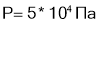
Розв'язування. За основним рівнянням молекулярне-кінетичної теорії для тиску маємо

де - n₀ число молекул в одиниці об'єму, m - маса молекули.

Добуток mn₀=ρ - це густина газу. Тоді,

;  

Тепер визначимо шукану величину;

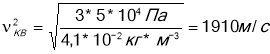
Відповідь: Середня квадратична швидкість молекул газу дорівнює 1910м/с.

 

Задача №4.

Газ, який займає об'єм 20л за нормальних умов, було ізобарно нагріто до 80°С. Визначити роботу розширення газу.

 

Дано:   СІ

 

 

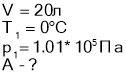
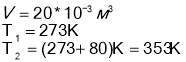
Розв'язування. Роботу розширення газу в ізобарному процесі визначаємо за формулою(2.9) . З рівняння стану газу випливає

Зрівняння Клапейрона-Менделєєва знаходимо число молів газу:

 

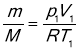
Звідки

Робота розширення газу

Відповідь: Робота розширення газу дорівнює 590 Дж.

 

 

 

 

 

 

Задача №5.

 

Температура нагрівника ідеальної теплової машини 500 К, температура холодильника 400 К. Визначити ККД циклу Карно і корисну потужність машини, якщо нагрівник передає їй 1675 Дж теплоти за секунду

Дано:

 

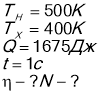
Розв'язування. ККД машини визначаємо за формулою:

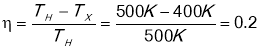
У корисну роботу перетворюються

Корисна потужність машини

Відповідь: ККД циклу Карно дорівнює 20%, а корисна потужність машини 335 Вт.

 

 

Задача №6.

У калориметрі  змішують три рідини, які  хімічно взаємодіють, масою m₁=1кг; m₂=10кг; m₃=5кг, відповідно з температура 6, -40, 60°С і питомими теплоємностями 2000, 4000 і 2000 Дж/(кг*K) Визначити температуру θ суміші і кількість теплоти, потрібну для наступне нагрівання суміші до t=6⁰С.

Дано:     СІ

 

 

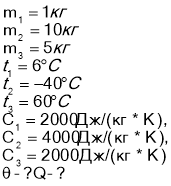
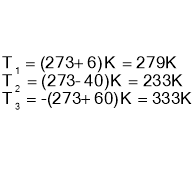
Розв'язування. З рівняння теплового балансу випливає, що алгебраїчна сума одержаних і відданих рідинами кількостей теплоти дорівнює нулю:

Розв'язавши це рівняння відносно θ, маємо

.

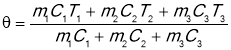Підставимо числові значення:

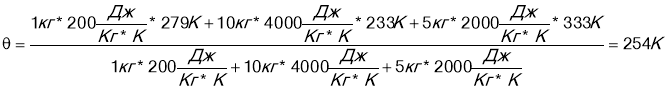 Щоб суміш нагріти до температури Т, потрібна кількість теплоти

Обчислимо цю величину:

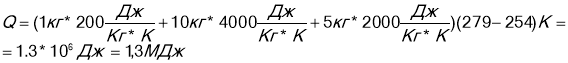
Відповідь: Температура суміші дорівнює 254 К, а кількість теплоти 1,3 МДж.

 

Задача №7.

Котел об'ємом V=5м³ заповнили водою, маса якої m₁ =20 кг. і нагріли її до температури t=180°С. Знайти тиск і масу водяної пари в котлі. Густина насичуючої пари води при цій температурі ρ=5.05 кг/м .

Дано:    СІ

 

 

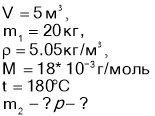
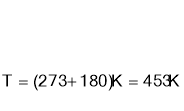
Розв'язування. Маса пари, потрібна для насичення котла об'ємом V при температурі Т,

 

Ми бачимо, що m>m₁, тобто вся вода в котлі перетвориться в пару, отже, m₁=m₂ і ця пара буде не насичуючою. Тиск не насичуючої пари визначаємо з рівняння стану

,

Звідки

 

Підставимо числові значення :

Відповідь: Тиск водяної пари в котлі дорівнює 840кПа, а маса 25,25 кг.

 

 

Задача №8.

Абсолютна вологість повітря при температурі t₁ =60⁰С дорівнює D₁=0.05 кг/м³. Знайти абсолютну вологість D₂ при зниженні температури дo t₂=10°С. Тиск насичуючої пари при температурі t₂ дорівнює 1226 Па.

Дано:    СІ

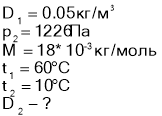
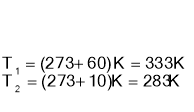
Розв'язування. Визначимо густину насичуючої пари при температурі Т^, виходячи з рівняння стану:

Оскільки , рівняння стану набере вигляду , звідки

Обчислимо густину :

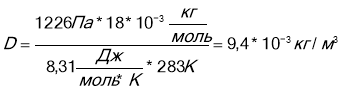
Густина насичуючої пари при температурі Т₂ менша від D₁, тобто D<D₁. Отже, при охолодженні до температури Т₂ частина пари сконденсується і абсолютна воло­гість повітря визначатиметься густиною насичуючої пари, тобто D₂=D=9.4*10^-3кг/м³

Відповідь: Абсолютна вологість повітря стала 9,4 *10^-3 кг/м³.

 

Задача №9

У посудину, яка містить 3 л води при 20°С, опустили кусок заліза масою 3 кг, нагрітий до 540°С. Від цього температура  вод підвищилась до 55°С і частина її випарувалась. Знайти масу води, яка перетворилась в пару.

Дано:     СІ

 

 

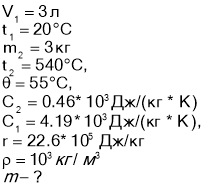
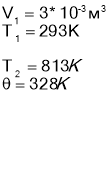
Розв'язування. Рівняння теплового балансу

Звідки

Підставивши числові значення і врахувавши, що маса , дістанемо

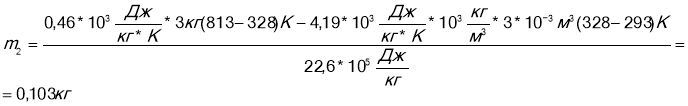 Відповідь: Маса води ,яка перетворилась в пару дорівнює 0,103 кг

 

 

Задача №10.

 

Дві пластини занурено в спирт. На скільки підніметься спирт, якщо відстань між пластинами зменшити з 1 до 0.5 мм? Змочування пластини вважати повним.

Дано:    СІ

 

 

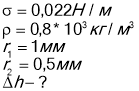
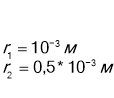
Розв'язування. Згідно з відомою формулою підняття рідини у капілярах

  

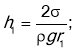
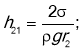
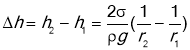
Зробимо обчислення:

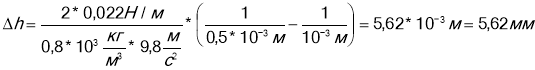
Відповідь: Спирт підніметься на 5,62 мм.

 

 

Задача №11.

 

Відносна вологість повітря вдень за температури 30°С становить 80%. Визначити масу роси, що випаде за ніч на землю, площею 100м² з шар повітря товщиною 2,0 м внаслідок його охолодження до 17°С. Тиск насиченої пари води за температури 17°С становить 1,94 кПа, а за 30°С - 4,2 кПа.

Розв'язання: У початковому стані водяна пара не насичена (В₁<1). З температури Т₁=(30+273)К парціальний тиск пари рівний р₁=В₁р_н1=3,39 кПа, а її парціальна густина ρ₁=Мр₁/(КТ₁)=24,2 г/м³. А з температури Т₂=(17+273)К порційний тиск насиченої пари ρ_н2=1,93кПа, а її парціальна густина р_н2=Мр₁/(КТ₂)=24,2г/м³ (густину насиченої пар визначаємо як густину ІГ). Оскільки ρ₁>ρ_н2 то під час зниження температур при Т=Т_р - точці роси (Т₂<Т_р<Т₁) пара досягне насичення (В_р=1)/ρ_нр=ρ₁.

За дальшого повільного охолодження повітря відбувається скраплення пари - випадання роси. При цьому відносна вологість В не змінюється залишаючись рівною одиниці, і в кінцевому стані, коли зниження температури припиниться, пара перебуватиме в стані ТДР, а її парціальний тиск: р₂=В₂р_н2=р_н2. Маса роси, роси, що випадає з повітря об'ємом V=Sh, дорівнюватиме m_h=m₁-m₂, так що маса при цьому об'ємі в кінцевому стані m₂=m₁-m_p, кількість речовини . Оскільки в початковому стані парa ненасичена , а в кінцевому вона перебуває у термодинамічній рівновазі рідиною (водою) на поверхні Землі, то в цих станах її можна вважати ІГ застосовувати до неї РМК.

 

 

 

ТПД, що відбувається з паром в процесі зниження температури, зобразимо схематично:

 

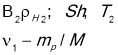
1. Згідно з РМК для водяної пари, яка є в повітрі за температур Т₁ і Т₂, можна записати:

2. Знаходимо m_p: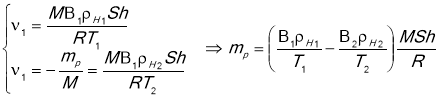

3. Одиниці; обчислення: [m_p] = 1кг; {m_p} = 1,95.

4. Із шару повітря площею 100м² і товщиною 2,0м внаслідок зниження температури від 30°С до 17°С на поверхню Землі випадає роса масою 1,95кг,

До речі, точка роси в даному випадку дорівнює 26°С, оскільки на цієї температурі дорівнює ρ_нр=ρ₁=24,4 г/м³; парціальна густина пари в інтервалі температур не змінювалася. Зауважимо, що як видно з таблиць, p_нр=p₁=3.36кПа р₁ (р₁=3,39 кПа); зниження температури насичене пари на кілька десятків кельвінів (градусів Цельсія) на її парціальний тиск практично не впливає, оскільки згідно з РМК за відсутності нескомпонентованого пароутворення (конденсації) відносна зміна тиску пари Таким чином, при знаходженні Т_р в інтервалі температур 0 - 30 К, характерному для нашого клімату, умова p_нр=p₁ y багатьох випадках з достатньою точністю може бути замінена умовою р_нр=р₁, де ρ₁ і ρ₂ стосуються денної температури, а ρ_н і р_н - нічної.

 

Задачі

 

1.     Знайти масу т сірчаного газу (S O₂), який займає об’єм V= 25 л при температурі 27 ⁰С та тиску P=100 кПа. (т=65 г)
2.     В балоні міститься маса т₁=10 кг газу при P₁=10 МПа. Яку масу т  газу взяли балону, якщо тиск знизився до P₂=2.5 МПа? Температура газа  залишилася незмінною. ( т=7.5 кг)
3.     Деякий газ при температурі t=10 ⁰С і тиск Р= 200 кПа має густину р=0.34 кг/м³. Знайти молярну масу газу. (= 0.004 кг/ моль)
4.     Маса т=12 г газу міститься  в об’ємі V₁= 4 л при температурі t₁=7 ⁰С. Після нагрівання газу при постійному  тиску його густина дорівнює р= 0.6 кг/м³. До якої температури Т₂ нагріли газ? ( Т₂= =1400 К)
5.     Маса т=10 г кисню знаходиться при тиску P=304 кПа і температурі t₁ =10 ⁰С. Внаслідок  нагрівання при постійному тиску об’єм кисню збільшився до V₂= 10 л. Знайти об’єм V₁ газу, температуру t₂, густину р₁ та р₂ газу до та після збільшення  об’єму. (V₁= 2.4 л, Т₂= 1170 К,  р₁=4.14 кг/м³ , р₂=1 кг/м³)
6.     В посудині знаходиться маса т₁=14 г азоту  та маса т₂=9 г водню при температурі t=10 ⁰С та тиску P=1 МПа. Знайти  молярну масу суміші  та об’єм V посудини. ( =0.0046 кг/моль, V=11.7 л )
7.     В посудині знаходиться маса т₁=10 г вуглекислого газу та маса т₂=15 г азоту. Знайти густину р суміші при температурі t= 27 ⁰С та тиску Р=150кПа. (р=1.98 кг/м³)
8.     Яка  кількість  молекул N знаходиться  в кімнаті об’ємом V=80 м³ при температурі t=17 ⁰С та тиску Р=1000 кПа? ( N=2х 10²⁷ )
9.     Молекула азоту летить з швидкістю v= 430 м/с. Знайти імпульс Р цієї молекули. ( Р=тv=2х 10^-23)
10. В посудині знаходиться  кількість v₁=10^-7 молей кисню та маса т₂= =10^-6 г азоту. Температура суміші t=100 ⁰С, тиск в посудині Р= =133 МПа. Знайти об’єм V посудини, парціальні тиски Р₁ та Р₂ кисню та азоту і кількість молекул n₀ в одиниці об’єму посудини. (V= =3.2 л, Р₁=98 кПа, Р₂=35 кПа, n₀=2.6х10¹⁹ м^-3 )
11. Знайти  кількість молекул n₀ водню в одиниці об’єму посудини при тиску Р=266.6 Па, якщо середня квадратична швидкість його молекул V_ск=2.4 км/с. (n₀ =4.2х10²⁴ м³)
12. Середня квадратична швидкість  молекул деякого газу при нормальних умовах V_ск=461 м/с. Яка кількість молекул n знаходиться в одиниці маси цього газу? (n=1.88х10²⁵ кг ^-1)
13. Знайти середню арифметичну, середню квадратичну та найбільшу  ймовірну швидкості молекул газу, який при тиску Р=40 кПа має густину р=0.3 кг/м³ . ( v=579 м/с, V_ск=628 м/с, v_йм=513 м/с)
14. При якій температурі  Т середня квадратична швидкість молекул азота  буде  більшою за найбільш ймовірну на  v=50м/с? ( Т = =83 К)
15. Яка доля молекули азоту при температурі t=150 ⁰С має швидкості v від 300 до 325 м/с? (N/n=2.8%)
16. Визначити середню квадратичну швидкість молекул кисню при 20 ⁰С. При якій температурі швидкість дорівнюватиме 500 м/с? (  480 м/с, 320 К)
17.  Знайти внутрішню енергію U маси т=20 г кисню при t=10 ⁰С. Яка частина цієї енергії припадає  на долю  поступального руху молекул та яка частина –на долю обертального? (U=2.7 кДж, U_пост.=2.2 кДж, U_об= 1.5 кДж)
18.  Енергія поступального руху молекул азоту, що знаходяться в балоні  об’ємом  V=20 л, U_пост.= 5кДж, а середня квадратична швидкість  його  молекул U_с.к.= 2х10³ м/с. Знайти масу т азоту в балоні та тиск Р, під яким він знадиться. (т=2.5 г, Р=167кПа)
19. Двохатомний газ, маса якого т= 1 кг та густина р= 4 кг/м³, знаходиться під тиском р=80 кПа. Знайти енергію теплового руху U молекул газу в цих  умовах . (U=50 кДж)
20. Яка кількість молекул N двохатомного  газу знаходиться в об’єм V=10 см² при тиску Р=5.3 кПа та температурі t=27 ⁰С? Яку енергію теплового руху U мають ці молекули?
21. Питома теплоємність деякого двохатомного газу С^I_p= 14.7 кДж/кг К. Знайти молярну масу цього газу. (=2х10^-3 кг/моль)
22. Густина  деякого двохатомного  газу при нормальних  умовах р=1.43 кг/м³. Знайти питомі теплоємності С^I_v та С^I_р цього  газу.( С^I_v=620 Дж/кг К, С^I_р=910 Дж/кг К)
23. Маса m = 10г кисню знаходиться при тиску Р = 0,3МПа і температурі t=10⁰C. Після нагрівання при Р = const газ зайняв об’єм V₂ = 10л. Знайти кількість теплоти Q, отриману газом, та енергію теплового руху молекул газу U до та після нагрівання (Q = 7,5кДж, U₁ = 1,8кДж, U₂ = 7,6кДж).
24. В закритій посудині об’ємом V = 10л знаходиться повітря при тиску Р=0,1МПа. Яку кількість теплоти Q треба надати повітрю, що тиск в посудині збільшився в 5 разів? (Q = 10кДж).
25. Маcа m = 6,5г водню, що знаходиться при температурі t=27⁰C, збільшує свій об’єм вдвічі при P = const за рахунок надання тепла ззовні. Знайти роботу А розширення газу, збільшення U внутрішньої енергії газу та кількість теплоти Q, надану газу (А=8,1кДж, Q = 28,4кДж, U = 20,3кДж ).
26. В закритій посудині знаходиться маса m₁ = 20г азоту та маса m₂=32г кисню. Знайти збільшення U внутрішньої енергії суміші газів при охолоджені її на Т = 28К. (U  1кДж)
27. При ізометричному збільшенні об’єму азоту масою m = 10г, який знаходиться при температурі t =17⁰С, виконана робота А=860Дж. Як змінився тиск азоту при збільшенні об’єму? (2,72рази).
28. Робота деякого газу масою m =10г при ізотермічному збільшенні об’єму від V₁ до V₂ = 2V₁ дорівнює А = 575Дж. Знайти середню квадратичну швидкість молекул газу при цій температурі (V_с.к=500м/с).
29. До якої температури охолоджується повітря, яке знаходиться при температурі 0⁰С, якщо його об’єм адіабатна збільшується від V₁ до V₂ = 2V₁ ? (Т₂ = 207К).
30. Тиск  повітря в циліндрі двигуна внутрішнього згорання адіабатична змінюється від Р₁ = 1атм. До Р₂ = 35атм. Початкова температура повітря 40⁰С. Знайти температуру повітря наприкінці процесу (Т₂ = 865К).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Література

 

1. Гельфгат І.М. та ін. Збірник різнорівневих завдань для державної підсумкової атестації з фізики. – Харків: Гімназія. 2003. – 80с.
2. Гельфгат И. М., Генденштейн Л. Э., Кирик Л. А. 1001 задача по физике с ответами и решениями. – 7-е 1зд. – Харьков: „Гимназия”. 2002 – 351с., ил.
3. Кирик Л.А. Фізика. – 10кл. Різнорівневі самостійні та контрольні роботи. Харків: „Гімназія ”, 2002. – 192с.
4. Фізика. Тести. 7-11кл.: посібник/ Н.В.Татарчук.– К.: „Академія”, 2008.-440с.