Знайомство з комбінаторикою

Знайомство з комбінаторикою

Сьогоднішнє заняття присвячене комбінаториці – розділу математики про вибір і розташування об’єктів певної множини за деяким принципом та обрахунок всіх можливих елементів, що задовольняють умови, за якими вони обираються.   

Приклад 1: із цифр 0; 2 та 4 скласти всі можливі трицифрові числа. Цифри у записі чисел не можуть повторюватись.

 Розв’язання. Перед усім зауважимо, що трицифрове число не може починатись цифрою 0, а тому нас влаштують лише числа, перша цифра у яких 2 або 4. Нехай перша цифра 2, тоді дві інші можуть бути 0 та 4 або навпаки – 4 та 0. Якщо ж взяти першою цифрою 4, таким самим чином отримаємо ще два числа.

Відповідь: 204; 240; 402; 420.

 У комбінаториці важливим є саме впорядкований перебір. Тобто числа, що ми складаємо, потрібно перебирати послідовно, за певним принципом.

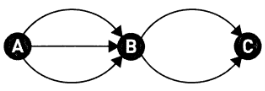
Приклад 2: у Країні чудес три міста, зазначені на схемі літерами А, В та С. Міста А та В з'єднані трьома дорогами, а міста В та С – двома. Скільки існує маршрутів для поїздки з А до С?

Розв’язання. Яку б дорогу з А до В ми не вибрали, у нас є два способи дістатись з В до С. Іншими словами, кожна дорога з А до С служить початковим етапом двох маршрутів з А до С. Отже, кількість маршрутів з А до С вдвічі більше за кількість доріг з А в В, а тому кількість таких маршрутів – це .

Відповідь: 6.

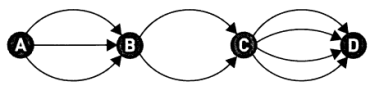
 Приклад 3: У Країні чудес побудували нове місто D і проклали чотири дороги з С до D. Скільки існує маршрутів для поїздки з А до D? Рухатися можна лише зліва направо.

Кількість маршрутів з А до С було обчислено у минулій задачі ().

Аналогічно маршрутів з А до D більше, ніж з А до С, у чотири рази, тобто .

Відповідь: 24.

На прикладі минулих двох задач можна зробити висновок: якщо ми обираємо певний елемент m способами і хочемо обрати ще один n способами, то ми це можемо зробити способами. Це комбінаторне правило множення у більш «дитячому» формулюванні.

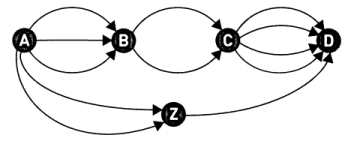
Приклад 4: У Країні чудес збудували ще одне нове місто (Z) та кілька нових доріг. Мапа доріг показана на наступному малюнку. Скільки тепер існує маршрутів для поїздки з А до D? (Правило залишається тим самим: рухатися можна лише у напрямку стрілок).

Розв’язання. Через міста В та С з А до D можна потрапити способами.

Або можна потрапити у місто D через місто Z ще 2 способами. Отже, маємо        способів.

Відповідь: 26

  У цій задачі можна помітити ще одну закономірність: якщо ми обираємо певний елемент m способами або можемо обрати його n способами, то ми це можемо зробити способами. Це, у свою чергу, є комбінаторним правилом додавання менш науковою мовою.

 Приклад 5: скільки існує різних 5-ти цифрових чисел, що складаються з цифр 2; 3; 6; 7 і 9? Цифри у записі чисел не можуть повторюватись.

Розв’язання. Складання всіх можливих чисел із даних цифр займе дуже багато часу, тому у даній задачі спробуємо інший підхід. На першому місці може стояти будь-яка із даних цифр, тобто у нас є 5 варіантів, на другому – на один менше (оскільки одна вже буде стояти на першому місці), тобто 4 варіанти. На трете місце лишається вже 3 варіанти, на четверте – 2, а на п’яте – 1. Оскільки ми хочемо обрати число, що має 5 розрядів (тобто ми вибираємо число на перше місце і друге і третє і четверте і п’яте), то можемо скористатись комбінаторним правилом множення: .

Відповідь: 120.

 Подібних задач, де потрібно переставляти елементи місцями, можна придумати багато. Всі вони будуть розв’язуватись подібним чином. Та і крім того таку «конструкцію» як добуток послідовних натуральних чисел від 1 до можна часто зустріти у математиці. Тому вона має свою назву – факторіал і своє окреме позначення ().   

Підбірка задач для самостійного розв’язання

1. Складіть всі можливі трицифрові числа, використовуючи числа 3; 7 та 8. Розмісіть ці числа у порядку зростання. На якому місці у цьому ряду стоїть число 783?  

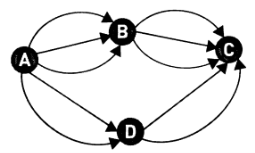
2. Чотири міста на острові Буяне з'єднані дорогами, як показано на малюнку. Скільки існує різних маршрутів з А до С? (Можна рухатися лише у напрямку стрілок).

3. У магазині чаю в Країні чудес продаються чайні чашки трьох видів, чайні ложки двох видів та чай чотирьох сортів. Скільки способами можна скласти подарунок з однієї чашки, однієї ложки та однієї пачки чаю?

4. У магазині кави в Країні чудес продаються чашки для кави п’яти видів, кава семи видів та турки двох видів. Скількома способами можна обрати подарунок, що містить одну чашку або одну пачку кави або однієї турки?

5. Мишко взяв із собою у літній табір дві пари черевиків, дві пари шортів та шість футболок. Скількома способами Мишко зможе одягнутися у таборі? (Комплект вбрання складається з пари шортів, футболки та пари однакових черевиків.)

6. Аліса взяла з собою у літній табір чотири пари туфель, дві спідниці, п'ять блуз і три сукні. Скількома способами Аліса може одягнутися у таборі? (Комплект одягу складається або з спідниці, блузки та пари однакових туфель, або з сукні та пари однакових туфель).

7. Белла прийшла з мамою до магазину іграшок, щоб вибрати Макс подарунок на день народження. У магазині є фігурки лицарів трьох видів, коней трьох видів та піратів двох видів, а ще є іграшковий корабель (одного виду). Мама дозволяє купити або лицаря і коня, або пірата та корабель. Скількома способами Белла може обрати подарунок для Макса?

8. Скількома способами можна обрати з 20-ти учнів старосту та заступника старости?

9. Скількома способами можна обрати з 20-ти учнів старосту та двох заступників старости?

10. Скількома способами можна обрати двох чергових у класі, де навчається 26 учнів? Пари чергових Олена-Петро і Петро-Олена вважайте однією парою.

11. Скількома способами можна скласти шестицифрове число з цифр 1; 2; 3; 4; 5; 6; 7? Цифри у записі числа не можуть повторюватись.

12. У класі навчається 25 учнів. Скількома способами можна скласти список список розсадки учнів у класі?

13. Скільки існує прямокутників із сторонами, що виражені цілим числом сантиметрів, площа яких дорівнює 30 см²?

14. Скільки існує прямокутників із сторонами, що виражені цілим числом сантиметрів, периметр яких дорівнює 16 см?  

15. Наталя має дві великі вази — одну з білими кульками, інша з чорними. Скільки способами вона може викласти чотири кульки в ряд? (Кожний спосіб - це певна послідовність кольорів. Якщо позначити білий колір буквою «Б», а чорний — буквою «Ч», то, наприклад, ЧЧЧЧ, БЧБЧ та ЧББЧ — різні способи).

16. Скільки різних слів можна одержати, використовуючи по одному разу всі букви слова «атом»? (Під «словом» мається на увазі довільну перестановку букв слова «атом»).

17. Скільки різних слів можна одержати, використовуючи по одному разу всі букви слова «атлас»?

18. Скільки різних слів можна одержати, використовуючи по одному разу всі букви слова «математика»?

19. Скільки існує трицифрових чисел, які при ділення на 9 дають остачу 2?

20. Скільки існує двоцифрових чисел, усі цифри у записі яких різні?

21. Скільки існує трицифрових чисел, усі цифри у записі яких різні?

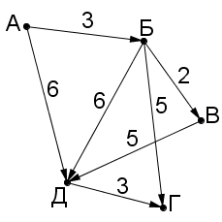
22. На рисунку зображено населені пункти А, Б, В, Г та Д, відстані між якими вказано на малюнку (у кілометрах). Скільки існує способів дістатися із міста А до міста Г? Який маршрут найкоротший?