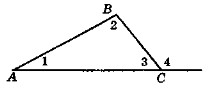
Зовнішній кут трикутника та його властивість

Конспект уроку: Зовнішній кут трикутника та  його властивість

Підготувала

вчитель математики

Петрівського Першого НВК

Боградського району Тарутинського ОТГ

Одеської області

Геометрія 7  за підручником Г.П.Бевз, В.Г. Бевз - 2016

Тема.  Зовнішній кут трикутника та  його властивість.

Мета: закріпити знання учнів про зміст теореми про суму кутів трикутника, а також про висновки з цієї теореми; засвоїти поняття зовнішнього кута трикутника та зміст теореми про градусну міру зовнішнього кута трикутника; сформувати вміння знаходити на рисунку і виконувати зображення зовнішнього кута трикутника при даній вершині трикутника; записувати теорему про градусну міру зовнішнього кута трикутника відповідно до умови задачі; використовувати властивість зовнішнього кута трикутника разом з теоремою про суму кутів трикутника для розв'язання задач, передбачених програмою.

Тип уроку: засвоєння і застосування знань, вироблення вмінь.

Обладнання: набір демонстраційного креслярського приладдя, таб­лиця  «Зовнішній кут трикутника».

Хід уроку

І. Організаційний етап   

ІІ. Перевірка домашнього завдання   

Перевірку засвоєння знань попереднього уроку проводимо у формі математичного диктанту

Математичний  диктант  

Варіант 1

1. Закінчіть речення «Сума кутів будь-якого трикутника дорівнює ...».
2. Чи існує трикутник з двома прямими кутами?
3. Чи існує трикутник, два кути якого дорівнюють від­повідно 120° і  80°?
4. Один із кутів трикутника тупий. Які два інших кути?
5. Чому дорівнює кут М трикутника МКО,  якщо кут К має градусну міру  70° , кут О — 30°?
6. У трикутнику ABC кут А у два рази більший за кут С, кут В в три рази більший за кут С. Якого виду трикут­ник ABC?

Варіант 2

1. Чи існує трикутник, два кути якого дорівнюють від­повідно 130° та 70°?
2. Чи існує трикутник з двома тупими кутами?
3. Закінчіть речення «Сума кутів будь-якого трикутника дорівнює ...».
4. Один із кутів трикутника прямий. Якими є два інші кути?
5. Чому дорівнює кут М трикутника МКО, якщо кут М дорівнює 110°, кут О дорівнює 30°?
6. У трикутнику ABC кут А на 20° менший від кута В, а кут С на 20° більший за кут В. Якого виду трикутник ABC?

Після диктанту обов'язково робимо корекцію — аналізує­мо помилки учнів, спираючись на відповідний навчальний матеріал.

III. Мотивація навчальної діяльності учнів. Формулювання мети і завдань уроку

Для створення відповідної мотивації діяльності учнів можна запропонувати їм виконати вправу.

Завдання  класу

1. Накресліть:

а) гострокутний трикутник ABC;

б) прямокутний трикутник ABC;

в) тупокутний трикутник ABC.

2. Проведіть промінь BD, доповняльний до променя ВА. Якими є кути ABC і DBC.
3. Виміряйте кути трикутника ABC і кут DBC. Порівняйте градусні міри кутів: DBC і ABC, DBC і суми А і С в ABC. Що ви помітили?

До виконаного завдання вчитель або учні формулюють такі запитання.

Запитання

1. Чи завжди можна побудувати кут DBC способом, опи­саним в умові задачі, і скільки таких кутів можна по­будувати при кожній вершині?
2. Чи буде співвідношення між кутом DBC і сумою кутів А і С, отримане при виконанні завдання «експерименталь­ним шляхом» загальною властивістю в будь-якому три­кутнику?
3. Пошук відповідей на поставлені запитання і становить ос­новну дидактичну мету уроку.

IV. Актуалізація опорних знань і вмінь учнів

Усні   вправи

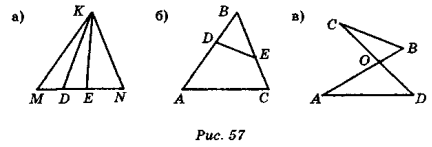
1. Знайдіть градусну міру кута х (рис. 56).

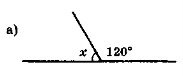
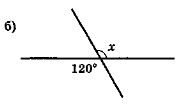
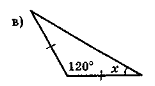
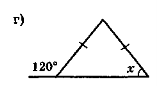
Рис. 56

2. Чи існує трикутник з двома:

а) тупими кутами;

б) прямими кутами?

3. Чи існує трикутник, усі кути якого:

а) гострі, менші від  60°;

б) гострі, більші за  60° ?

V. Засвоєння нових знань

План вивчення нового матеріалу

1. Означення зовнішнього кута трикутника.
2. Властивість зовнішнього кута трикутника.
3. Наслідок із властивості зовнішнього кута трикутника.

Методичний   коментар

Навчальний матеріал про зовнішній кут трикутника та його властивості в новому підручнику винесено в теоретичну частину § 10.

Уведення поняття зовнішнього кута трикутника підготов­лено виконанням практичної роботи, тому, давши означення зовнішнього кута, можна запропонувати кілька готових ри­сунків (як прикладів, так і контрприкладів) для закріплення розуміння означення.

На цьому етапі роботи важливо показати учням доціль­ність саме такої назви зовнішнього кута (як кута, що лежить зовні трикутника, на відміну від кута, або як ще говорять, внутрішнього кута, який лежить у внутрішній області три­кутника).

При цьому слід звернути увагу учнів на можливість по­будови двох рівних зовнішніх кутів трикутника при одній вершині.

Формулювання властивості зовнішнього кута трикутника також може бути результатом роботи з виконання завдання (див. вище); щодо доведення сформульованого твердження, то залежно від рівня підготовки учнів може бути організована або самостійна робота з текстом підручника або фронтальна бесіда під керівництвом учителя.

Також, якщо є час і за умови відповідної підготовки учнів, можна окремо виділити для вивчення наслідок з властивості зовнішнього кута трикутника — про те, що сума зовнішніх кутів трикутника, взятих по одному при кожній вершині, дорівнює 360° (загальна властивість зовнішніх кутів опуклого многокутника).

Підсумком проведеної роботи може бути таблиця «Зовнішній кут трикутника».

Таблиця

VI. Первинне усвідомлення матеріалу

Усні   вправи

1. Для трикутника ABC побудуйте зовнішні кути при вер­шині С.
2. Кут В трикутника ABC дорівнює 140°. Чому дорівнює зовнішній кут при вершині В?
3. Назвіть зовнішні кути:

а) при вершинах D і Е трикутника DKE (рис. 57, а);

б) при вершині Е трикутника KEN (рис. 57, а);

в) при вершинах D і Е трикутника DBE (рис. 57, б);

г) при вершині О трикутника AOD (рис. 57, в).

4. Обчисліть кут х (рис. 58) найраціональнішим спосо­бом.

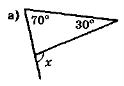
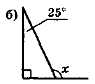
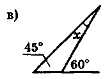
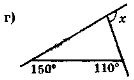
Рис. 58

Письмові   вправи

1. З підручника розв'язати вправи № 299, 306 (а, в), 307 (їх після доведення можна застосовувати як опорний факт при розв'язуванні задач).
2. Додатково: зовнішні кути трикутника відносяться як 3 : 4 : 5. Знайти внутрішні кути трикутника.

VII. Підсумки уроку

Для кутів трикутника MNK (рис. 59) записати якомога більше правильних рівностей.

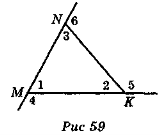
VIII. Домашнє завдання

1. § 10 (конспект уроку, с. 77, 78) — вивчити теорію.
2. Письмово: № 298, 306 (б, г).
3. Додаткові задачі.

1) Один із внутрішніх кутів трикутника дорівнює 40°, а один із зовнішніх кутів — 125°. Знайдіть решту внутрішніх та зовнішніх кутів трикутника.

2) Знайдіть внутрішні кути трикутника, якщо сума двох із них дорівнює 150°, а один із зовнішніх кутів дорівнює  80° .