Презентація "10 способів розв*язування квадратного рівняння"

Підготували учні 8 класу Йосипівського ліцею Новомиргородської міської ради Кіровоградської області Десять способів розв’язування квадратних рівнянь

Історики: «Ми захоплюємося давниною, але живемо сучасністю» Необхідність вирішувати рівняння в давнину була викликана потребою вирішувати завдання, пов'язані зі знаходженням площ земельних ділянок та земляними роботами військового характеру, а також з розвитком астрономії і самої математики.

Квадратні рівняння в Стародавньому Єгипті В папірусі, який знаходиться в Берлінському музеї зустрічається така задача: “Квадрат та інший квадрат, сторона якого є Ѕ+ј сторони першого квадрата, мають разом площу 100. Обчисли мені це.” Цю задачу можна розв’язати склавши рівняння хІ+ (Ѕ+ј)ІхІ = 100. Хід розв’язку самими єгиптянами зберігся не повністю, тому прослідкувати хід їх думок вченими не вдалось.

Квадратні рівняння Стародавнього Вавилону Вавилоняни вміли розв’язувати квадратні рівняння більше ніж 4000 р. тому. Правило розв’язків схожий на сучасний, але невідомо, яким чином вавилоняни дійшли до цього. Ось одна з вавилонських задач: “ Площа А, яка складається з суми двох квадратів, складає 1000, сторона одного з квадратів складає 2/3 сторони іншого, зменшені на 10. Які сторони квадратів?” (2/3х – 10)І + хІ =1000. В книзі записано простий хід розв’язування: “ Піднеси до квадрату 10, це дає 100, відніми 100 від 1000, це дає 900…” і т.д.

Квадратні рівняння в Стародавній Греції Математики Стародавньої Греції використовували для розв’язування лінійних і квадратних рівнянь метод прикладання площин. Прикладами таких задач є відшукання сторін правильних вписаних многокутників, яке називають “золотим перетином” відрізка. Метод розв’язку залежав від квадратного рівняння. Такі методи давали лише один додатній корінь. Стародавні математики розуміли необхідність так формулювати умову задач, щоб вони зазделегідь мали додатні розв’язки.

Квадратні рівняння в Стародавньому Китаї Починають зустрічатись в ІІІ ст. до н.е. Наведемо приклад з трактату “Математика в дев’яти книгах” (ІІ ст. до н.е.). “Маємо місто з межею у вигляді квадратів зі стороною невідомої величини, в центрі кожної сторони знаходяться ворота, на відстані 20 бу (1 бу = 1,6м) від північних воріт (за межами міста) стоїть стовп, якщо пройти від південних воріт 14 бу прямо, потім повернути на захід і пройти ще 1775 бу, то можна побачити стовп. Яка межа міста?” Розв’язком цієї задачі є відповідь 250 бу. І знову ж таки китайські вчені від’ємний варіант розв’язку рівнянь не розглядають.

Квадратні рівняння в Індії Задачі на квадратні рівняння зустрічаються в астрономічних трактатах “Аріабхатія”, у 492 р. індійським математиком і астрономом Аріабхатою. Інший індійський вчений Брахмагупта (VII ст.) виклав загальне правило розв’язування квадратних рівнянь. А ось одна з задач відомого індійського математика ХІІ ст. Бхаскари: “Розділившись на дві зграї забавлялись мавпи в гаї. Одна восьма їх в квадраті танцювали вельми раді. А дванадцять на деревах підняли веселий регіт, що навколо аж гуло. Скільки їх всього було?” І саме в розв’язанні Бхаскари помічаємо, що він знаходить два корені рівняння, отже він знав про двояку властивість кореня. (х/8)І+12 =х; хІ - 64х =- 768; хІ - 64х + 32І=-768 + =1024; (х-32)І=256; х=16 або х=48. Аріабхата Бхаскара

Квадратні рівняння в Середній Азії Середньоазіатський вчений аль-Хорезмі (ІХст.) в трактаті “Китаб альджерб валь-мукабала” отримав формулу коренів квадратного рівняння методом виділення повного квадрата за допомогою геометричної ілюстрації. Аль-Хорезмі

Квадратні рівняння в Європі Формули розв’язування квадратних рівнянь в Європі були вперше викладені в “Книзі абака”, яку написав у 1202р. італійський математик Леонардо Фібоначчі. Загальне правило розв’язування квадратних рівнянь, зведених до єдиного канонічного вигляду хІ+bх=с було сформульовано в Європі лише 1544 р. Штифелем. Вивід формули розв’язування квадратного рівняння в загальному вигляді зустрічається у Вієта, але він розглядав лише додатні корені. Лише завдяки працям Жирара, Декарта, Ньютона і ін. вчених спосіб розв’язування квадратних рівнянь приймає сучасний вигляд. Л. Фібоначчі Альбер Жирар

Франсуа Вієт (1540-1603) Народився на півдні Франції. Закінчив юридичну школу. Спочатку був адвокатом, а потім радником французьких королів. Весь свій вільний час віддавав заняттям з математики, а найбільше - алгебрі. Особливо пишався Вієт відомою теоремою про залежність між коренями квадратного рівняння та його коефіцієнтами, яку він отримав сам. Теорему було оприлюд-нено 1591 року. Її названо ім'ям Вієта, а сам автор формулював її так: «Якщо B+D, помножене на А, мінус А в квадраті дорівнює BD, то А дорівнює В і дорівнює D». Теорема Вієта стала зараз одним з найвідоміших тверджень шкільної алгебри. Франсуа Вієт

Група «Теоретики» Розум людський має три ключі, які все відкривають: знання, думку, уяву.

Означення Квадратним або рівнянням другого степеня з однією змінною називають рівняння виду ax2+bx+c=0, де x - змінна, а a,b,c - коефіцієнти квадратного рівняння, причому a≠0 .  Наприклад, x2-x-2=0 ; x2-3x-4=0; 7x2+4x-56=0.

Формула дискримінанту та коренів квадратного рівняння Дискримінантом називають значення підкореневого виразу

Випадки: 1) D>0,  то рівняння має два дійсні корені, які обчислюють за формулою 2) D=0 квадратне рівняння має один розв'язок (два співпадаючих корені) 3) D<0 рівняння дійсних коренів немає

Наприклад

Теорема Вієта Нехай x1,x2 - корені рівняння. Побудуємо на їх основі квадратне рівняння виду Якщо маємо квадратне рівняння вигляду , то сума його коренів рівна коефіцієнту p, взятому з протилежним знаком, а добуток коренів рівняння рівний вільному доданку q.

Наприклад Знайти корені рівняння х2 + 3х — 4 = 0. Розв’язання: визначаємо якими будуть сума та добуток коренів з умови рівняння х1 + х2 = —3, х1 х2 = —4. Шляхом підбору знаходимо, х1 =1, а х2 = - 4. Відповідь: 1 і – 4. Примітка. Якщо, в класичному рівнянні константа а відмінна від нуля, то потрібно поділити на неї все рівняння, а потім застосовувати теорему Вієта.

Група «Практики» Розум полягає не тільки в знанні, але й в умінні застосовувати знання на ділі.

Десять способів розв’язування квадратних рівнянь

1. Розкладання на множники лівої частини рівняння Мета: звести квадратне рівняння загального вигляду до виду А(х)·В(х)=0, де А(х) і В(х) – многочлени відносно х. Способи: - винесення спільного множника а дужки; - використання формул скороченого множення; - спосіб групування. Наприклад, x2 +10х - 24 = 0. Розкладемо ліву частина на множники: x2 +10х - 24 = x2 +12х -2х - 24 =х(х + 12) -2(х + 12) = =(x +12)(х - 2). Відповідь. -12 і 2.

2. Метод виділення повного квадрата Розв’яжемо рівняння x2 +6х - 7 = 0. Застосовуючи формули скороченого множення, маємо: x2 +6х - 7 = x2 + 2• x • 3 + 32 - 32 - 7 = =(x + 3)2 - 9 - 7 = (x + 3)2 - 16. Отже, дане рівняння можна записати так: (x + 3)2 - 16 =0, (x + 3)2 = 16. Тобто, x + 3 - 4 = 0, x1 = 1, чи x + 3 = -4, x2 = -7. Відповідь. 1 і -7.

3. Розв’язування квадратних рівнянь за формулою

4. Розв’язування квадратних рівнянь за допомогою теореми Вієта Для рівняння x2 + px +  q = 0 при а =1  маємо x1 x2 = q та x1 + x2 = - p, де x1 , x2 - корені рівняння. Наприклад, x2 + 4x – 5 = 0; x1 = - 5 і x2 = 1; x2 – 8x – 9 = 0; x1 = 9 і x2 = - 1.

5. Властивості коефіцієнтів квадратного рівняння

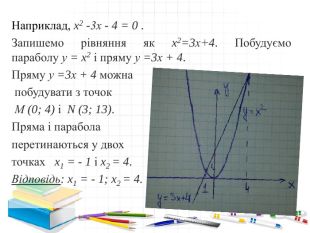
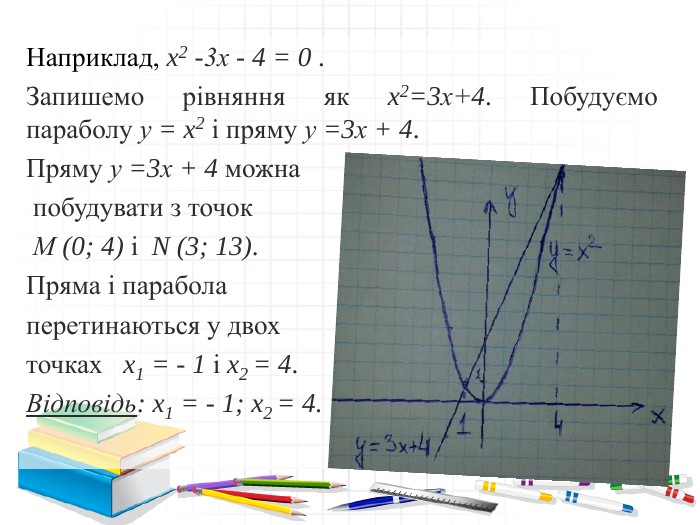
6. Графічне розв’язування квадратних рівнянь Рівняння x2 + px + q = 0 перепишемо у вигляді x2 = - px - q. Побудуємо графіки залежності у = x2 і у = -px -q.  Графік першої залежності - парабола, що проходить через початок координат. Графік другої залежності - пряма . Можливі такі випадки: - пряма і парабола можуть перетинатися у двох точках, то рівняння має два кореня; - пряма і парабола можуть перетинатися в одній точці, то рівняння має один корінь; - пряма і парабола не перетинаються, то квадратне рівняння немає коренів.

Наприклад, x2 -3х - 4 = 0 . Запишемо рівняння як x2=3х+4. Побудуємо параболу у = x2 і пряму у =3х + 4. Пряму у =3х + 4 можна побудувати з точок  М (0; 4) і N (3; 13). Пряма і парабола перетинаються у двох точках x1 = - 1 і x2 = 4.  Відповідь: x1 = - 1; x2 = 4.

7. Розв’язування квадратних рівнянь способом «перекидання»

У цьому способі коефіцієнт а  збільшує вільний член, ніби «перекидається» до нього, тому й називають способом «перекидання». Такий спосіб застосовують, коли можна легко знайти корінь рівняння, використовуючи теорему Вієта і що найважливіше, коли дискримінант є точним квадратом. Наприклад. 2х2 –11х + 15 = 0. «Перекидаємо» коефіцієнт 2 до вільної члену, внаслідок одержимо нове рівняння виду у2 –11у + 30 = 0. Відповідно до теореми Вієта у1 = 5; у2 = 6  .   Повертаємося до початкового рівняння маємо: x1 = 5/2 ,   x1 = 2,5 і  x2 = 6/2 ,   x2 = 3. Відповідь: 2,5; 3.

8. Розв’язування квадратних рівнянь за допомогою лінійки і циркуля

Наприклад x2 -2х - 3 = 0  На системі координат відмічаємо точки А(0;1) і В(2, -3). На діаметрі АВ будуємо коло. Воно перетинає вісь ОХ у двох точках: x1 = - 1; x2 = 3. Відповідь: x1 = - 1; x2 = 3.

9. Розв’язування квадратних рівнянь за допомогою номограми  Це старий і незаслужено забутий спосіб розв'язання квадратних рівнянь, поміщений на с.83 (див. Брадис В.М. Четирехзначние математичні таблиці. - М., Просвітництво, 1990).

10. Геометричний спосіб розв'язування квадратних рівнянь У давнину, коли геометрія була розвинена краще, ніж алгебра, квадратні рівняння вирішували не алгебраїчно, а геометрично. Ось як робили це стародавні греки. Наприклад. у2 +6у - 16 = 0. Запишемо рівняння у вигляді у2 +6у = 16, або у2 +6у + 9 = 16 + 9. Вирази у2 +6у + 9 і 16 + 9 геометрично це один і той же квадрат, а початкове рівняння набуває вигляду  у2+6у - 16 + 9 - 9 = 0 . Звідки й одержуємо, що   у + 3 = ± 5, тобто  у1 = 2, у2 = - 8