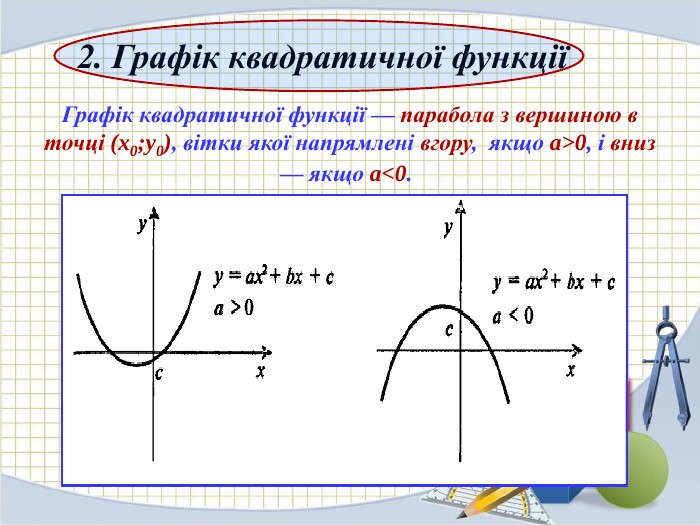
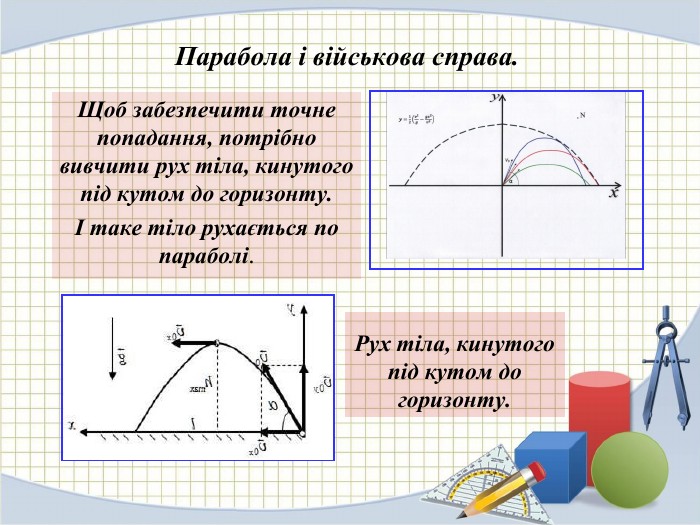
Квадратична функція.
Про матеріал
Матеріал можна використовувати при організаціії дистанційного навчання, індивідуального навчання в закладах освіти, окремі елементи можна використовувати на уроках при очній формі навчання. Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку