9 клас, презентація "Повторення та розширення відомостей про функцію""
Про матеріал
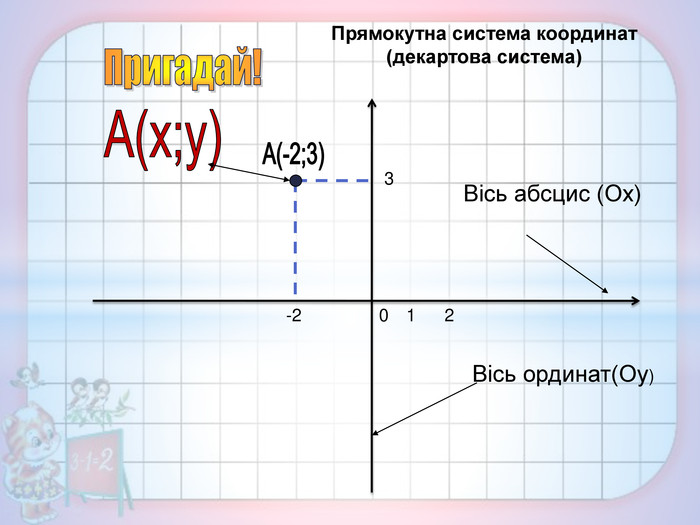
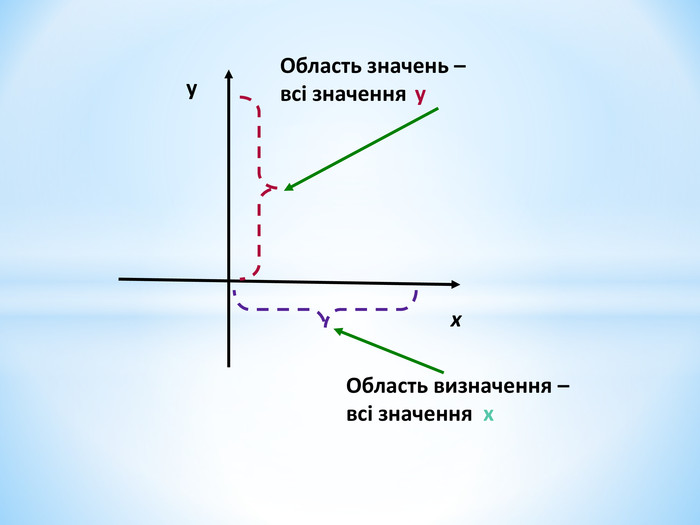
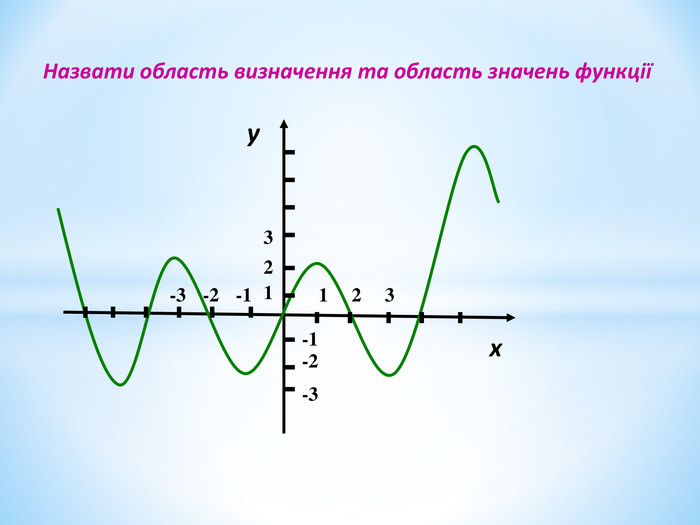
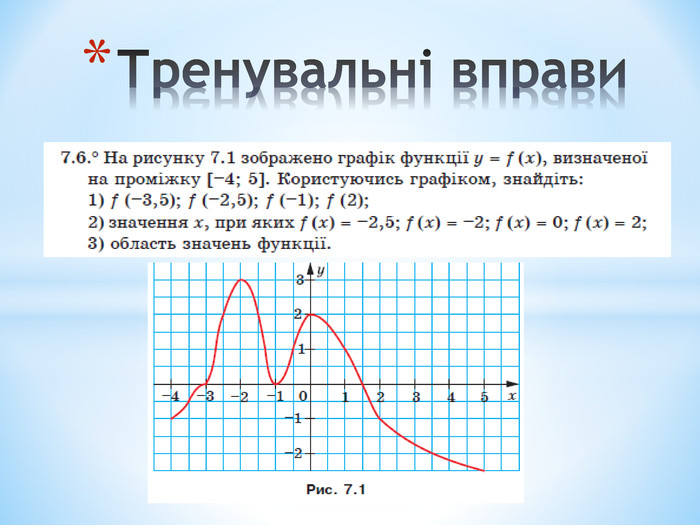
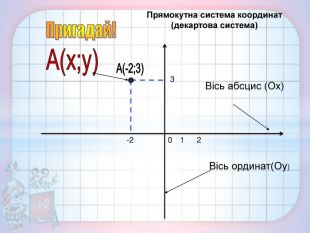
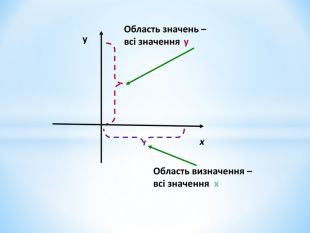
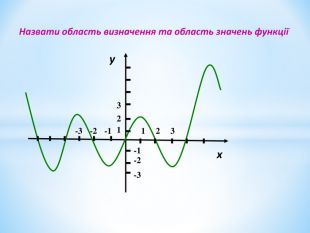
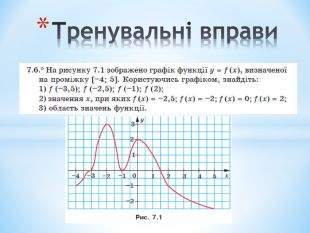
Презентація містить теоретичні та практичні завдання на актуалізацію опорних знань з даної теми, вивченої у 7 класі, та завдання на доповнення знань та формування вмінь. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
ppt
До підручника
Алгебра 9 клас (Мерзляк А. Г., Полонський В. Б., Якір М. С)
До уроку
7. Повторення та розширення відомостей про функцію Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку