Алгебра-інформатика. Похідна та її застосування
Предмет: Алгебра Вчитель: Околіта М. В.
Клас 11
Тема: Похідна та її застосування
Мета: удосконалити вміння та навички учнів розв’язувати задачі на застосування похідної; розвивати пізнавальний інтерес, навички роботи з тестами та логічне мислення.
Тип уроку: систематизація та удосконалення знань, умінь і навичок.
Обладнання: комп’ютерний клас, картки з тестами, рисунки з графіками функцій, програма-тренажер «Похідна» на комютерах.
Хід уроку
І. Організаційний етап.
- привітання;
- перевірка готовності учнів до уроку;
- налаштування на робочу обстановку;
ІІ. Мотивація навчальної діяльності. Оголошення теми та завдань уроку.
На минулих уроках ви засвоїли таке поняття, як «похідна». Це поняття з’явилося завдяки вченим:
- І.Ньютон,
- Г. Лейбніц,
- Ж. Ланграж,
- П.Ферма.
Похідна, як поняття ,застосовується у механіці, використовують також і у військовій справі, медицині ,фізиці і астрономії.
Тема нашого сьогоднішнього уроку – розв’язування вправ з використанням і застосуванням похідної. Мета уроку полягає у використанні теоретичних знань при розвязуванні практичних задач.
ІІІ. Актуалізація опорних знань.
А зараз ми пригадаємо, що ми вивчали на попередніх уроках, давши відповіді на декілька запитань.
1. Дати означення похідної?
(Число, яке дорівнює границі відношення приросту функції до відповідного приросту аргументу за умови, що приріст аргументу прямує до нуля)
2.Ознака зростання функції
(Якщо для всіх x з деякого проміжку f`(x) > 0 то функція зростає на цьому проміжку)
3. Ознака спадання функції
(Якщо для всіх x з деякого проміжку f`(x) < 0 то функція спадає на цьому проміжки)
4. Назвіть ознаку точки максимуму функції
(Якщо при переході через точку x0 похідна змінює знак з плюса на мінус, то x0 – точка максимуму)
5. Ознака точки мінімуму функції
(Якщо при переході через точку x0 похідна змінює знак з мінуса на плюс, то x0 – точка мінімуму)
Виконайте співвідношення відповідно до твердження
А)Функція зростає на [-6;1] і [3;9] значить вона зростає на [-6;9]
Б)Критична точка є точкою екстремуму.
В)Точка екстремуму є критичною
Г)Точки на графіку x1=1, x2=-1, x3 = 2 є точками максимуму.(на дошці зображено графік)
1) так, 2) ні, 3) так, 4) ні, 5)ні
IV. Застосування вмінь та навичок.
Всі учні, які присутні на уроці діляться на дві групи.
Перша група учнів проходить тестування на комп’ютерах в програмі-тренажері «Похідна». Після виконання тесту, програма автоматично виставляє оцінки за 12-бальною системою.
Друга підгрупа виконує тести на роздаткових картках.
-
Розв’язати рівняння y’=0, якщо
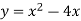
- -2
- -4
- 2
- 4
-
Знайти критичну точку функції
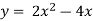
- -1
- 1
- 0
- 2
-
Знайти проміжок зростання функції
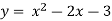
- (∞; 1)
- (1; ∞ )
- (-1; 1)
- (0; ∞)
- Розв’язати нерівність y’2
- (-∞;∞)
- (-∞; 5)
- (5; ∞)
- (-5; ∞)
Звіряємо свої відповіді з правильними:
1 – с)
2 – b)
3 – b)
4 – c)
Психологічна хвилинка
Підберіть до графіків функцій, які ви бачите перед собою, прислів’я, які на вашу думку імпонують цим функціям.
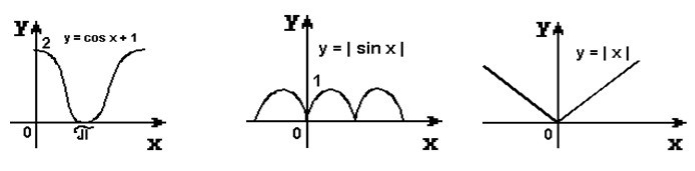
|
|
|
|
|
Любиш з гірки кататись, люби й санчата возити |
Повторення – мати навчання. |
Як крикнеться, так і відгукнеться |
V. Підсумок уроку
«Закінчи речення»
Сьогодні на уроці ми…
Найважливішим на уроці для мене було…
Найбільше зацікавило…
Найскладнішим для мене було…
VІ. Домашнє завдання
- Повторити таблицю похідних елементарних функцій.
- Підготувати повідомлення про відомих математиків, які зробили значний внесок у розвиток поняття похідної.
- Виконати у тесті № 1 «Перевір себе» завдання № 1-18 на стор. 150-152 (Г.П.Бевз, В.Г.Бевз. Математика, 11 – К., Генеза, 2011)


про публікацію авторської розробки
Додати розробку
