Арифметична прогресія
АРИФМЕТИЧНА ПРОГРЕСІЯ
Урок 2 Жодна інша наука не навчає так ясно розуміти гармонію природи,
як математика.
Прогресії- частинні види п о с л і д о в н о с т е й – зустрічаються в пам’ятках ІІ тисячоліття до н.е. А саме, як в клинописних таблицях в а в і л о н я н , т а к і в єгипетських папірусах (ІІ тисячоліття до н.е.)
Перші задачі на прогресії пов’язані із запитами господарського життя та громадської практики, наприклад, розподіл продуктів, поділ спадщини тощо.
Слово «прогресія» латинського походження
(progressio) означає «рух вперед», і вперше зустрічається у римського автора
Боеція (V – VI ст.).
П. Карус
 Розглянемо числову послідовність, перший член якої дорівнює 2,
а кожний наступний, починаючи з другого, дорівнює попередньому, доданому до числа 4: +4 +4 +4 +4 +4
Розглянемо числову послідовність, перший член якої дорівнює 2,
а кожний наступний, починаючи з другого, дорівнює попередньому, доданому до числа 4: +4 +4 +4 +4 +4
![]()
2; 6; 10; 14; 18; 22; … .
АРИФМЕТИЧНА ПРОГРЕСІЯ
|
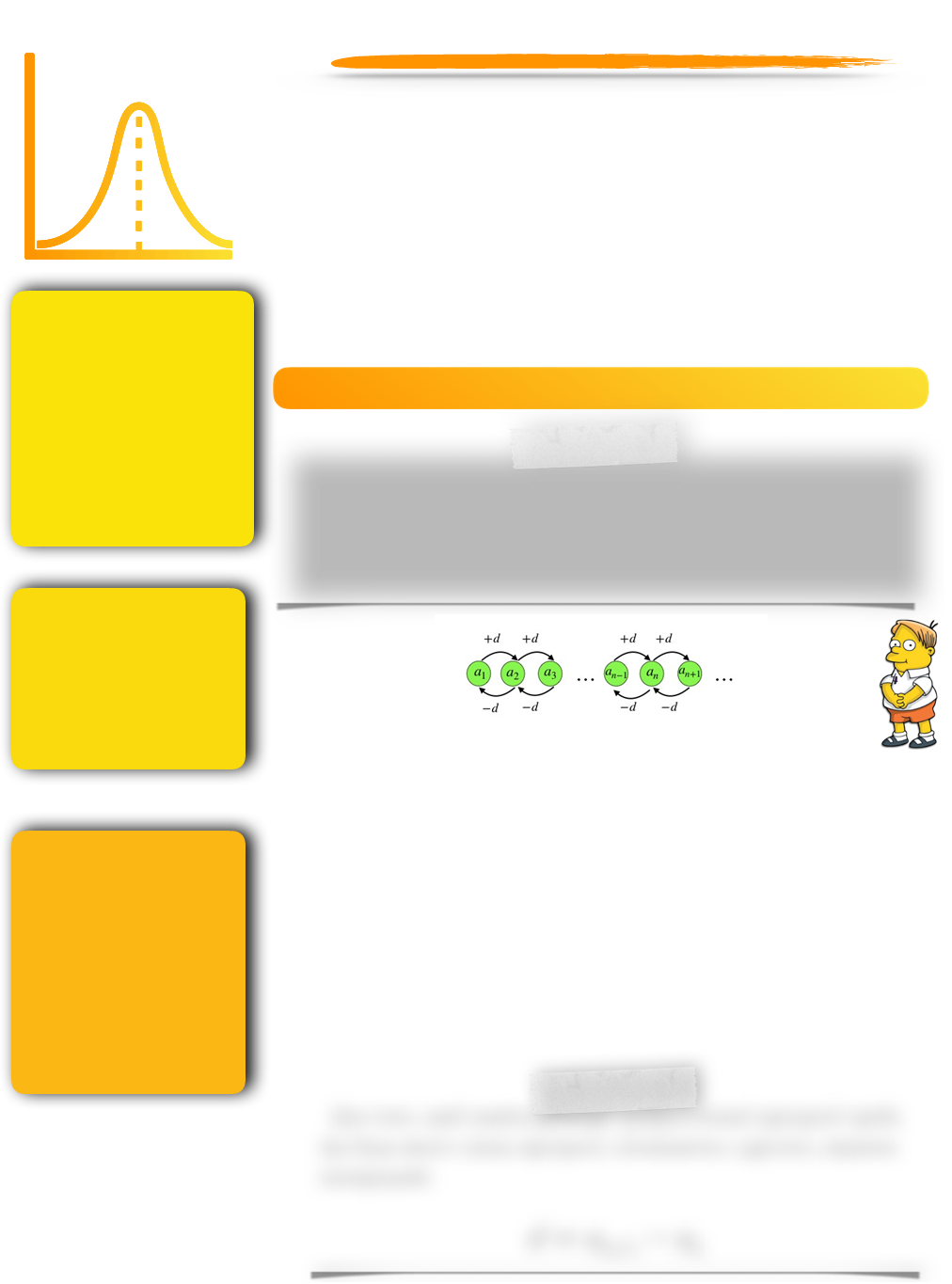
Таку послідовність називають арифметичною прогресією. Тобто, послідовність, кожен член якої, починаючи з другого, дорівнює попередньому, доданому до одного й того самого числа - це арифметична прогресія. |
a1;a2;a3;...;an−1;an;an+1;... - члени арифметичної прогресії;
d - це різниця арифметичної прогресії.
Тому, якщо (a n) - це арифметична прогресія, то виконуються рівності:
a 2 = a1 + d,a3 = a2 + d,a4 = a3 + d,...
Отже, для будь-якого натурального n справджується рівність: a n +1 =an+d
Для того, щоб знайти різницю арифметичної прогресії треба від будь-якого члена прогресії, починаючи з другого, відняти попередній:
d =an+1−an
 |
Приклад 3
Чи належить арифметичній прогресії 7; 10; 13; … число 102? Розв’язання:
У нашій прогресії a 1 = 7,a2 = 10, тоді d = a2−a1 = 10 − 7 = 3.
Складемо формулу n-го члена для даної прогресії:
a n = 7 + 3(n− 1) = 7 + 3n− 3 = 3n + 4, тобто an = 3n + 4.
Припустимо, що 102 - це якийсь член нашої прогресії, тоді існує
таке натуральне n, що an = 102, тобто 3 n + 4 = 102.
Розв’яжемо рівняння: 3 n + 4 = 102
3n = 102 − 4 3n = 98 n = 98 : 3 n = 322/3.

 |
 |
||
Отже, 32 2/3- це не натуральне число, тому 102 не є членом нашої послідовності. Відповідь: Ні.

1. Яку послідовність називають арифметичною прогресією?
2. Яке число називають різницею арифметичної прогресії?.
3. Як можна знайти різницю арифметичної прогресії?
4. Запишіть формулу n-го члена арифметичної прогресії.


про публікацію авторської розробки
Додати розробку
