Авторська програма "У світі математики"

У СВІТІ МАТЕМАТИКИ

Авторська програма гуртка «Кмітливі і допитливі»

 для 6 класу

Сухомаячківський заклад загальної середньої освіти І-ІІІ ступенів

Трохименко Любов Іллівна

вчитель математики, учитель вищої

кваліфікаційної категорії

Програма «У світі математики» створена автором для конкретної школи з урахуванням потреб і можливостей учнів.

Зміст авторської програми сприяє формуванню математичного способу мислення, розвитку творчого потенціалу школярів, здібностей до плідної розумової діяльності.

Матеріали програми можуть бути використані в роботі вчителів математики, керівників гуртків відповідного профілю.

 (6  КЛАС)

Трохименко Л.І., учитель

математики Сухомаячківського закладу

загальної середньої освіти І-ІІІ ступенів

Полтавського району Полтавської області

Авторська програма гуртка для учнів в 6 класі

Програму створено автором для конкретної школи з урахуванням потреб і можливостей учнів. Матеріали програми можуть бути використані в роботі вчителів математики, керівників гуртків, відповідного профілю як такі, що сприяють формуванню математичного способу мислення і розвитку творчого потенціалу школярів, здібностей до плідної розумової діяльності.

ВСТУП

Позакласна робота з предмета є важливою складовою роботи сучасної школи та закладів позашкільної освіти, невід’ємною частиною процесу навчання математики, складного процесу впливу на свідомість і поведінку учнів, поглиблення та розширення їхніх знань і вмінь.

Найважливішою метою проведення позакласної роботи є розвиток інтересу до математики.

Останніми роками в математиці виникли нові напрямки, які мають не тільки практичне значення, а й великий пізнавальний інтерес. Оновлення змісту основного курсу математики покликало оновлення позакласних занять із математики.

Для того щоб активізувати позакласну роботу, вчителі постійно відшукують можливості для більш якісного викладання предмета, а ситуація з чотирма годинами математики на тиждень спонукає до таких пошуків ще більш інтенсивно.  Заняття гуртків для цього є досить зручною можливістю. У річному плані школи передбачено гурткову роботу з різних предметів. Проблема полягає у тому, що затверджених програм для викладання у гуртках недостатньо, зокрема з математики для учнів в 6 класі.

Математичний гурток – одна з найбільш дієвих і ефективних форм позакласної роботи. Основою гурткової роботи є принцип добровільності. У роботі гуртка беруть участь усі охочі. До учнів, які показують зовсім невисокі результати, необхідно більш уважно ставитися, намагатися закріпити й розвинути їх інтерес до математики, стежити, щоб робота була для них посильною. Головне – зберегти масовий характер гурткових занять, що є наслідком доступності відвідування засідань гуртка всіма охочими.

Гурткова робота не є дублюванням класних занять. До організації роботи гуртка корисно залучати учнів: доручати їм підготовку повідомлень із теми, підбір задач і вправ, підготовку довідок історичного характеру, виготовлення моделей, рисунків тощо. На засіданнях гуртка вчителеві бажано створити атмосферу вільного обміну думками й активної дискусії.

Основне завдання гуртка – за допомогою раціонально й ретельно підібраних завдань розкрити значення математики, силу її ідей і методів, сформувати математичний спосіб мислення.

 Роботу гуртка можна спрямувати на розширення світогляду школярів. Для цього можна ознайомити учнів із деякими фактами історії математики, цікавими розв’язаннями відомих задач, а також із нерозв’язаними проблемами математики.

 Для того щоб гуртківці не втратили інтересу до роботи, кожній темі доцільно присвячувати 2-3 заняття, використовувати завдання ігрового і практичного характеру, вправи на вимірювання, побудову тощо. Форми проведення засідань гуртка також треба обирати різноманітні. Нарівні з традиційними слід використовувати й активні та інтерактивні форми: мозковий штурм, математичний бій, карусель, марафон та інші.

Роботу гуртка спрямовано на розширення світогляду, розвиток творчих здібностей учнів, прищеплення навичок самостійної роботи, підвищення якості математичної підготовки учнів.

Заняття гуртка проводять протягом 1 години один раз на тиждень. Для школи такий формат цілком прийнятий.

Викладання за цією програмою потребує від учителя певних знань  із педагогіки та володіння технологією інтерактивного навчання. Тому в роботі розглянуто методичні рекомендації щодо проведення занять (додаток).

Поурочне планування розраховане на урок, що триває одну академічну годину.

ПОЯСНЮВАЛЬНА ЗАПИСКА

Запропонована програма гуртка має на меті сприяти розвитку творчого потенціалу школярів, здібностей до плідної розумової діяльності.

 Завдання програми:

• створити умови для плідної співпраці дорослого зі школярами та позитивний клімат такої взаємодії;
• розкрити  значення  математики, силу її ідей і методів;
• сформувати математичний спосіб мислення;
• ознайомити учнів із деякими фактами історії математики,цікавими розв’язаннями відомих задач, а також із нерозв’язаними проблемами математики;
• розширити світогляд дітей щодо вивчення біографій видатних математиків;
• сприяти розвитку творчих здібностей учнів;
• прищеплювати навички самостійної роботи ;
• підвищувати якість математичної підготовки учнів.

Реалізація поставлених завдань стає можливою за умови використання активних та інтерактивних форм навчання за оптимального поєднання з традиційними. Широко використовують такі методи і прийоми, як роботу в малих групах та парах, мозковий штурм, рольові ігри, дискусії, розв’язування проблемних і пізнавальних завдань, тренінгові вправи. Важливим елементом є самостійна індивідуальна робота дітей над домашнім завданням.

Для створення доброзичливої і комфортної атмосфери в групі педагог має володіти активними формами навчання, навичками активного слухання, вмінням організовувати дискусії, роботу в малих групах, застосовувати елементи психологічного тренінгу.

Контроль набутих знань, умінь  і навичок проводять методами підсумкової рефлексії та само оцінювання.

                                     Мета занять гуртка

• прищеплювати учням інтерес до математики;

• поглиблювати і розширювати знання учнів з математики;

• розвивати математичний кругозір, мислення, до­слідницькі вміння та навички школярів;

• організовувати інтелектуально-практичну дослід­ницьку діяльність учнів;

• формувати логічне та абстрактне мислення, пози­тивні якості особистості (відповідальність, добро­совісність, дисциплінованість, охайність, посидю-чість);

• виховувати вміння долати труднощі під час розв'язу­вання математичних задач, наполегливість та ініціативу.

Завдання занять гуртка

• розширення уявлень учнів про математику як фор­му опису та метод пізнання дійсності;

• розширення розуміння значимості математики для потреб життя;

Характеристика структури програми

Програма представлена у табличному вигляді. Пер­ша таблиця представляє розподіл навчального матеріалу за темами. Далі наведено зміст навчального матеріалу за темами та вимоги до на­вчальних досягнень учнів у результаті їх вивчення. У змісті вказано той навчальний матеріал, який має бути вивче­ний з тієї чи тієї теми. Вимоги до рівня навчальних до­сягнень учнів відображають рівень засвоєння навчаль­ного матеріалу.

Зміст навчального матеріалу структуровано за тема­ми з визначенням кількості годин на їх вивчення. Курс розрахований на 35 годин (у 6-ому класі).

Друга таблиця пропонує орієнтовне календарно-тематичне планування занять гуртка, що допоможе вчителю у до­цільному підборі та раціональному розподілі матеріалу згідно з темами занять гуртка.

Розподіл навчального часу

(6 клас)

6 клас

         35 годин

Вступ (2 год)

• Роль математичних задач.
• Класифікація задач.
• Формування культури розв’язування математичних задач.

Мета:

• ознайомити учнів з класифікацією математичних задач;
• формувати культуру розв’язання задач;
• ознайомити з алгоритмом розв’язання задачі.

Основні вимоги.

учні повинні вміти:

• визначати тип задач;
• використовувати теоретичні знання для розв’язання задач;
• застосовувати алгоритми розв’язання задач.

Тема 1

Старовинні міри довжини (2 год)

• розв’язування задач, що містять старовинні міри довжин;
• історичні повідомлення  про сучасні застосування старовинних мір довжини.

Мета:

• ознайомити учнів зі старовинними мірами довжини;
• ознайомити учнів з історією виникнення метричної системи мір;
• узагальнити знання про способи вимірювання;
• розвивати пізнавальний інтерес учнів.

Основні вимоги.

учні повинні вміти:

• розв’язувати задачі, що містять старовинні міри довжини;
• використовувати отримані знання про способи вимірювання;
• порівняти таблиці метричної системи мір і старовинних мір довжини.

Тема 2

Задачі «Арифметики» Магніцького (3 год)

• Леонтій Пилипович Магніцький – перший російський видатний педагог-математик;
• «Арифметика» Магніцького;
• правило «хибного припущення» в задачах Магніцького;
• математичні забави в «Арифметиці» Магніцького

Мета:

• ознайомити учнів із біографією Л.П. Магніцького;
• дати коротку характеристику його підручника «Арифметика»;
• ознайомити з правилом «хибного припущення» як  методом розв’язування задач на складання рівнянь;
• розглянути деякі математичні «забави» з підручника Магніцького;
• виховувати інтерес до історії математики;
• розвивати творче мислення, обчислювальні навички.

Основні вимоги.

учні повинні вміти:

• використовувати методи розв’язування задач «Арифметики» Магніцького ( правило «хибного припущення»)

Тема 3

Діофантові рівняння (2 год)

• Діофант Александрійський;
• невизначені рівняння;
• методи розв’язування невизначених рівнянь;
• задачі, що можна розв’язати за допомогою діофантових рівнянь;
• внесок Діофанта в математику.

Мета:

• розвивати логічне мислення учнів;
• формувати учня як особистість, здатної до самостійної, творчої особистості;
• розглянути задачі, що можна розв’язати за допомогою діофантових рівнянь.

Основні вимоги.

учні повинні вміти:

• використовувати пошукові методи при розв’язуванні діофантових рівнянь;
• оволодіти способами розв’язання найпростіших діофантових рівнянь.

Тема 4  

Задачі, які розв’язуються за допомогою рівнянь (2 год)

• розв’язування текстових задач;
• перше рівняння;
• стародавня єгипетська задача;
• давньоіндійська задача;
• стародавня російська задача;
• Мухаммед ібн Муса аль-Хорезмі.

Мета:

• формувати  вміння розв’язувати рівняння;
• продовжувати роботу над формуванням стійких обчислювальних навичок;
• сприяти формуванню вмінь складати рівняння до задачі;
• розвивати логічне мислення учнів;
• сприяти розумінню фактичного матеріалу;
• підвищувати математичну ерудицію;
• зацікавити математикою;
• розширювати кругозір учнів, ознайомлюючи їх з історією математики.

Основні вимоги.

учні повинні вміти:

• розв’язувати задачі за допомогою рівнянь;
• вибрати і позначити невідому величину;
• встановити зв’язки між даними величинами;
• подати решту невідомих величин через основну невідому.

Тема 5

Задачі на переправу (2 год)

• особливості умов задач на переправу;
• схема, яку використовують для запису ходу розв’язання задач на переправу;
• розв’язування задач на переправу.

Мета:

• ознайомити школярів з особливостями умов задач на переправу;
• ознайомити учнів зі схемою, яку використовують для запису ходу розв’язання задач на переправу;
• навчити учнів розв’язувати задачі на переправу.

Основні вимоги.

учні повинні вміти:

• розв’язувати задачі на переправу;
• розуміти з чим пов’язані особливості умов задач на переправу;
• використовувати схему для запису ходу розв’язання таких задач.

Тема 6

Задачі на рух (5 год)

• задачі на односторонній рух;
• задачі на рух в різних напрямах;
• задачі на зустрічний рух;
• задачі на рух за та проти течії.

Мета:

• активізувати загальні відомості учнів про рух, основні величини;
• формувати навички складання числових виразів до задач  на рух;
• використання формул для розв’язання задач;
• навчити схематично записувати умову задачі  у вигляді малюнку, схеми;
• знати співвідношення між одиницями вимірювання;
• уміти знайти швидкість руху, час руху, пройдену відстань;
• сприяти розвиткові логічного мислення та творчого підходу до розв’язання задач;

Основні вимоги.

учні повинні вміти:

• знати основні величини та їх одиниці вимірювання;
• записувати та використовувати формули;
• встановлювати залежності між величинами;
• схематично записувати умову задачі у вигляді малюнку, схеми.

Тема 7

Розрахункові задачі на відсотки  (5 год)

• розв’язування задач на відсотки;
• знаходження відсотків від числа та числа за відсотком;
• відсоткове відношення чисел;
• задачі на суміші та сплави.

Мета:

• повторити поняття відсотка;
• запис даного числа у вигляді відсотків і навпаки;
• узагальнити і систематизувати знання і вміння учнів розв’язувати задачі на відсотки;
• знаходити відсоток від числа;
• знаходити відсоткове відношення чисел.

Основні вимоги.

учні повинні вміти:

• знаходити відсоток від числа;
• знаходити відсоткове відношення чисел.

Тема 8

Задачі на розчини і сплави (3 год)

• основні типи задач на відсоткові розрахунки;
• задачі на розчини  і сплави;
• розв’язування задач на розчини і сплави за допомогою рівнянь.

Мета:

• повторити основні типи задач на відсоткові розрахунки;
• узагальнити і систематизувати знання і вміння учнів розв’язувати задачі на відсотки.

Основні вимоги.

учні повинні вміти:

• розв’язувати задачі на розчини і сплави;
• знаходити відсоток від числа;
• розв’язувати задачі на розчини і сплави за допомогою рівнянь.

Тема 9

«Лавинні задачі» (2 год)

• «Лавинні задачі»;
• розв’язування «лавинних задач».

Мета:

• навчити виконувати обчислення в зазначеному порядку, якими  б громіздкими вони не виявилися;
• навчити розв’язувати «лавинні» задачі, застосовуючи ефективний й ефектний прийом;
• навчити скорочувати і спрощувати, щоб розв’язання стало легким, простим.

Основні вимоги.

учні повинні вміти:

• виконувати обчислення в зазначеному порядку;
• змінювати порядок дій, виносити який-небудь множник за дужки, робити інші подібні найпростіші перетворення, що спираються на основні закони арифметики.

Тема 10

 Задачі судоку (2 год)

• магічні квадрати;
• історія виникнення японської гри судоку;
• судоку – цікава математична задача;
• найпростіші вправи судоку;
• розв’язок судоку;
• прийоми розв’язування судоку.

Мета:

• ознайомити школярів з японською грою судоку;
• розвивати в учнів своєрідну «просторову уяву»;
• навчити розв’язувати вправи судоку різних рівнів складності;
• навчити прийомам розв’язування судоку.

Основні вимоги.

учні повинні вміти:

• створювати судоку;
• розв’язувати судоку.

Тема 11

Видатні математики (3 год)

• Остроградський Михайло Васильович – визначний математик;
• Вороний Георгій Феодосійович – геній з українським серцем;
• Кравчук Михайло Пилипович – людина неабиякої ерудиції та культури.

Мета:

• ознайомити з історико-біографічним  матеріалом;
• сформувати пізнавальний інтерес учнів до вивчення математики;
• ознайомити з життям і науковою діяльністю видатних українських математиків;
• формувати в учнів почуття національної свідомості, патріотизму, гордості за співвітчизників.

Основні вимоги.

учні повинні вміти:

• знати біографії математиків;
• брати участь у науковій творчості;
• розуміти історію математики, внесок вітчизняних учених у її розвиток.

Тема 12

Підсумкове заняття (2 год)

Українські генії математики

Усний математичний журнал

• Остроградський Михайло Васильович;
• Вороний Георгій Феодосійович;
• Кравчук Михайло Пилипович.

Мета:

• сприяти зацікавленості предметом;
• підвищити загальну культуру;
• розширити світогляд;
• активізувати пізнавальну діяльність учнів;
• формувати уявлення про математику як невід’ємну частину загальнолюдської культури;
• узагальнити та систематизувати вивчення біографій видатних математиків.

Основні вимоги.

учні повинні вміти:

• знати знаменитих земляків;
• внесок українських геніїв математики у її розвиток.

Календарно-тематичне планування

МЕТОДИЧНІ РЕКОМЕНДАЦІЇ ЩОДО ПРОВЕДЕННЯ ЗАНЯТЬ

МАТЕМАТИЧНОГО ГУРТКА

Вступ

Роль задач у шкільному курсі математики

Мета:

Ознайомити учнів з роллю задач у курсі шкільної ма­тематики. Розглянути основні види задач прикладного змісту,їх класифікацію, методи розв'язування.

«Не махай на все рукою, не лінуйся, а учись. Бо чого навчишся в школі, знадобиться ще колись!»

У процесі навчання математики задачі виконують різноманітні функції. Навчальні математичні задачі є до­сить ефективним засобом засвоєння учнями понять та методів шкільного курсу математики зокрема і матема­тичних теорій взагалі. Задачам належить велика роль у розвитку математичного мислення учнів, у формуванні в них умінь і навичок щодо практичного застосування математики. Саме тому на розв'язання задач відводить­ся половина навчального часу уроків математики. Пра­вильна методика навчання розв'язання задач відіграє істотну роль у формуванні високого рівня математичних знань, умінь і навичок.

Яке ж значення математичних задач ?

їх кілька:

• Освітнє: розв'язуючи задачі, учень набуває знань, підвищує свою математичну освіту.

• Практичне: під час розв'язання математичних задач учні навчаються застосовувати математичні знання для практичних потреб, готуються до практичної діяльності в майбутньому, до розв'язання задач, що висуває практика та повсякденне життя. Математичні задачі розв'язують у фізиці, хімії, біології, географії, електро- та радіотехніці, особливо в їх теоретичних основах. Це означає, що в процесі навчання математики учні повинні розв'язувати за­дачі, пов'язані з суміжними навчальними предметами, а також задачі з практичним та технічним змістом.

• Розвиток мислення: розв'язуючи задачі, вчаться ана­лізувати: виділяти умову і висновки, дані і шукані вели­чини , знаходити спільне, порівнювати та протиставля­ти факти. В учнів при цьому формується особливий стиль мислення: збереження формально-логічної схеми мірку­вань, лаконічне висловлювання думок, чітка розчлено­ваність ходу мислення, точність символіки.

• Виховне значення математичних задач. Задача вихо­вує своїм текстовим змістом, тому текстовий зміст математичних задач істотно змінюється в різні періоди роз­витку суспільства. Сюжетний зміст задач, уміщених у су­часному підручнику, спрямовано на виховання в учнів високих моральних якостей, наукового світогляду. Вихо­вує також сам процес навчання розв'язування матема­тичних задач.

Пропонуючи розв'язання тієї чи тієї задачі, вчитель ставить на меті реалізувати певні цілі: педагогічну, ди­дактичну, навчальну.

Навчаюча ціль

а) Задачі для засвоєння математичних понять.

Формування математичних понять успішно прохо­дить за умови ретельної та копіткої роботи над поняття­ми, їх означеннями і властивостями.

б) Задачі для оволодіння математичною символікою.

1) Однією з цілей, що ставиться під час вивчення мате­матики навчити учнів -володіти математичною мовою і, отже, математичною символікою. Найпростіша символіка вводиться в початковій школі, в 5-6 класах (знаки дій, рівності та нерівності, дужки, знаки кута, паралельності, пер­пендикулярності прямих і т.д.), і користуємось нею весь час. Задачі для навчання доведенням.

Навчити доводити — одне з найголовніших завдань навчання математики. Найпростішими задачами такого змісту є задачі-запитання та  [елементарні задачі на дос­лідження]. Розв'язання таких задач полягає в [знаходженні відповіді на запитання і доведенні її істинності].

г) Задачі на формування математичних умінь і навичок.

- Ті, що передують вивченню нових математичних фактів: вони сприяють концентрації уваги учнів на ідеях, поняттях, методах математики, які знову вивчають:

- за допомогою яких вводять нові поняття і методи:

- ті що створюють проблемну ситуацію з метою фор­мування нових знань:

- розвиток мислення учнів у процесі розв'язання математичних задач.

Розв'язування задачі вимагає застосування багатьох ро­зумових дій: аналізувати задачу, задану ситуацію; порівню­вати дані і шукані, дану задачу, що розв'язується з тією, що була розв'язана раніше, встановлюючи приховані вла­стивості заданої ситуації; конструювати найпростіші ма­тематичні моделі, здійснюючи мислений експеримент; синтезувати, відбираючи корисну для розв'язання задачі інформацію, систематизуючи, коротко та чітко, у вигляді тексту, символічно та графічно, оформляти думки, об'єк­тивно оцінювати отримані результати.

Підбираючи задачі, потрібно враховувати такі критерії:

- задачі, що містять елемент дослідження;

- задачі на доведення;

- задачі на встановлення помилок;

- цікаві задачі;

- знаходження різних варіантів і вибір кращого з них;

-самостійне складання задач учнями. Розв'язання математичних задач виховує: ретельність, уважність, зосередженість, наполегливість у подоланні

труднощів, упертості в досягненні поставленої мети, ви­ховує почуття обов'язку та відповідальності.

Шляхом розв'язування задач учні навчаються матема­тики. Вони засвоюють велику кількість математичних по­нять, символіку, набувають навичок виконувати доведення.

Розв'язування математичних задач допомагає вико­нанню дидактичних цілей:

- підготовка до вивчення теоретичних питань мате­матики;

- закріплення тільки що набутих теоретичних знань:

- ілюстрація застосувань вивченого.

Задачі практичного змісту ілюструють застосування математики в техніці, побуті, суміжних навчальних пред­метах. Наприклад:

1. Визначення швидкості руху, часу чи відстані.

2. Визначення маси тіла.

3. Визначення масштабу, і т.д.

4. Формування вмінь.

5. Повторення раніше вивченого.

6. Контроль засвоєння математичних знань.

При організації роботи з розв'язування математич­них задач доцільно використовувати такі види діяльності:

- фронтальне розв'язування задач-розв'язання однієї і тієї ж задачі з всіма учнями класу в один і той же час:

- індивідуальне розв'язування задач: при індивіду­альному доборі задач враховують індивідуальні здібності та можливості учня.

Задачі практичного змісту виділяють прикладні ас­пекти математики. Вони сприяють виконанню багатьох завдань навчального процесу: розкривають методологічні питання взаємозв'язку теорії та практики; формують в учнів наукове світорозуміння; активізують пізнавальну діяльність учнів; підвищують інтерес до навчального предмета: забезпечують розвиток технічної творчості, здійснюють профорієнтаційну роботу.

Старовинні міри довжини

Пригадати, якими одиницями зручно вимірювати довжини відрізків, відстань між об’єктами. Як ці одиниці пов’язані між собою?

Ознайомитися з іншими мірами довжини, які були відомі задовго до того, як з’явилися метр, дециметр, сантиметр. Дізнаємося, як вимірювали в давнину.

Порівняти метричну і старовинну таблиці мір довжини.

Під час занять учні розв’язують задачі, що містять старовинні міри довжини.

Розв'язування задач, що містять старовинні міри довжини (тренувальні вправи)

1) Знайдіть зріст у міліметрах Дюймовочки з однойменної казки Андерсена.

2) У казці О. С. Пушкіна в царя Салтана наро­дився син «в аршин». Знайдіть зріст майбут­нього князя Гвідона в дюймах.

3) Морякам перед плаванням бажають «сім футів води під кілем». Знайдіть цю відстань у дециметрах.

4) Горщик має висоту дві п'яді. Знайдіть зріст у сантиметрах того, хто «від горшка два вершка» (мається на увазі вище на два вер­шка).

5) Про розумну людину кажуть: «У неї сім п'ядей у лобі». Чи можливо мати лоб такої висоти?

6) В одній приказці говориться: «П'ять верст до небес, і все лісом». Скільки метрів до «не­бес»?

7) Кільце баскетбольного кошика знаходиться на відстані 10 футів над землею. Знайдіть цю відстань у метрах, сантиметрах, міліме­трах.

8) Довжина футбольних воріт 7 м 44 см, а висо­та 2 м 48 см. Знайдіть розміри воріт у футах, якщо 1 фут _͌ 31 см.

Виконують практичні завдання.

Практикум

Учні класу об'єднуються в пари і виконують практичні завдання.

1) Виміряйте розміри парти в долонях, ліктях, п’ядях, футах.

2) Виміряйте свій зошит та щоденник у дюй­мах та вершках.

3) Виміряйте в ліктях та аршинах довжину тканини.

Мають місце історичні повідомлення про сучасне застосування старовинних мір довжини.

Історичні повідомлення про сучасне застосування старовинних мір довжини

(Групи учнів отримали це завдання заздале­гідь і мали змогу підготуватися.)

- Такі міри, як дюйм, сажень, лікоть, ар­шин, верста ми знаходимо в казках.

- Розміри автомобільних та велосипедних шин і зараз указують у дюймах.

- Діаметри водопровідних труб указують у дюймах.

- Розміри футбольних воріт 24x8 футів.

- Глибини морів та океанів на американ­ських та англійських картах указано у футах.

- Зріст людини в Англії та Америці вказу­ють у футах.

                     ТЛУМАЧНИЙ СЛОВНИЧОК ДЕЯКИХ МІР

Метр - від грецького «метрон» (палиця для вимірювання).

Дюйм - від голландського «дюім» (великий палець).

Фут - у перекладі з англійської означає «ступня».

Аршин - від персидського «арш» (лікоть).                                               

Сажень - від слова «саджати» (малося на увазі саджати молоді деревця).

                                             Міри довжини

1 верста = 1,07 кілометра

1 сажень = 2,13 метра

1 аршин = 71,12 сантиметра

1 вершок = 4,45 сантиметра        

1 фут = 30,48 сантиметра                                    

1 кілометр = 0,94 версти 

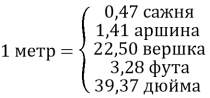
1 географічна миля = 6,96 версти = 7,42 кілометра

1 морська миля = 1,74 версти = 1,85 кілометра                                 

Задачі «Арифметики» Магніцького

Заняття гуртка розпочати вступним словом вчителя.

Вступне слово вчителя

З перших відомих письмових джерел ми дізнаємося, що математичні знання на Русі були розповсюджені уже в X-XI ст. Вони пов'язані з практичними потребами людей-літочислення, підрахунки поголів'я і вартості стада, визначення прибутку від збору врожаю тощо. У Х-ХІ ст. за часів Ярослава Мудрого було відкрито перші школи. Цілком можливо, що того часу могли з'явитися і перші навчальні посібники. Це так звані азбуковники - своє­рідні енциклопедичні словники, у яких, крім алфавіту і молитв, уміщували тлумачення дея­ких слів, правила моралі й поведінки, календар, початки арифметики тощо. Уже тоді виділялися «числолюбці», яких цікавила математика.

У XVI-XVII ст. починає з'являтися і розповсю­джуватися рукописна математична література.

Рукописи того часу відіграли значну роль у розповсюдженні математичних і практичних знань. Вони були тією основою, на якій ство­рювали навчальну літературу XVIII ст.

Перебудова державного, громадського і куль­турного життя країни, розпочата Петром І, вимагала великої кількості спеціалістів у різ­них галузях господарства. Для підготовки таких кадрів, для розповсюдження математичних знань виникла потреба в підручниках. 1703-го року підручник було видано у типографський спосіб нечувано великим для того часу накла­дом - у кількості 2400 екземплярів. Це була «Арифметика» Магніцького.

Ознайомити учнів із біографією Л.П.Магніцького. Дати коротку характеристику його підручника «Арифметика». Звернути увагу на те, що ця книга насправді була глибоко продуманою, оригінальною працею самого Магніцького і за методичними достоїнствами стояла вище за сучасні їй підруч­ники математики, поширені за кордоном.

Найважливішою особливістю цієї праці є пра­гнення не тільки догматично викласти основні правила й питання математики, але й роз'яснити їх на численних прикладах: весь виклад перейня­тий бажанням дати учневі розуміння практичного застосування досліджуваних питань.

Деякі методи розв'язування задач «Арифмети­ки» Магніцького корисно знати й сучасним шко­лярам. Наприклад, правило «хибного припущен­ня».

Діофантові рівняння

Програма з математики «забула» про діофантові рівняння, але вони зустрічаються на олімпіа­дах, різноманітних конкурсах, турнірах тощо. Тому ми вважаємо доцільним звернутися до цієї важливої та цікавої теми в позакласній роботі. Ця тема важлива ще й тому, що діофантові рівняння дають велику можливість для розвитку логічного мислення учнів, бо більшість таких рівнянь мож­на розв'язати, спираючись не на спеціальну тео­рію, а на здоровий глузд і кмітливість.

До кожного типу рівнянь треба підходити твор­чо, використовуючи пошукові методи, які в першу чергу спрямовані на формування учня як особис­тості, здатної до самостійної, творчої діяльності.

Метою цього заняття є:

• розглянути задачі, що можна розв’язати за допомогою діофантових рівнянь;
• оволодіти способами розв’язання найпростіших діофантових рівнянь.

На нашу думку, кожний учень здатний оволодіти способами розв’язання найпростіших діофантових рівнянь, якщо він має навички розв’язування звичайних (визначених) рівнянь.

Доцільним буде цікава інформація за цією темою.

Діофант Александрійський

Стародавні єгиптяни для зручності міркувань придумали спеціальне слово, яке означало неві­доме, але вони не мали знаків рівності й знаків дій (на зразок наших плюса, мінуса), тому запи­сувати рівняння вони не вміли. Перший крок у цьому напрямку зробив Діофант Александрійський (за назвою великого культурного, торго­вельного й наукового центру давнього світу - міста Александрії; це місто збереглося й на сьо­годні, знаходиться у Єгипті) - учений, який використовував досягнення єгиптян, вавилонян і греків. Про його життя майже немає відомос­тей. Припускають, що він жив у III ст. Основні події життя записано на його надгробку.

Прах Діофанта гробниця ховає:

Вдивися — і камінь

Мудрим мистецтвом розкриє покійного вік:

З волі богів шосту частину життя був він дитина,

А ще половину шостої — стрів із пушком на щоках.

Тільки минула сьома, з коханою він одружився,

З нею п'ять років проживши, сина діждався мудрець.

Та півжиття свого тішився батько лиш сином:

Рано могила дитину у батька забрала.

Років двічі по два батько оплакував сина.

А по роках цих і сам стрів він кінець свій печальний...

За часів Діофанта мовою науки була грецька. Але греки ще не знали цифр і позначали числа за допомогою букв свого алфавіту. Перші дев'ять букв: α (альфа), β (бета), γ (гамма), ... позна­чали числа від 1 до 9; наступні дев'ять: ι (йота), κ (каппа), ... позначали числа від 10 до 90; нарешті, наступні дев'ять: ρ (ро), σ (сигма), ... позначали числа від 100 до 900. Щоб не поми­литися і не прийняти число за слово, над бук­вами, що позначають число, ставили рисочку. Алфавіт нараховував 28 букв, одна з них була особливою (сигма кінцева): ставилася тільки в кінці слів і числового значення не мала. Ось нею Діофант і став позначати перший степінь невідомого, так само як ми зазвичай позначаємо його буквою х. Діофант Александрійський почав писати замість «дорівнює» знак «і», тобто букву «і» (скорочення слова «ізос» — рівний). Для віднімання Діофант застосовував букву ψ (псі), тільки перевернуту, скорочену й спроще­ну за формою. А без знака додавання Діофант обходився досить просто — доданки записував поруч один із одним.

Задачі, які розв’зуються за допомогою рівнянь

На цьому занятті розглянемо нескладні задачі, тобто розв’яжемо кілька стародавніх задач.

Задача 1. Стародавня єгипетська задача

Кількість та її чверть дорівнюють разом 15. Знайти кількість.

Розв'язання задачі 1. Нехай х — кількість, тоді її чверть — 0,25х. Отже, (х + 0,25х) — загальна кількість. За умовою ця кількість дорівнює 15, звідси маємо рівняння: х + 0,25х = 15, звідки х = 12.

Задача 2. Стародавня російська задача

Хтось запитав учителя: «Скільки маєш учнів, бо я бажаю віддати сина до тебе на навчан­ня». Учитель відповів: «Якщо до мене прийде учнів ще стільки ж, скільки маю, і півстільки, і чверть, і твій син, тоді буде в мене учнів 100». Скільки було в учителя учнів?

Задача 3. Стародавня російська задача

Летіла зграя гусей, а назустріч їм ще один. Гусак говорить: «Здрастуйте, сто гусей». А йому відповідають: «Нас не сто гусей, а менше. Якби нас було стільки, та ще стільки, та ще півстіль­ки, та ще чверть стільки, та ти, гусаче, тоді нас було б сто гусей». Скільки гусей було в зграї?

Розв'язання задач 2 і 3. Нехай в учителя х учнів, тоді кількість учнів, яку називав учитель, дорів­нює:

                                  (х+ х+0,5 х+ 0,25 х+1).

За умовою ця кількість дорівнює 100, звідси маємо рівняння:

                            х+ х+0,5 х+ 0,25 х+1=100, х=36.

Відповідь. 36 учнів.

Задачі на переправу

Особливості умов задач на переправу пов’язані з обмеженою вантажопідйомністю плавальних засобів, із кількістю й особливостями пасажирів.

Для запису ходу розв’язання таких задач використовують схему, яку складають у такий спосіб: схематично зображують річку, береги й плавальний засіб; кожний етап переправи відділяють горизонтальною рискою; напрямок руху плавального засобу вказують "стрілкою над позначенням тих, хто переправляється на поточ­ному етапі.

Задача 1. Батькові з двома синами потрібно на плоту переправитися через річку. Пліт ви­тримує на воді або батька, або двох синів. Як переправитися на другий берег батькові й си­нам? Скільки часу (мінімально) буде потрібно на переправу, якщо кожна поїздка через річку займає 3 хвилини?

Розв'язання. Порядок переправи на другий берег подано в таблиці (С₁ - перший син, С₂ - другий син, Б - батько).

                                                                                                                                                              Відповідь. На переправу потрібно 15 хвилин.

Задача 2. Селянинові потрібно перевезти через річку вовка, козу й капусту. Але човен такий, що в ньому може поміститися селянин або тіль­ки з вовком, або тільки з козою, або тільки з капустою. Якщо залишити вовка з козою наодинці, то вовк з'їсть козу, а якщо зали­шити козу одну з капустою, то коза з'їсть капусту. Як перевіз свій вантаж селянин?

Розв’язання. Спочатку селянин переправляє козу, потім повертається й перевозить на другий берег капусту. Залишивши на цьому березі капус­ту, він везе козу назад. Наступним рейсом селянин перевозить вовка. І нарешті їде по козу. Можливе й інше розв'язання.

Задача 3. До річки під'їхали чотири лицарі зі зброє­носцями й знайшли один тримісний човен. Чи можуть вони переправитися на другий берег за умови, що, опинившись окремо від свого лицаря, жоден зброєносець не перебу­вав би при цьому в товаристві інших лица­рів? Лицарі теж погодилися гребти.

Розв’язання. Позначимо лицарів буквами А, Б, В, Г, а їх зброєносців — відповідно а, б, в, г. Спочат­ку переправляються на другий берег зброє­носці б, в, г. Зброєносець б повертається, а лицарі В і Г переправляються на другий бік. Лицар В і його зброєносець повертають­ся назад. Потім лицарі А, Б, В, переправ­ляються на другий берег. Зброєносець г за­бирає зброєносців б і 6. Один зі зброєносців перевозить останнього зброєносця а.

Задачі на рух

Задачам на рух відведено значну роль серед усіх задач, які розв'язують у школі.

Труднощі, що виникають під час їх розв'я­зування, пов'язані з багатьма обставинами, зо­крема з великою різноманітністю типів задач: на зустрічний рух, на рух у протилежних напрям­ках з одного пункту, в одному напрямку з одно­го або різних пунктів, причому, як за одночасно­го, так і за неодночасного початку руху, на рух за течією й проти течії, а також на рух одного предмета щодо іншого. Одне із завдань навчання математики — сформувати вміння вивчати рух.

Задачі на рух можна розподілити на такі види:

• Задачі на односторонній рух.

• Задачі на рух в різних напрямах.

• Задачі на зустрічний рух.

• Задачі на рух за течією та проти течії.

Одним із способів розв'язування текстових задач є арифметичний, що спрямований на розвиток мислення. Доцільно ще раз повторити, яка залежність є між даними величинами: відстанню, часом та швидкістю:

Швидкість показує, яку відстань проходить об'єкт за одиницю часу; наприклад, скільки кілометрів за одну го­дину проїжджає автомобіль; скільки метрів за одну хви­лину пропливає плавець; скільки метрів за одну секунду пробігає спортсмен.

Для перевірки уміння розв'язувати задачі можна запропонувати завдання такого плану:

1. Автомобіль проїхав 120 км за 3 години. З якою швидкістю їхав автомобіль?

2. Автомобіль їде із швидкістю 60 км/год. Яку відстань проїде він за 4 год?

3. Автомобіль їде із швидкістю 50 км/год. За який час він проїде 100 км?

4. Заповніть таблицю, де S - це шлях, t – час руху, V - швидкість руху, і запиши формули залежності величин:

Текст задачі і розв'язання записуємо в зошит, і вико­ристовуємо як опорний конспект у разі виникнення труд­нощів.

При розв'язуванні задач на зустрічний рух і рух у про­тилежних напрямах знайомимо учнів з термінами «швидкість віддалення» та «швидкість зближення».

Якщо два об'єкти рухаються рівномірно (з постійни­ми швидкостями), то відстань між ними за кожну оди­ницю часу або зменшується, або збільшується на одна­кову кількість одиниць.

Відстань, на яку зближуються об'єкти за одиницю часу, називається швидкістю зближення.

Відстань, на яку віддаляються об'єкти за одиницю часу, називається швидкістю віддалення.

Рух у протилежному напрямі

           Рух з відставанням

           Рух  навздогін

Зустрічний рух

Важливо впевнитись, що учні розуміють усі поняття та терміни, а також ситуацію, описану в задачі. Досить часто цю ситуацію корисно навіть розіграти, доцільним є використання схематичних малюнків, моделей, що доз­воляють представити наочно умову задачі. Учні по­винні набути навичок зображати умову задачі у вигляді схематичного малюнка. Це допоможе їм зрозуміти та за­пам'ятати умову, побачити спосіб розв'язання задачі і перевірити правильність її розв'язання.

Одночасний рух:

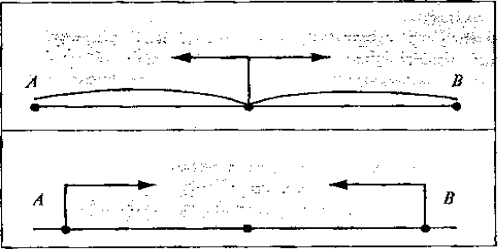
За малюнком одночасного руху можна визначити:

1) з яких точок почався рух;

2) в якому напрямку і з якою швидкістю він відбувався;

3) як змінилась відстань між об'єктами, що рухають­ся, зменшувалась чи збільшувалась, і на скільки;

4) на якій відстані один від одного перебували об'єк­ти в заданий момент часу;

5) де і коли відбулася зустріч, якщо вона відбулася.

Розв'язання текстових задач арифметичним спосо­бом сприяє розвитку мовлення: переказуючи умову, аналізуючи, переформульовуючи її, ставлячи запитан­ня та даючи на них розгорнуту відповідь.

Корисним є детальне розв'язання задачі із повним записом у зошиті, який можна використовувати як зра­зок.

Розрахункові задачі на відсотки

Створення ринкової економіки, утворення спільних підприємств, ВАТ, від­криття банків і фірм, випуск акцій і цінних паперів, розвиток орендних відносин став на сьогодні одним із важливих досягнень люд­ства. Ринкова система постійно розширюється та вдосконалюється. Важливу роль у ринкових відносинах відіграють комерційні банки, які виконують дві основні функції: зберігають гро­шові вклади і надають кредити. Тож сьогодні майбутнє дітей дуже складно уявити без якісної математично-економічної освіти. Життя постійно вимагатиме від них уміння бути діловою людиною. На цьому занятті гуртка вчитимемося складати та розв'язувати задачі на відсотки бізнесово-фінансового характеру, виконуватимемо та перевірятимемо розрахунки банківських від­сотків (простих і складних).

Серед задач прикладного змісту необхідно виділити задачі на відсотки. їх можна розділити на дві основні групи. Перша група — знаходження відсотків від числа, друга група-знаходження числа за його відсотками. За­дачі на відсотки дуже різноманітні, поняття відсотка використовується в різних галузях науки і практики: спла­ви і суміші, кулінарні рецепти, економічні та банківські розрахунки, і т.д. Розв'язання задач можна здійснювати арифметичним, алгебраїчним і геометричним методом, за допомогою пропорції. Відсотки також використову­ють при вивченні діаграм.

Наприклад: річний відсоток по банківському внеску становить 8%. Скільки це буде становити в гривнях, якщо вкласти в банк 35 тисяч гривень?

Розв'язання

Нехай х—шукане число, тоді

35000_____100%

х_________ 8%

= , =

Відповідь: 2800 гривень.

Учням варто запропонувати опорні конспекти для розв'язування задач на відсотки.

• P% від A → А∙ ;
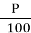• В-це Р% , тоді 100% → В ː ;
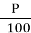• А збільшити на Р% → А+ А∙ );
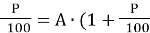• А зменшити на Р% → А- А∙ 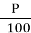= А (1-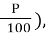

де А, В — деякі величини.

Варто учням запропонувати задачі такого плану, щоб показати «підступність» відсотків.

Наприклад: Ціну товару збільшили на 30%,а через деякий час зменшили на 30%. Порівняти початкову і нову ціну товара, якщо він коштував 80 грн.

Відповідь: початкова ціна більша за нову.

Але як правило, не розв’язуючи задачу, учні роблять висновок, що ціни однакові.

Задачі на розчини і сплави

Розв'язування задач на розчини і сплави по­в'язане з поняттями «концентрація», «відсотко­вий уміст» і базується на таких положеннях:

1) усі суміші (сплави, розчини) однорідні;

2) якщо суміш (сплав, розчин) маси т склада­ється з речовин А, В, С, які мають відповідно маси т₁, т₂, т₃, то величини ,, називаються концентраціями відповідно речовин А, В, С у суміші;

3) величина 100% (100%, 100%) називається відсотковим умістом речовини А (В, С) у суміші;

4) кількість речовин, узятих до змішування, дорівнює кількості речовин, отриманих піс­ля змішування (наприклад, якщо до розчи­ну, у якому міститься т г солі, долили води, то в отриманому розчині буде т г солі; якщо змішати два розчини, один із яких містить т г солі, а другий — п г солі, то в отрима­ному розчині дістанемо (т + п) г солі).

ПОВТОРЕННЯ ОСНОВНИХ ТИПІВ ЗАДАЧ НА ВІДСОТКОВІ РОЗРАХУНКИ

Розв’язування задач

Задача

Скільки грамів 10%-го і 15%-го розчинів солі необхідно взяти, щоб одержати 40 г 12%-го розчину?

Розв'язання. Нехай для утворення суміші необхідно взяти х г 10%-го розчину. Система­тизуємо дані задачі у вигляді таблиці:

За умовою задачі складаємо рівняння:

         0,l х+0,15(40- х) = 0,12∙40, 0,1 х+6-0,15х = 4,8,

                     0,05х = 1,2, х = 24.

Отже, треба взяти 24 г 10 %-го розчину і 40-24 = 16г 15%-го розчину.

Відповідь. 24 г і 16 г.

«Лавинні задачі»

Іноді зустрічаються обчислення, які ми, не замислюючись, відразу починаємо виконувати в зазначеному порядку, якими б громіздкими вони не виявилися. Тим часом нерідко буває, що досить змінити порядок дій, винести який-небудь множник за дужки або зробити інші по­дібні найпростіші перетворення, що спираються на основні закони арифметики, — і обчислення значно спроститься.

Назвемо «лавинними» задачі, під час розв'я­зування яких після застосування ефективного й ефектного прийому починається процес скоро­чення або спрощення, завдяки чому розв'язання стає легким, простим.

На цьому занятті розв’жемо такі задачі:

Задача 1. Відомий німецький математик Га­усс дуже рано виявив блискучі здібності до ма­тематики. Розповідають, що одного разу його шкільний учитель запропонував учням знайти суму всіх чисел від 1 до 100 включно. Тільки вчитель прочитав завдання, як маленький Гаусс сказав: «Готово! 5050». Як він міг швидко об­числити цю суму?

Розв'язання. Гаусс помітив, що пари чисел, які віддалені від кінців ряду 1, 2, 3, ...,98, 99, 100: 1 і 100, 2 і 99, 3 і 98 і таке інше, склада­ють у сумі 101. Тобто:

1 + 2 + 3+4+5+6 + ... + 95 + 96 + 97 + 98 + 99+100 = (1 + 100)+(2 + 99) + (3 + +98) + (4 + 97) + (5+96)+...+(50 + 51).

Оскільки таких пар 50, то потрібно 101 по­множити на 50, дістанемо 5050.

Задача 2. Знайдіть простий спосіб й скорис­тайтеся ним для обчислення суми: + + + …+  .

Розв'язання. Оскільки = 1-, = - і т. ін., то + + + …+  = (1-)+( - )+…+( - ) = 1- = .

Задача 3. Обчисліть усно:

.

Розв'язання. Обчислення прикладу спростить­ся, якщо зауважити, що

                             10² +11² +12² = 13² +14² =365.

Тоді

= + = 1+1=2.

Задачі судоку

Останнім часом у світі набула поширення японська гра судоку, яка зводиться до такого: дається квадрат 9x9, у деяких клітинах якого написано цифри від 1 до 9; пропонується всі по­рожні клітини заповнити цифрами так, щоб у кожному рядку, кожному стовпці і в кожному з дев'яти виділених квадратів усі цифри були різні. Ця гра подобається багатьом дорослим, тому завдання судоку часто друкується в газетах і журналах. Дітям вона подобається ще більше. А гра ця суто математична: судоку — це цікава математична задача. Тому було б непогано, коли б і школярі ознайомилися з нею. Крім усього ін­шого, гра судоку розвиває в учнів своєрідну «просторову уяву»: учень вчиться бачити всю таблицю, окремо — її рядки, стовпці і виокрем­лювати квадрати 3x3. Цим вона схожа на шахи, але набагато простіша й зрозуміліша.

Вправи судоку бувають різних рівнів склад­ності. Є досить прості, доступні навіть учням по­чаткових класів, є важчі — для старшокласни­ків і студентів. Залишаються ще й нерозв'язані проблеми — непогані теми для дослідження нау­ковців. У навчанні математики гру судоку мож­на використовувати по-різному. Наведу вправу, пристосовану для занять гуртка.

Задача. Яку цифру слід поставити в центральній клітині судоку на рисунку 1?

                       Рис. 1

Розв'язання. У четвертому й шостому стовп­цях є одна й та сама цифра 6. Тому в централь­ному квадраті ця цифра не може бути ні в ліво­му, ні в правому стовпці. Отже, вона може бути в середньому стовпці.

Відповідь. Цифра 6.

На сьогодні опрацьованої теорії судо­ку поки що не існує. Є спроби застосувати до розв'язування судоку многочлени спеціальних видів, різнокольорові графи тощо. Але всі вони малоефективні і потребують часу в кілька разів більше, ніж звичайно. Усе ж для дослідників-початківців тут багато цікавих проблем.

Як створювати судоку? Якщо накреслити квадрат 9x9 і в деяких клітинах написати до­вільно цифри від 1 до 9, то найімовірніше, що в такому разі судоку не матиме розв'язку. Най­цікавіші судоку, які мають один розв'язок. Скільки розв'язків може мати судоку? Як і реш­та математичних задач, головоломка судоку може бути визначеною, якщо має єдиний розв'язок, або невизначеною, якщо має кілька розв'язків. Трапляються і некоректно складені судоку, які не мають жодного розв'язку.

Що таке розв'язок судоку? Якщо в завданні не вказується, які клітини слід заповнювати, то мається на увазі, що заповнити треба всі порожні клітини. У цьому випадку розв'язок судоку — це правильно заповнена цифрами вся таблиця. Тоб­то заповнена так, що в кожному її рядку, кожно­му стовпці і в кожному виділеному квадраті всі цифри різні.

Трапляється, що задача має два чи більше різних розв'язки.

Звичайно, судоку — гра для одного. Але її можна пристосувати для змагання кількох. На­приклад, копії одного й того самого судоку розда­ти учасникам гри і провести змагання: хто запо­внить швидше. Можна на всьому полі судоку виді­лити рівні за площею частини для кожного гравця і змагатися: хто перший правильно заповнить свою частину. Можливі й інші варіанти. А взагалі гра судоку заслуговує на те, щоб із нею ознайоми­ти учнів. Найкраще це зробити на уроках матема­тики або на заняттях математичного гуртка.

Видатні математики

ЧОМУ ПОТРІБНО ВИВЧАТИ БІОГРАФІЇ ВИДАТНИХ МАТЕМАТИКІВ?

Чинна програма з математики зазначає про необхідність широко використовувати у ви­вченні предмета відомостей з історії науки, ознайомлювати з боротьбою ідей, долею матема­тичних відкриттів та їх авторів тощо. Головна мета використання на уроках історичного ма­теріалу та біографій видатних математиків — сприяти зацікавленості предметом, підвищити загальну культуру, розширити світогляд, ак­тивізувати пізнавальну діяльність учнів. За­вдяки історичному матеріалу учні формують уявлення про математику як невід'ємну час­тину загальнолюдської культури, залучаються до наукової творчості, краще розуміють сучас­ний стан науки. Розуміння історії математи­ки, внеску вітчизняних учених у її розвиток є одним із головних аспектів гуманітаризованого світогляду як основи загальноосвітнього стандарту з математики. Формування позитивних рис характеру особистості нале­жить до завдань освітньої галузі «Математи­ка» у середній школі, виконанню яких сприяє також ознайомлення з історико-біографічним матеріалом. Уведення у викладання людсько­го фактору дозволяє подавати учням науку, не лише згадуючи прізвища її творців, а й озна­йомлюючи з життям конкретних особистостей, досягнення яких можна брати за зразок. У по­шуках життєвого вибору дитині дуже важливо мати взірець для наслідування; не виключено, що таким може стати хтось із видатних мате­матиків.

Ознайомлення з біографіями творців мате­матики дозволяє по-справжньому полюбити цю науку. За словами. М. І. Кованцова, «любов до математики стане ще більшою, коли побачиш не тільки саму науку, а й тих численних по­движників, які, не шкодуючи зусиль, цілком віддали себе великій справі служіння мате­матиці і, неначе яскраві факели, освітлювали в ній шлях далеко вперед». Вивчення життя і творчості видатних математиків спри­яє вихованню почуття патріотизму, культури поведінки, «узагальнює культуру мислення, дисциплінує її, виховує об'єктивність, інтелек­туальну чесність, і таким чином сприяє форму­ванню наукового світогляду ».

Значно більше можливостей ознайомити з біографіями творців науки вчитель має в позакласній роботі з математики.

Підсумкове заняття

Математика — це не тільки формули, зако­ни і графіки, але й люди, їхнє життя, почуття, доля. Кожен період історії математики багатий на видатних учених. Одні зажили слави і без­смертя ще за життя, іншим судилося пройти складний шлях і розділити трагічну долю сво­го народу. Багато визначних математиків стали зразками патріотизму й щирої відданості науці.

Усупереч складній історичній долі, числен­ним поневолювачам, наша Україна все ж дала світові геніальних сподвижників слова, куль­тури, освіти, науки й технологій. Нині є акту­альним завдання правдиво відтворити історію розвитку науки й культури в Україні, не забути жодного імені серед учених, творіння якого по­служать гідним зразком для нащадків, викли­чуть гордість українців як етносу, який долучив до світового прогресу.

Доробок генія належить цілому світові. І це правильно. Але серце кожного належить своїй і тільки своїй Вітчизні.

Щедра талантами українська земля подару­вала людству не тільки чудових співаків, ком­позиторів, письменників, а й визначних математиків.

Підсумкове заняття математичного гуртка доцільно провести за таким планом:

1. Вступ.

2. Остроградський Михайло Васильович.

3. Геній з українським серцем.

4. Світ не знав лише, що він українець.

Література:

1.Депман І.Я. Історія арифметики: посібник для вчителів. - М.: Просвітництво, 1965.

2. Олехнік С.Н., Нестеренко Ю. В., Потапов М. К. Старовинні цікаві завдання. - М.: Наука. Головна редакція фізико-математичної літератури, 1988.

3. Перельман Я. І. Цікава алгебра. Цікава геометрія. - М.: ACT, 2006.

4. Бабінська І. Л. Завдання математичних олімпіад. - М.: Наука, 1975.

5. Пічурін Л. Ф. За сторінками підручника алгебри. - М.: Просвітництво, 1990.

6. Глейзер Г. І. Історія математики у школі. VII-VIII кл.: Посібник для вчителів. - М.: Просвітництво, 1982.

7. Мантуров О. В. та ін. Математика в поняттях, визначеннях та термінах. -М.: Просвітництво, 1978.

8. Бевз Г. П. Математика: 6 кл.: підр. для загальноосвіт. навч. закл. - К.: Генеза, 2006.

9. Депман І. Я., Віленкін Н. Я. За сторінками підручника математики: посібник для учнів 5-6 кл. середовищ. шк. - М.: Просвітництво, 1989.

10. Пічурін Л. Ф. За сторінками підручника алгебри: кн. для учнів 7-9 кл. середовищ. шк. - М.: Просвітництво, 1990.

11. Енциклопедія для дітей. Т. 11. Математика/глав, ред. М. Д. Аксьонова. - М: Аванта +, 2002.

12. Литвиненко Г. Н., Мордкович А Г. Практикум з елементарної математики. - М.: Просвітництво, 1991.

13. www.encspb. ru

14. www.bank. gov. ua

15. studprofkom. ntu-kpi.kiev.ua

16. www. peoples, ru/science

17. http://dic.academic.ru

18. www.zn.ua

19. http://son.org.ua

20. Романець Д. Діаграми Вороного // Україна мо­лода. — 2008.

21. Боднарук Л. Український геній математики // Шлях перемоги. — 2004.

22. http://uk.wikipedia.org

23. Шокало О. Видатні українці // ІМІДЖ UA. — 2009. — № 1(6). — С. 105