Бінарний урок. " Дроби та ноти "

                                                 Бінарний урок

з  математики  та  музичного  мистецтва

Тема: «Дроби та ноти»

                         «Математика й музика   потребують     єдиного  мислення»

                                                                                                 (А. Енштейн)

Мета уроку:   

Навчальна:     

повторити  теоретичні знання про історію виникнення дробів, їх позначення, означення чисельника, знаменника та звичайних дробів;

узагальнити отриманні знання про дроби на застосуванні їх в музиці, продовжуючи знайомство з нотами та їх довготою;

систематизувати практичні навички додавання та віднімання дробів з однаковими знаменниками, обчислюючи музичний такт дитячих народних пісень;

     Розвивавати логічне  мислення,   правильне  наукове  мовлення,  увагу,  пам'ять, зосередженість, уважність,  розумові здібності;

Виховувати стійкий інтерес  до шкільних  предметів,  розкриваючи зв`язок між ними; розширити словниковий запас  учнів та  компетентність про музичні твори та  математичні дроби.

Тип уроку: узагальнення та систематизація знань та вмінь.

Обладнання:

ІКТ , комп. презентація, картки для учнів,                                                   опорна схема «Дроби та ноти».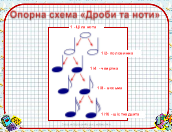                                                                                               

  Хід урока:

I    Організаційний  момент. (слайд 1)

Вчитель математики: Математика та музичне  мистецтво – два шкільних предмета, два полюса людської культури. Слухаючи музику, ми переносимося у магічний світ звуків. Розв`язуючи задачі, ми поринаємо у логічний та точний світ чисел. Ми не задумуємося над тим, що світ звуків та простір чисел із давних давен  знаходяться поруч  один з одним. А тому:  «Математика й музика  потребують     єдиного  мислення». Ці  слова  Енштейна стануть епіграфом сьогоднішнього уроку.

(Слайд 2)

    Древньогрецький філософ, математик, музикант ПІФАГОР першим  побачив  та об`єднав  ноти з дробами. Він вивчав   математичну сторону звука,  шукав зв`язок між астрономією   та музикою.

Вчитель музики:   Ми живемо у світі звуків. Люди дуже давно навчились записувати різні звуки за допомогою спеціальних знаків. Колись, перебираючи струни на арфі, учений Піфагор помітив, що наймилозвучніше співвідношення звуків – це октава -1/8, квінта – 1/5 і кварта –  1/4. Піфагор уперше математично описав звук. Тому його цілком можна називати «прадідом» акустики. Його октава стала виражатися так: (слайд 3)

 1          1/2       1/3          1/4          1/5       1/6        1/8         1/16

до ре мі фа соль        ля    сі     до

Вчитель математики:  Ви  вже зрозуміли, що на сьогоднішньому уроці ми узагальнимо знання про звичайні дроби ,а   також закріпимо навички порівняння та  додавання і  віднімання з ними. 

Вчитель  музики (звертається до математика) Але ж цей урок незвичайний – в ньому поєднані разом музичне  мистецтво  з математикою. Тому учні повторять  також види нот, їх звучання, прослухають мелодії та заспівають пісні.

Вчитель математики:  А що ж спільного між цими двома завданнями? Чи не підкажете тему сьогоднішнього уроку?  («Дроби та ноти»)  ( слайд 4).Так,  і тому за кожне правильно  виконане  музично-математично   завдання кожний із вас отримуватиме  медальку. Чим більше медальок  назбирає  команда – та  і команда буде переможцем, яка в нагороду отримає солодкий  подарунок. А оцінювати  правильність  відповідей та  швидкість  їх  виконання  нашими командами – буде  наше шановне  жюрі. 

II.     Із історії музики та нот

Вчитель  музики  Музика немислима без нот, кожна з яких має свою тривалість. (слайд 5-6-7-8-9-10)

Вчитель  музики: А тепер завдання  командам, хто швидше  піднявши руку  поставить  дріб у відповідність  до кожної ноти,  який відповідає  її тривалості?

( робота на дошці з карточками)

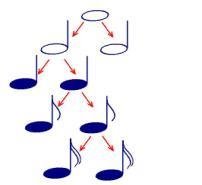
 III.  Вчитель математики:   Нотна     математика  (слайд 11)

Опорна схема «Дроби та ноти»

 

 

 

 

 

 

 

Висновок ( вчитель математики): А  тепер давайте  подивимось на зв’язок  нашої  теми із  музичним  мистецтвом.

IV      Індивідуальна   робота .

•     Порівняємо тривалість  звучання нот.  (Включається слайд  12) 

Вчитель  математики: А  тепер  подивимось  та  порівняємо  з  точки  зору  математики  та поставимо знаки:

   

 

 

 

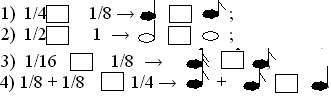
(слайд 13)

V. Вчитель  математики: Пропоную командам  завдання з карточками на  швидкість , а наше  жюрі буде спостерігати  за  правильністю  його  виконання;

Вчитель музики:  А  що  таке  розмір в  музиці ?  ( слайд  14) .Які ви знаєте розміри ?

 

VI. Групова дидактична гра «Відгадайка»  (слайд  15-16)

Вчитель музики: Погляньте на нотний стан, що на слайді. Він розбитий вертикальними рисками на частинки , що називаються  тактом. Довести відповідність тривалості в такті. Для цього порахуйте загальну тривалість нот у кожному такті, запишіть у зошитах усі розрахунки у вигляді дробів із знаменником «4»

 

Перевіримо, порівнюючи із слайдом

1-ий такт    1/4 + 1/8 + 1/8 + 1/4 = 3/4;

2-ий такт    1/4 + 1/8 + 1/8 + 1/4  = 3/4;

3-ій такт     1/4 + 1/8 + 1/8 + 1/4  = 3/4; 

4-ий такт    1/4 + 1/8 + 1/8 + 1/4 = 3/4;

5-ий такт    1/4 + 1/8 + 1/8 + 1/4 = 3/4.

6-ий такт    1/4 + 1/8 + 1/8 + 1/4 = 3/4.

 

Як бачимо загальна тривалість кожного такта 3/4. Це число називається розміром  музичного  твору. Записується розмір твору завжди на початку нотного стану.

VI.   Музична фізхвилинка   (слайд 17)

 

Вчитель музики  : пропоную вам переглянути  відео  та прослухати , який з  жанрів  музики  звучить і визначити  його  розмір – команда, яка  впорається із цим завданням  отримає медальки: полька, вальс, марш учні визначають що де ?

(перегляд  відео)

VII.       Вчитель  математики : Робота  з  підручником № 788 ( слайд 18)

 

VIII.     Дидактична гра « Музично-математична   рибалка» (слайд 19)

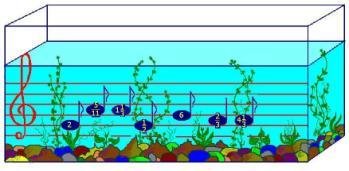На початку уроку  учні були розбиті на групи однакові  за рівнем навчання .

  

IX.   Тест-узагальнення «Дроби та ноти» (слайд  20)

              Вчитель математики:

• Які вирази про дроби правильні?

а)Знаменники усіх дробів парні числа.

б) Дроби відповідають у музиці тривалості  нот.

в) Розмір музичного твору записується дробовим числом.

• Назвіть   дріб , що  відповідає  цій   ноті:

 а )  ¼     б) ½     в) 1/8

• Який із дробів найменший: 1/4; 1/16; 1/2:; 1/8.

 а )  1/16     б)    ½     в) 1/8

• У якому порядку розміщенні дроби: 1/16; 1/8; 1/4; 1/2.

         а) зростання б) спадання

X.   Підсумок уроку.

      Вчитель музики: Як багато  в музиці  математики — і розміри, і тривалість нот… Та це ще не все, бо існує в музиці і «музичне множення», «музичне додавання».

Вчитель математики:  Якщо з науки математики вирізати знання про «Звичайні дроби», то зникне і музика, яку ви так любите, зникнуть і музичні інструменти, ноти. 

Пісня   (слайд 21)

   (під  мелодію пісні  «Вчать  у  школі»)

               1.Дроби легко нам учить,

                 Бо ж без них  нам не прожить ,

                 Друзі ціле число можуть підсказати

                 Одну другу поділить  і  помножити  в  цю  ж мить

                 На  уроці  вправно  можем  рахувати  - 2р.

 

                            2.Це число із двох частин,

                            Риска дробу ніби тин.

                           Те, що зверху, називається чисельник

                           А під рискою завжди, памятай і не блуди,

                           Бо під рискою завжди стоїть знаменник- 2р.                                                                                                                                                          

 

Список використаної літератури:

1.Стадник Л. Г. Математика. 5 клас: Плани-конспекти уроків. — Х.: Веста: с. 76 Видавництво «Ранок», 2005. — 416 с.

 2.Баран О. І. Математичні мініатюри. — К.: Ленвіт, 2007. — 205 с.

 3.Губа Л. А. Нетрадиційні уроки математики. — Х.: Вид. гр. «Основа», 2006.

  4.Корнієнко Т. Л. Тиждень математики в школі / Т. Л. Корнієнко, В. І. Фіготіна. — Х.:    Веста: Видавництво «Ранок», 2008. — 176 с. (Бібліотека творчого вчителя).

   5.Рибчук Г. Математика і музика. Нетрадиційний урок у 6 класі // Математика. — №46 (446). — 2007.

     6. Бабіченко С. В. Порівняння раціональних чисел // Видавн. гр. «Основа» — №3 (123). — 2006 р.