Числові множини- теорія, презентація до уроку
Про матеріал
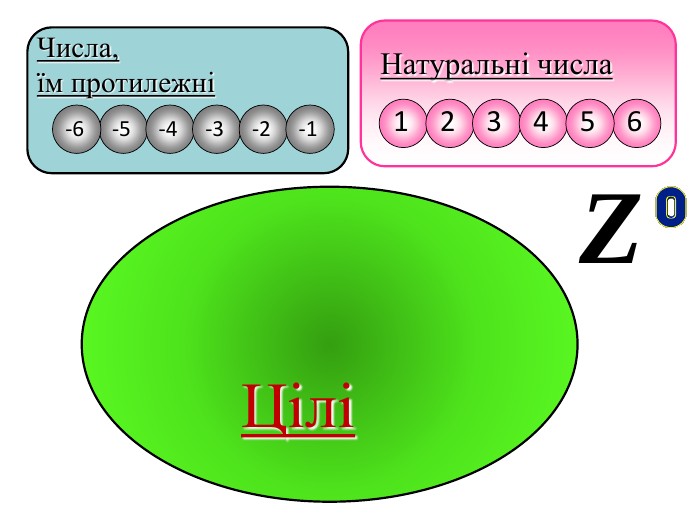
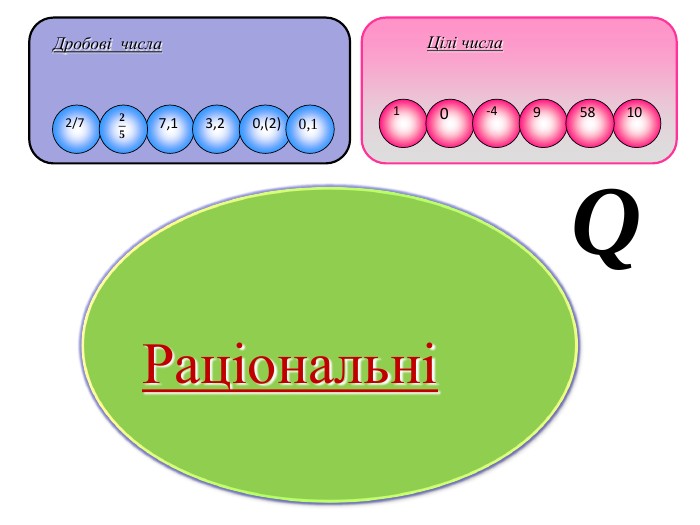
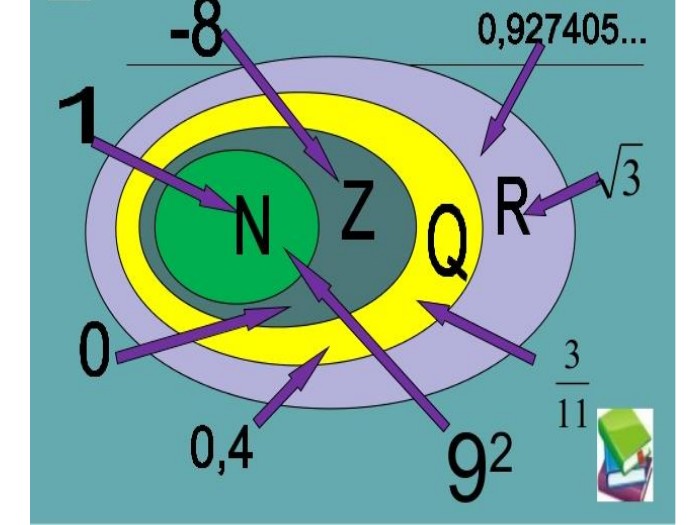
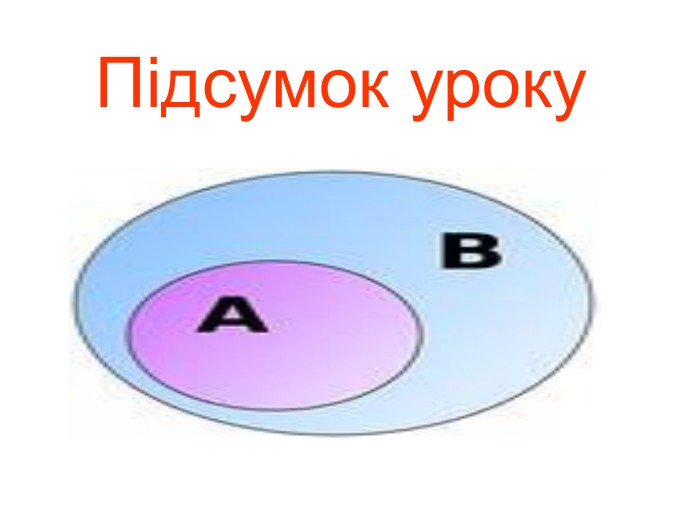
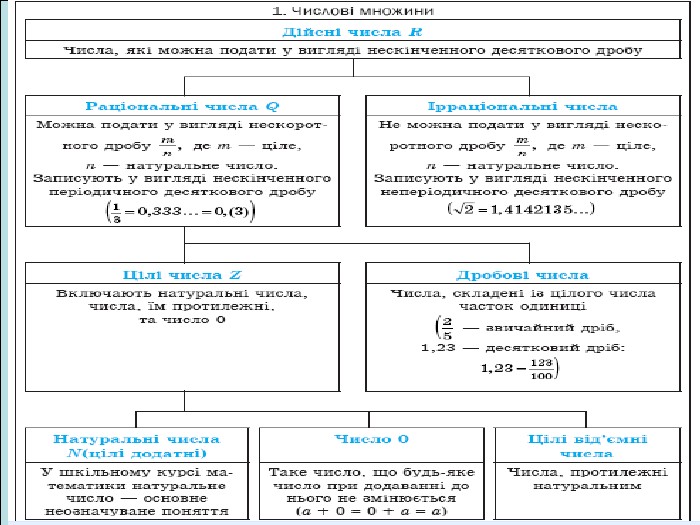
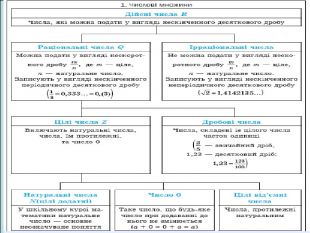
Ця робота містить теоретичний матеріал до уроку на тему «Числові множини», практичний матеріал з розв’язком ( зразком), матеріал для самостійної роботи. Також пропонується презентація з даним матеріалом Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
ppt
До підручника
Алгебра 8 клас (Мерзляк А. Г., Полонський В. Б., Якір М. С)
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку



































-

Koval Babak
16.02.2025 в 20:33
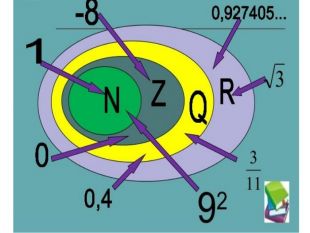
У презентації є помилка у використанні Символу Справжньої Підмножини ⊂
Має бути: N⊂Z⊂Q⊂R⊂C
C - це комплексні числа.
детальніше і пояснення тут:
https://naurok.com.ua/mnozhini-operaci-nad-mnozhinami-282191.html
Загалом дякую за презентацію!
Загальна:
4.3
Структурованість
3.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Кобижский Анатолій
29.01.2025 в 03:13
Загальна:
4.7
Структурованість
4.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Мирошниченко Зоя Михайлівна
22.01.2025 в 08:59
дякую
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Новомлинська Дар'я Сергіївна
05.03.2024 в 21:08
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Вигоднер Діана Ісаківна
14.02.2024 в 01:51
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Кухтін Юлія Олександрівна
15.01.2023 в 12:18
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Грунська Наталя Миколаївна
17.12.2022 в 07:42
Загальна:
4.0
Структурованість
4.0
Оригінальність викладу
4.0
Відповідність темі
4.0
Показати ще 4 відгука