Числовий промінь. Шкала. Види шкал, їх використання. Самостійна робота

УРОК № 9

Тема. Числовий промінь. Шкала. Види шкал, їх використання. Самостійна робота

Мета: сформувати в учнів поняття про шкали і координатний промінь як окремий випадок нескінченної шкали; роз'яснити зміст і навчити зна­ходити ціну поділки шкали, для того, щоб знаходити число, що відповідає певній точці шкали.

Тип уроку: засвоєння нових знань.

Обладнання: різні вимірювальні прилади, що мають шкали (термо­метр, динамометр, вольтметр, годинник, ваги), паперові моделі шкал з різними показниками.

Хід уроку

I. Перевірка домашнього завдання

 Перевірку засвоєння матеріалу попереднього уроку слід провести у вигля­ді невеличкої самостійної роботи (перевірити її тільки в учнів, що мають деякі проблеми із засвоєнням математичних понять), усі інші учні перевіря­ють правильність виконання самостійно, звіряючись із роботою, яку вико­нав учень за дошкою, або ж із записами, зробленими за дошкою вчителем.

Самостійна робота.

1. Яким числам відповідають точки А, В, С, D, Е (рис. 13)?

2. Накресліть координатний промінь і позначте на ньому точки, що відповідають числам 0; 1; 3; 7; 8.
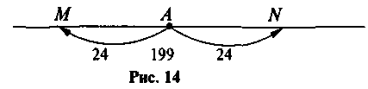
3. Знайдіть координати точок М і N, що знаходяться на кінцях стрілочок (рис. 14).

II. Актуалізація опорних знань

Запитання до класу

1. Чи має координатний промінь початок? кінець?
2. Як називаються числа, що відповідають точкам координатного променя?
3. Відомо, що М(т) лежить праворуч від точки N(п), але ліворуч від точ­ки K(k). Що можна сказати про числа m i n; m i k; n i k?

ІІІ. Доповнення знань

(Евристична бесіда) Ми знаємо, що для позначення натуральних чи­сел застосовують координатний промінь. Як позначити на цьому промені точку, що зображує натуральне число пі (Вибрати одиничний відрізок і відкласти його и разів від початку променя.) А чи не можна застосувати координатний промінь для інших цілей? (в інших випадках?) Давайте по­дивимось на ці вимірювальні прилади. (Вчитель показує демонстраційні моделі приборів зі шкалами.) Чи не є частина координатного променя скла­довою частиною всіх цих приладів?

Після цього вчитель пояснює, що всі частини приладів мають назву «шкала» і схожі за будовою (показувати «будову» шкали, пояснювати по­няття «штрих», «ціна поділки», краще починати із знайомих приладів: де­монстраційної лінійки, годинника, демонстраційного амперметра тощо.)

Після цього вчитель пояснює, що координатний промінь є особли­вим випадком — нескінченною шкалою з ціною поділки — 1 одиничний відрізок. У загальному ж випадку, щоб визначити, якому числу відповідає точка шкали приладу, треба знайти ціну поділки (одиничний відрізок), а потім, як і у випадку з координатним променем, знайти відстань від по­чатку шкали в поділках, помноживши на ціну поділки.

IV. Закріплення знань учнів

1. Робота зі шкалами

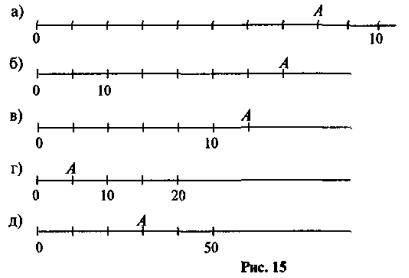
1) Знайдіть ціну поділки й число, яке зображує точка А на кожному із ри­сунків (рис. 15).

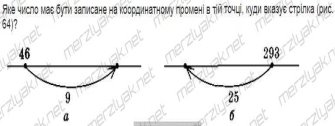
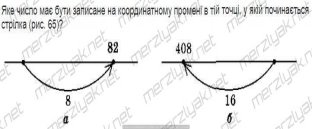
2) № 134.           В(17),  С(11)

№ 135-136

               V. Підсумки уроку

VI. Домашнє завдання

п. 5, № 129,126