Чотирикутники у 8 класі
![]()

вчитель математики
Димчогло Катерина Степанівна
Мета. Систематизувати отримані знання з теми «Чотирикутники»; розвивати вміння розв’язувати задачі, творче мислення; учити цінувати думки та працю інших; розвивати математичну мову, інтерес до математики.
Очікувані результати.
У процесі уроку учні зможуть:
– повторити вже вевчений матеріал з теми;
– удосконалити свої вміння та навички розв’язувати задачі з вивченої теми;
– поглибити свої знання історичним матеріалом;
– виховувати інтерес до математики.
Обладнання. Моделі планіметричних фігур, таблиця, «заморочки з бочки», конверти з задачами, тестові задачі, мультимедійна дошка, турнірна таблиця.
Підготовка до заняття.
1) Учні класу об’єднуються в чотири команди. Кожна команда обирає собі:
а) назву; б) капітана; в) костюми(або емблеми), а також готує спосіб відрекомендувати команду, обгрунтувати її назву.
2) Парти слід розставити так, щоб кожна команда сиділа за «круглим столом».
Хід уроку.
1. Організаційна частина.
1.1 Привітання з класом.
1.2 Повідомлення теми, мети, очікуваних результатів уроку та правил гри.
1.3 Вступне слово вчителя.
2. Проведення уроку-гри.
Урок розпочнемо епіграфом:
«Математика цікава тоді, коли
дає поживу нашій винахідливості
й здатності до міркувань»
П. Пойа
Записуємо в зошити тему уроку. Щоб досягти мети нашого уроку, проведемо його у формі гри. Об’єднаємо учнів класу в чотири команди, виберемо капітанів та назву команди. Змагання між командами буде складатись з семи геймів.
На мультимедійній дошці висвітлюється
І гейм «Хто більше?».
Командам ставиться по 5 запитань. За кожну правильну відповідь – 1 бал.
На дошці висвітлюється запитання для команди «Паралелограм».
1. Яку фігуру називають чотирикутником?
2. Сформулювати означення паралелограма та його властивості.
3. Як формулюється теорема про середню лінію трикутника?
4. Які види чотирикутників ви вивчали? Знайти серед запропонованих моделей фігур.
(моделі планіметричних фігур розміщені на стенді)
5. Сформулювати властивості квадрата.
На мультимедійній дошці висвітлюється запитання для команди «Прямокутник».
1. Як називають відрізок, який сполучає протилежні вершини чотирикутника?
2. Сформулювати означення та властивість прямокутника.
3. Як формулюються ознаки паралелограма?
4. Сформулювати означення трапеції та властивість рівнобедреної трапеції.
5. Сформулювати теорему про властивість середньої лінії трапеції.
На мультимедійній дошці висвітлюється запитання для команди «Ромб».
1. Які сторони чотирикутника називаються сусідніми? Протилежними?.
2. Сформулювати означення та властивості ромба.
3. Що називається середньою лінією трапеції?
4. Серед запропонованих моделей фігур знайти рівнобедрену трапецію і прямокутну трапецію.
5. Сформулювати ознаку прямокутника.
Виставляємо бали в турнірну таблицю за І гейм.
На мультимедійній дошці висвітлюється
ІІ гейм «Гості з країни «Чотирикутники»
Гостями нашого уроку є казкові герої Паралеограм, Прямокутник, Ромб.
Потім висвітлюється задача казкового героя Паралелограма для команди «Паралелограм».
Знайдіть серед даних чотирикутників мене. Чому ви так вважаєте?
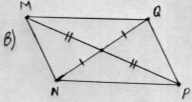
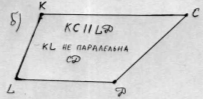
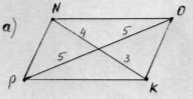
Задача казкового героя Прямокутника для команди «Прямокутник».
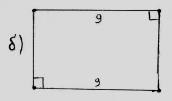
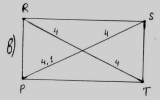
Я і мої брати-прямокутники вирішили відпочити, та серед нас затаїлися нікчеми чотирикутники. Знайдіть їх. Відповідь поясніть.
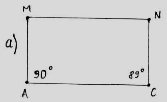
Задача казкового героя Ромба для команди «Ромб».
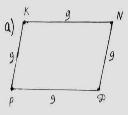
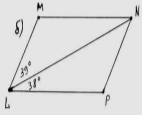
Відшукайте злих паралелограмів, які поневолили моїх друзів Ромбів. Поясніть свої дії.
За правильні відповіді команди отримують по 1 балу і результати записуємо в турнірну таблицю.
Після цього вивішую на дошку таблицю з властивостями вивчених фігур (паралелограма, прямокутника, ромба, квадрата). Учням роздаю такі самі маленькі таблички. Колективно заповнюємо їх. Ці таблички будуть підсумком теоретичного матеріалу.
На дошці висвітлюється
ІІІ гейм «Ви – нам, а ми – вам».
Учням класу було дано завдання підготувати по два запитання історичного характеру для команд-суперників, використавши матеріали підручника «Геометрія. 8 клас», з якого вони навчаються, та історичний матеріал зі стендів, які є в кабінеті математики.
Запитання команди «Паралелограм».
1. Назвати трьох давньогрецьких математиків.
2. Хто такий Фалес Мілетський?
Запитання команди «Прямокутник».
1. Звідки походить слово «Ромб»?
2. Звідки походить слово «Паралелограм»?
Запитання команди «Ромб».
1. Звідки походить слово «Квадрат».
2. Назвати не менше, ніж трьох відомих українських математиків.
За правильні відповіді команди отримують по 1 балу. Результати записуємо в турнірну таблицю.
На мультимедійній дошці висвітлюється
ІV гейм «Умій продовжити…»
На дошці підготовлено рисунок до теореми Фалеса. Учні повинні сформулювати теорему, записати, що дано і що треба довести, а також довести теорему. Капітани призначають по 1 учаснику.
Учень однієї з команд формулює теорему, записує, що дано і що треба довести.
Учень іншої з команд починає доведення. Доводить і навмисно зупиняється.
Учень третьої команди має завершити доведення теореми.
Хто за ким має виходити до дошки вирішать номери, записані на карточках, які потягнуть учні.
За правильно виконане завдання – 1 бал. Один раз кожна команда може надати допомогу своєму товаришеві або замінити його. В другому випадку 1 бал перейде до команди-суперника.
Результати записуємо в турнірну таблицю.
На мультимедійній дошці висвітлюється
«Заморочки з бочки».
Команди по черзі витягують з «бочки» запитання-задачі і зразу дають відповіді. Якщо не може учень відповісти зразу, то учасники його команди допомагають. За кожну правильну відповідь 1 бал.
Задачі.
1. Одна сторона паралелограма дорівнює 6 см, а друга – на 2 см більша. Знайти периметр паралелограма. Відповідь. 28 см.
2. У ромбі один з кутів дорівнює 1350. Знайти інші кути ромба.
Відповідь. 450, 1350, 450.
3. Середня лінія трапеції дорівнює 8 см. Знайти суму її основ. Відповідь. 16 см.
4. Знайти кути рівнобедреної трапеції, якщо один з них дорівнює 700.
Відповідь. 700, 1100, 1100.
5. Шкільна майстерня виготовила партію пластин, що мають форму чотирикутника. Як перевірити, чи пластина має форму прямокутника, маючи лише лінійку з поділками?
Відповідь. Перевірити, чи рівні діагоналі.
6. Учневі доручили виготовити щит, який повинен закрити нішу прямокутної форми. Скільки розмірів і як він повинен зняти, щоб виготовити цей щит?
Відповідь. 2 розміри – довжину і ширину ніші.
Результати V гейму записуємо в турнірну таблицю.
На дошці висвітлюється
VI гейм «Сюрприз із конверта».
На столі лежать три конверти. Капітани команд підходять і вибирають один з конвертів. Читають по черзі умови своїх задач і розв’язують їх біля дошки, а інші учні записують і розв’язують задачу свого капітана в зошитах. На дошці заготовлено рисунок до задач і записано, що дано, що знайти.
За правильно розв’язану задачу 2 бали.
Задачі.
1. Діагональ рівнобедреної трапеції є бісектрисою тупого кута. Знайти бічну сторону трапеції та периметр, якщо її основи дорівнюють 8 см і 12 см.
2. Основи трапеції відносяться як 2:3, а середня лінія дорівнює 25 см. Знайти основи трапеції.
3. Гострий кут прямокутної трапеції дорівнює 600, довжина середньої лінії – 16 см, а більшої бічної сторони 12 см. Знайти довжини основ трапеції. Результати VI гейму записуємо в турнірну таблицю.
На дошці висвітлюється
VІІ гейм «Гонка за лідером».
Учні виконують тестові завдання, заготовлені для кожної команди. Треба серед 4 відповідей вибрати одну правильну. Тривалість виконання тестів – … хв.
За кожне правильно виконане завдання 1 бал.
Відповіді до тестів учні записують у зошити.
Тести для команди «Паралелограм».
1. Якщо периметр паралелограма дорівнює 48 см, а одна з його сторін у 3 рази більша, ніж друга, то більша сторона дорівнює…
А) 6см; Б) 42 см; В) 24 см; Г) 18 см.
Відповідь. Г) 18 см.
2. Діагональ ромба утворює зі стороною кут 650. Чому дорівнює менший кут ромба?
А) 650; Б) 500; В) 1300; Г) 1150.
Відповідь. Б) 500.
3. Послідовно сполучили відрізками середини сторін рівнобедреної трапеції. Назвати вид утвореного чотирикутника.
А) Трапеція; Б) Квадрат; В) Прямокутник; Г) Ромб.
Відповідь. Г) Ромб.
4. Висота рівнобедреної трапеції поділяє більшу основу на відрізки 6 см і 20 см. Знайти середню лінію трапеції.
А) 20 см; Б) 16 см; В) 13 см; Г) 6 см.
Відповідь. А) 20 см.
Тести для команди «Прямокутник».
1. Якщо периметр паралелограма дорівнює 36 см, а одна з його сторін на 4 см більша, ніж друга, то менша сторона паралелограма дорівнює…
А) 5 см; Б) 7 см; В) 11 см; Г) 14 см.
Відповідь. Б) 7 см.
2. Тупий кут ромба дорівнює 1000. Який кут утворює зі стороною ромба його діагональ, проведена за вершини гострого кута?
А) 400; Б) 800; В) 600; Г) 500.
Відповідь. А) 400.
3. Точки А, В, С, D – середини сторін квадрата. Назвати вид утвореного чотирикутника.
А) Квадрат; Б) Ромб; В) Прямокутник; Г) Трапеція.
Відповідь. А) Квадрат.
4. Висота поділяє більшу основу рівнобедреної трапеції на відрізки 4 см і 16 см. Знайти середню лінію трапеції.
А) 26 см; Б) 16 см; В) 20 см; Г) 6 см.
Відповідь. Б) 16 см.
Тести для команди «Ромб».
1. Якщо периметр паралелограма 32 см, а одна з сторін на 2 см менша, ніж друга, то менша сторона дорівнює…
А) 18 см; Б) 7 см; В) 10 см; Г) 3 см.
Відповідь. Б) 7 см.
2. Гострий кут ромба дорівнює 800. Який кут утворює зі стороною ромба діагональ, проведена з вершини тупого кута?
А) 250; Б) 200; В) 400; Г) 500.
Відповідь. Г) 500.
3. Послідовно сполучили відрізками середини сторін прямокутника. Назвати вид утвореного чотирикутника.
А) Ромб; Б) Квадрат;) В) Трапеція; Г) Прямокутник.
Відповідь. А) Ромб.
4. Висота рівнобічної трапеції поділяє більшу основу на відрізки 6 см і 16 см. Знайти середню лінію трапеції.
А) 32 см; Б) 16 см; В) 10 см; Г) 22 см.
Відповідь. Б) 16 см.
Капітани команд кажуть відповіді до своїх завдань. Вчитель записує їх на дошці.
На мультимедійній дошці висвітлюються правильні відповіді до тестів. Порівнявши отримані відповіді з відповідями на дошці, записуємо в турнірну таблицю кількість набраних командами балів.
Визначаємо переможця. Вручення призу. Виставлення оцінок.
Додаткова задача
Фруктовий садок має форму прямокутника, сторони якого відносяться як 16:11, причому його ширина менша за довжину на 250 м. За скільки хвилин охоронець може обійти вздовж огорожі всю ділянку, якщо його швидкість 4 км/год.?
Відповідь. 40,5 хв.
3. Підсумок уроку.
Вертаємось до слайду «Очікувані результати». Робимо висновки.
4. Рефлексія.
Враження учнів класу про урок.
5. Домашнє завдання.
Повторити §§ 19, 22. 7 клас.
1


про публікацію авторської розробки
Додати розробку
