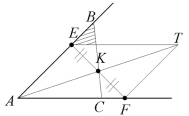
ЧУДОВІ (ВИЗНАЧНІ) ТОЧКИ ТРИКУТНИКА
Відділ освіти Бучанської міської ради
Міський методичний кабінет
Бучанський НВК «СЗОШ І-ІІІ ступенів - ЗОШ І-ІІІ ступенів» № 2
Олександр МУКОЄД
ЧУДОВІ (ВИЗНАЧНІ) ТОЧКИ ТРИКУТНИКА
ЗМІСТ
|
Вступ………………………………………………………………….…………... |
3 |
|
Розділ 1. Точка перетину медіан трикутника…….…………………….…........ |
4 |
|
1.1. Побудова точки перетину медіан (центроїда) трикутника………... |
4 |
|
1.2. Властивості точки перетину медіан (центроїда) трикутника……... |
5 |
|
1.3. Приклади розв’язування задач…………………………………..…... |
9 |
|
Розділ 2. Точка перетину висот трикутника………………………………..….. |
11 |
|
2.1. Побудова точки перетину висот (ортоцентру) трикутника……….. |
12 |
|
2.2. Властивості точки перетину висот (ортоцентру) трикутника….…. |
13 |
|
2.3. Приклади розв’язування задач…………………………………..…... |
19 |
|
Розділ 3. Точка перетину бісектрис трикутника…………………………..…... |
20 |
|
3.1. Побудова точки перетину бісектрис (інцентру) трикутника…..….. |
21 |
|
3.2. Властивості точки перетину бісектрис (інцентру) трикутника….... |
22 |
|
3.3. Приклади розв’язування задач……………………………………..... |
25 |
|
Розділ 4. Точка перетину серединних перпендикулярів до сторін……….….. |
29 |
|
4.1. Побудова точки перетину серединних перпендикулярів до сторін. |
30 |
|
4.2. Властивості точки перетину серединних перпендикулярів……….. |
31 |
|
Розділ 5. Точка перетину симедіан трикутника (точка Лемуана)……………. |
33 |
|
5.1. Властивості точки перетину симедіан трикутника………………… |
34 |
|
Висновок…………………………………………………………………………. |
35 |
|
Список використаних джерел…………………………………………………... |
36 |
ВСТУП
Робота присвячена дослідженню чудових (визначних) точок трикутника.
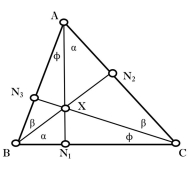
Чудовими (визначними) точками трикутника вважаються точки в площині трикутника, місце розташування яких однозначно визначається трикутником і не залежить від того, в якому порядку беруться сторони і вершини трикутника.
До визначних точок трикутника відносять: точка перетину медіан (центроїд) трикутника, точка перетину висот (ортоцентр) трикутника, точка перетину бісектрис (інцентр) трикутника, точка перетину серединних перпендикулярів до сторін трикутника, точка перетину симедіан (точка Лемуана) трикутника, точка Брокара, точка Ферма, точка Нагеля, точка Жаргонна, точка Торічеллі тощо. Серед нещодавно відкрити точок можна назвати точку Іффа, точку Аджима-Мальфатті, точку Аполлоніуса, точку Гофштадтера та деякі інші.
В даній роботі розглядаються найвідоміші чудові (визначні) точки трикутника, а саме: точка перетину медіан (центроїд) трикутника, точка перетину висот (ортоцентр) трикутника, точка перетину бісектрис (інцентр) трикутника, точка перетину серединних перпендикулярів до сторін трикутника, точка перетину симедіан (точка Лемуана) трикутника.
Для кожної з вказаних точок дається алгоритм її побудови за допомогою лінійки та циркуля, а також проводиться дослідження основних властивостей. Для більшості властивостей чудових (визначних) точок трикутника наведене доведення (інколи декількома способами), а також дані приклади розв’язування задач з використання вказаних властивостей.
Робота може слугувати початковим етапом для ґрунтовнішого дослідження чудових (визначних) точок трикутника.
РОЗДІЛ 1
ТОЧКА ПЕРЕТИНУ МЕДІАН ТРИКУТНИКА
Означення 1.1
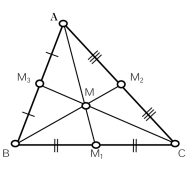
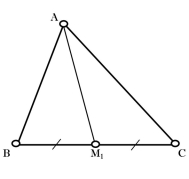
Медіана трикутника – це відрізок, який з'єднує вершину трикутника з серединою протилежної сторони.

Рис. 1.1 Рис. 1.2
Відрізок ![]() – медіана трикутника
– медіана трикутника ![]()
![]() (рис. 1.1). Будь-який трикутник має три медіани, які перетинаються в одній точці. Відрізки
(рис. 1.1). Будь-який трикутник має три медіани, які перетинаються в одній точці. Відрізки ![]() ,
, ![]() і
і ![]() – медіани трикутника
– медіани трикутника ![]() (рис. 1.2).
(рис. 1.2).
Означення 1.2
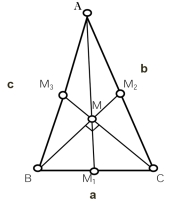
Медіани трикутника перетинаються в одній точці. Точка перетину медіан трикутника називається центроїдом трикутника.
- Побудова точки перетину медіан (центроїда) трикутника
Для побудови точки перетину медіан трикутника необхідно:
– знайти середину сторони трикутника:
– побудувати кола з центрами в точках ![]() та
та ![]() довільного радіуса
довільного радіуса ![]() ;
;
– з’єднати точки перетину кіл ![]() між собою (рис. 1.3);
між собою (рис. 1.3);
– точка ![]() перетину відрізків
перетину відрізків ![]() та
та ![]() є серединою відрізка
є серединою відрізка ![]() .
.
– з’єднати точку ![]() з вершиною
з вершиною ![]() :
: ![]() медіана трикутника (рис. 1.4);
медіана трикутника (рис. 1.4);
– подібним чином знайти іншу медіану трикутника;
– точка перетину медіан і є центроїд трикутника (рис. 1.5).
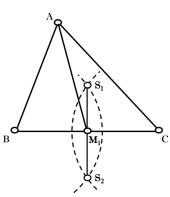
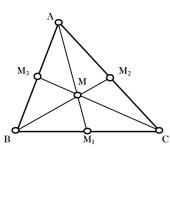
Рис. 1.3 Рис. 1.4 Рис. 1.5
- Властивості точки перетину медіан (центроїда) трикутника
Властивість 1.1
Медіани трикутника перетинаються в одній точці. Точка перетину медіан трикутника поділяє кожну медіану у відношенні 2:1, починаючи від вершини.
|
Д а н о:
Д о в е с т и:
Д о в е д е н н я 1 (рис. 1.6):
Через точку |
Рис. 1.6 |
Точку її перетину зі стороною ![]() позначимо
позначимо ![]() .
.
Тоді ![]() – середина
– середина ![]() (
(![]() – середня лінія
– середня лінія ![]() ).
).
Маємо, ![]() .
.
За теоремою Фалеса отримуємо: ![]() , тобто: медіани
, тобто: медіани ![]() і
і ![]() перетинаються в точці
перетинаються в точці ![]() , яка ділить медіану
, яка ділить медіану ![]() у відношенні 2:1.
у відношенні 2:1.
Аналогічно, медіана ![]() перетинає медіану
перетинає медіану ![]() в точці, яка ділить медіану
в точці, яка ділить медіану ![]() у відношенні 2:1, тобто в точці
у відношенні 2:1, тобто в точці ![]() .
.
|
Д о в е д е н н я 2 (рис. 1.7):
Знайдемо середини
Розглянемо чотирикутник
Його сторони
середні лінії
Отже чотирикутник
Враховуючи, що |
Рис. 1.7 |
![]() , а значить,
, а значить, ![]() .
.
Також ![]() .
.
Залишаться довести, що медіани перетинаються в одній точці.
Властивість 1.2
Якщо з’єднати точку перетину медіан (центроїд) трикутника з його вершинами, то отримаємо три рівновеликі за площею трикутники.
|
Д а н о:
Д о в е с т и:
Д о в е д е н н я: Доведемо два проміжні твердження.
|
Рис. 1.8 |
1. Медіана поділяє трикутник на два рівних за площею трикутники.
|
Д а н о:
Д о в е с т и:
Д о в е д е н н я:
Оскільки
|
Рис. 1.9 |
2. Три медіани поділяють трикутник на шість рівних за площею трикутників.
|
Д а н о:
Д о в е с т и:
Д о в е д е н н я:
|
Рис. 1.10 |
Проте ![]() та
та ![]() складаються з двох рівних за площею трикутників.
складаються з двох рівних за площею трикутників.
Тобто всі шість трикутників мають однакову площу.
Отже, ми довели властивість 1.2: ![]() .
.
Властивість 1.3
Точка перетину медіан (центроїд) трикутника є його центром тяжіння або центром мас.
|
Д а н о:
Д о в е с т и:
Д о в е д е н н я (запропоноване Архімедом): Скористаємося інтуїтивно зрозумілими і такими, які мають простий механічний зміст, властивостями центру мас: |
Рис. 1.11 |
– усяка система скінченого числа матеріальних точок має центр мас і притому єдиний;
– центр мас двох матеріальних точок розташований на відрізку, який з’єднує ці точки; його положення визначається правилом важеля Архімеда – добуток маси точки на відстань від неї до центру мас однаковий для обох точок;
– якщо в системі матеріальних точок скасувати деякі з них, а маси скасованих точок перенести в їх центр мас, то від цього положення центру мас всієї системи не зміниться.
У вершинах трикутника розмістимо кульки однакової маси (наприклад, 1). Отримана система матеріальних точок має один центр мас ![]() (властивість 1). Виходячи з властивості 3, положення центру мас не зміниться, якщо маси матеріальних точок
(властивість 1). Виходячи з властивості 3, положення центру мас не зміниться, якщо маси матеріальних точок ![]() і
і ![]() перенести в їх центр мас, тобто згідно властивості 2, в точку
перенести в їх центр мас, тобто згідно властивості 2, в точку ![]() . Тоді точка
. Тоді точка ![]() виявиться центром мас всього двох матеріальних точок
виявиться центром мас всього двох матеріальних точок ![]() і
і ![]() , тобто
, тобто ![]() . Подібним чином впевнимося, що
. Подібним чином впевнимося, що ![]() та
та ![]() . Тобто, медіани трикутника мають спільну точку
. Тобто, медіани трикутника мають спільну точку ![]() . І по правилу важеля (властивість 2) маємо:
. І по правилу важеля (властивість 2) маємо: ![]() , тобто
, тобто ![]() .
.
Властивість 1.4 (Теорема Лейбніца *)
Медіани трикутника ![]() перетинаються в точці
перетинаються в точці ![]() . Для довільної точки
. Для довільної точки ![]() площини має місце рівність:
площини має місце рівність:
![]() .
.
Ґотфрід Вільгельм Лейбніц (01.07.1646 – † 14.11.1716) – знаменитий німецький математик.
Властивість 1.5 (Наслідок теореми Лейбніца)
Точка перетину медіан (центроїд) трикутника є точкою, для якої сума квадратів відстаней до вершин трикутника має найменше значення.
Властивість 1.6
Точка перетину медіан (центроїд) трикутника є єдиною точкою трикутника, для якої сума трьох векторів, що виходять з неї до вершин трикутника, рівна нулю.
Властивість 1.7
Для будь-якого трикутника ![]() і будь-якої точки
і будь-якої точки ![]() справедливе твердження:
справедливе твердження: ![]() , де
, де ![]() – центроїд трикутника
– центроїд трикутника ![]() .
.
Властивість 1.8
Координати точки перетину медіан (центроїда) трикутника (щодо довільних осей) дорівнюють середнім арифметичним відповідних координат вершин трикутника.
Властивість 1.9
Точка перетину медіан (центроїд) трикутника при проектуванні трикутника на площину переходить в точку перетину медіан (центроїд) спроектованого трикутника.
Властивість 1.10
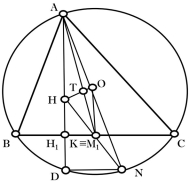
Точка перетину медіан (центроїд) трикутника лежить на відрізку, який з’єднує точку перетину висот або їх продовжень (ортоцентр) трикутника і точку перетину серединних перпендикулярів до його сторін (центр описаного навколо нього кола), і ділить його у відношенні 2:1. Пряма, на якій лежать ці три точки, називається прямою Ейлера.
- Приклади розв’язування задач
Задача 1.1
У трикутнику ![]() точка
точка ![]() є точкою перетину медіан. Знайти площу трикутника
є точкою перетину медіан. Знайти площу трикутника ![]() , якщо площа трикутника
, якщо площа трикутника ![]() дорівнює
дорівнює ![]() .
.
|
Д а н о:
З н а й т и:
Р о з в’ я з о к: |
Рис. 1.12 |
Згідно властивості 1.2 (проміжне твердження 1) – медіана будь-якого трикутника поділяє його на два рівних за площею трикутники.
Тому площа трикутника ![]() дорівнює половині
дорівнює половині ![]() :
: ![]() .
.
Лінія ![]() є медіаною трикутника
є медіаною трикутника ![]() , тому площа трикутника
, тому площа трикутника ![]() дорівнює половині площі трикутника
дорівнює половині площі трикутника ![]() (згідно тієї ж властивості), тобто:
(згідно тієї ж властивості), тобто: ![]() .
.
Так як медіани в точці перетину діляться у відношенні 2:1 (властивість 1.1), то ![]() .
.
Отже, площа трикутника ![]() дорівнює третині площі трикутника
дорівнює третині площі трикутника ![]() :
: ![]() .
.
Відповідь: ![]() .
.
Задача 1.2
На продовженні сторони ![]() трикутника
трикутника ![]() вибрано точку
вибрано точку ![]() так, що
так, що ![]() (рис. 1.13). Нехай
(рис. 1.13). Нехай ![]() – середина сторони
– середина сторони ![]() , а
, а ![]() – точка перетину
– точка перетину ![]() і
і ![]() . Довести, що трикутник
. Довести, що трикутник ![]() рівновеликий чотирикутнику
рівновеликий чотирикутнику ![]() . (Всеукраїнська олімпіада, 1985 рік).
. (Всеукраїнська олімпіада, 1985 рік).
|
Д а н о:
Д о в е с т и:
Д о в е д е н н я:
Згідно властивості 1.2 (проміжне твердження 2) – медіани трикутника, які перетинаються в точці
|
Рис. 1.13
Рис. 1.14 |
Задача 1.3
У трикутнику ![]() (рис. 1.15) медіани
(рис. 1.15) медіани ![]() і
і ![]() перпендикулярні, тобто
перпендикулярні, тобто ![]() . Довести, що в трикутнику
. Довести, що в трикутнику ![]()
![]() .
.
|
Д а н о:
Д о в е с т и:
Д о в е д е н н я:
Дійсно, |
Рис. 1.15 |
РОЗДІЛ 2
ТОЧКА ПЕРЕТИНУ ВИСОТ ТРИКУТНИКА
Означення 2.1
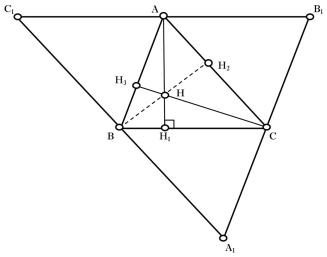
Висота трикутника - відрізок, проведений з вершини трикутника до протилежної сторони або до продовження протилежної сторони і лежить на прямій, перпендикулярній до цієї сторони.
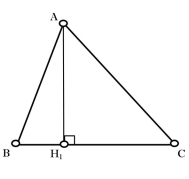
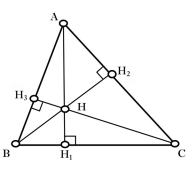
Рис. 2.1 Рис. 2.2
Відрізок ![]() – висота трикутника
– висота трикутника ![]()
![]() ,
, ![]() – основа висоти (рис. 2.1). Будь-який трикутник має три висоти, які перетинаються в одній точці. Відрізки
– основа висоти (рис. 2.1). Будь-який трикутник має три висоти, які перетинаються в одній точці. Відрізки ![]() ,
, ![]() і
і ![]() – висоти трикутника
– висоти трикутника ![]() (рис. 2.2).
(рис. 2.2).
Означення 2.2
Три висоти трикутника перетинаються в одній точці. Ця точка називається ортоцентром трикутника.
2.1. Побудова точки перетину висот (ортоцентру) трикутника
Для побудови точки перетину висот (ортоцентру) трикутника необхідно:
– побудувати висоту трикутника:
– побудувати коло з центрам в точці ![]() радіусом
радіусом ![]() ;
;
– побудувати коло з центрам в точці ![]() радіусом
радіусом ![]() ;
;
– з’єднати точку перетину кіл ![]() з вершиною
з вершиною ![]() (рис. 2.3);
(рис. 2.3);
– знайти точку ![]() перетину відрізків
перетину відрізків ![]() та
та ![]() ;
;
– ![]() є висотою трикутника
є висотою трикутника ![]() (рис. 2.4).
(рис. 2.4).
– аналогічно побудувати висоти трикутника ![]() та
та ![]() (рис. 2.5).
(рис. 2.5).
Зауваження 2.1. Ортоцентр лежить всередині трикутника (відповідно основи перпендикулярів лежать у трикутнику) тоді і тільки тоді, якщо трикутник не тупокутний.
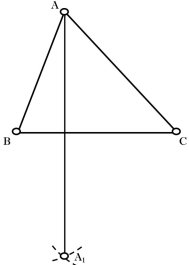
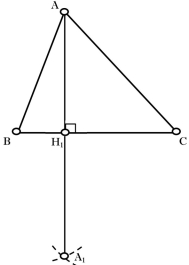
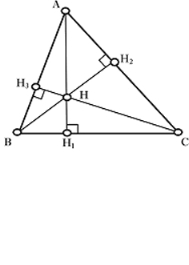
Рис. 2.3 Рис. 2.4 Рис. 2.5
2.2. Властивості точки перетину висот (ортоцентра) трикутника
Властивість 2.1
Висоти трикутника перетинаються в одній точці.
|
Д а н о:
Д о в е с т и:
Д о в е д е н н я:
Через вершини трикутника |
Рис. 2.6 |
![]() .
.
![]() (як протилежні сторони паралелограма
(як протилежні сторони паралелограма ![]() ),
),
![]() (як протилежні сторони паралелограма
(як протилежні сторони паралелограма ![]() ).
).
Звідси маємо, що ![]() .
.
Аналогічно доводиться, що ![]() та
та ![]() .
.
Крім того, відомо, що ![]() та
та ![]() .
.
Отже, ![]() – точка перетину серединних перпендикулярів трикутника
– точка перетину серединних перпендикулярів трикутника ![]() .
.
Оскільки точка ![]() є серединою відрізка
є серединою відрізка ![]() , то
, то ![]() (а, отже,
(а, отже, ![]() ) і
) і ![]() є третьою висотою для трикутника
є третьою висотою для трикутника ![]() .
.
Властивість 2.2
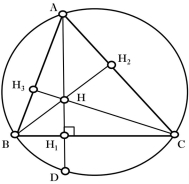
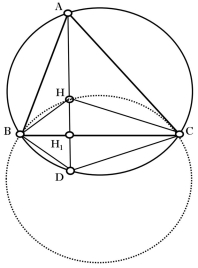
Точки, симетричні ортоцентру відносно сторін трикутника, належать описаному навколо трикутника колу.
|
Д а н о:
Д о в е с т и:
Д о в е д е н н я: (рис. 2.7) |
Рис. 2.7 |
![]() (з
(з ![]() ).
).
![]() (вертикальні кути).
(вертикальні кути).
![]() (згідно з міркуваннями симетрії). Отже:
(згідно з міркуваннями симетрії). Отже: ![]() .
.
Оскільки сума протилежних кутів чотирикутника ![]() дорівнює
дорівнює ![]() , то цей чотирикутник є вписаним, а це рівнозначно тому, що точка
, то цей чотирикутник є вписаним, а це рівнозначно тому, що точка ![]() належить описаному навколо трикутника
належить описаному навколо трикутника ![]() колу.
колу.
Аналогічно ця властивість доводиться для двох інших сторін.
Зауваження 2.2. У випадку тупокутного трикутника ![]() дана властивість зберігається, незважаючи на те, що ортоцентр вийде за межі трикутника.
дана властивість зберігається, незважаючи на те, що ортоцентр вийде за межі трикутника.
Властивість 2.3 (Властивість 1.10)
Точка перетину медіан (центроїд) трикутника лежить на відрізку, який з’єднує точку перетину висот або їх продовжень (ортоцентр) трикутника і точку перетину серединних перпендикулярів до його сторін (центр описаного навколо нього кола), і ділить його у відношенні 2:1. Пряма, на якій лежать ці три точки, називається прямою Ейлера.
|
Д а н о:
Д о в е с т и:
Точки
причому |
Рис. 2.8 |
Д о в е д е н н я:
Продовжимо висоту ![]() до перетину з описаним колом.
до перетину з описаним колом.
Точка ![]() симетрична ортоцентру
симетрична ортоцентру ![]() відносно сторони
відносно сторони ![]() .
.
Проведемо ![]() . З’єднаємо
. З’єднаємо ![]() з
з ![]() .
. ![]() – діаметр, бо
– діаметр, бо ![]() .
.
Отже, ![]() проходить через точку
проходить через точку ![]() і ця точка ділить
і ця точка ділить ![]() навпіл.
навпіл.
З’єднаємо ![]() з
з ![]() .
. ![]() перетне
перетне ![]() у деякій точці
у деякій точці ![]() . З’єднаємо
. З’єднаємо ![]() з
з ![]() .
.
Оскільки ![]()
![]() і
і![]() , то
, то ![]() і
і ![]() (середня лінія). Звідси маємо, що
(середня лінія). Звідси маємо, що ![]() збігається з
збігається з ![]() .
.
Тепер розглянемо ![]() . У ньому
. У ньому ![]() і
і ![]() є медіанами.
є медіанами.
Оскільки медіани трикутника у точці перетину діляться у відношенні ![]() , починаючи від вершини, а
, починаючи від вершини, а ![]() – точка їх перетину, то
– точка їх перетину, то ![]() .
.
Але оскільки ![]() є також медіаною трикутника
є також медіаною трикутника ![]() , то очевидно,
, то очевидно, ![]() . Отже, точки
. Отже, точки ![]() ,
, ![]() ,
, ![]() належить одній прямій та ще й
належить одній прямій та ще й ![]() .
.
Властивість 2.4
Точки, симетричні ортоцентру відносно середин сторін трикутника, належать описаному навколо трикутника колу.
|
Д а н о:
Д о в е с т и:
Д о в е д е н н я: |
Рис. 2.9 |
З точки ![]() опустимо перпендикуляр на сторону
опустимо перпендикуляр на сторону ![]() .
.
![]() – основа перпендикуляра.
– основа перпендикуляра. ![]() .
.
![]()
![]() (за гіпотенузою і гострим кутом). Отже,
(за гіпотенузою і гострим кутом). Отже, ![]() .
.
![]()
![]() (за стороною, медіаною і висотою). Отже,
(за стороною, медіаною і висотою). Отже, ![]() .
.
З чотирикутника ![]() знайдемо
знайдемо ![]() :
:
![]() .
.
Маємо: ![]() (вертикальні кути).
(вертикальні кути).
Оскільки ![]() , то
, то ![]() .
.
Розглянемо чотирикутник ![]() : сума протилежних кутів
: сума протилежних кутів ![]() , отже він є вписаним. Значить, точка
, отже він є вписаним. Значить, точка ![]() належить описаному навколо
належить описаному навколо ![]() колу. Аналогічно властивість доводиться для двох інших сторін трикутника.
колу. Аналогічно властивість доводиться для двох інших сторін трикутника.
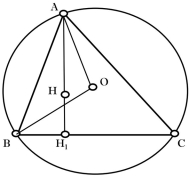
Властивість 2.5
Відрізки, які з’єднують вершину трикутника з його ортоцентром та центром описаного кола утворюють рівні кути з бічними сторонами трикутника.
Д а н о:
![]() ;
; ![]() – висота трикутника;
– висота трикутника;
![]() – ортоцентр трикутника;
– ортоцентр трикутника;
![]() – центр описаного кола (рис. 2.10).
– центр описаного кола (рис. 2.10).
Д о в е с т и:
![]() .
.
|
Д о в е д е н н я:
З трикутника
Отже,
Трикутник
Звідси маємо, що
|
Рис. 2.10 |
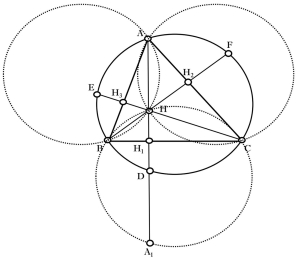
Властивість 2.6
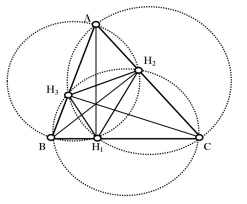
З чотирьох точок ![]() ,
, ![]() ,
, ![]() і
і ![]() (де
(де ![]() ,
, ![]() ,
, ![]() – вершини трикутника
– вершини трикутника ![]() , а
, а ![]() – ортоцентр цього трикутника) кожну з них можна розглядати як ортоцентр трикутника, утвореного трьома іншими.
– ортоцентр цього трикутника) кожну з них можна розглядати як ортоцентр трикутника, утвореного трьома іншими.
|
Д а н о:
Д о в е с т и:
Д о в е д е н н я: Маємо чотири варіанти трикутників: |
Рис. 2.11 |
(1) ![]() з ортоцентром
з ортоцентром ![]() – дано за умовою;
– дано за умовою;
(2) ![]() з ортоцентром
з ортоцентром ![]() ;
;
(3) ![]() з ортоцентром
з ортоцентром ![]() ;
;
(4) ![]() з ортоцентром
з ортоцентром ![]() .
.
Доведемо варіант (2) – варіанти (3) та (4) доводяться аналогічно:
(2) Тут ![]() – продовження сторони
– продовження сторони ![]() ,
,
![]() – продовження сторони
– продовження сторони ![]() ,
,
![]() – висота на
– висота на ![]() ,
, ![]() – висота на
– висота на ![]() .
.
![]() – висота на
– висота на ![]() .
.
Доведено.
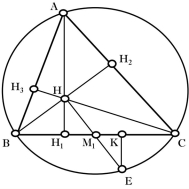
Властивість 2.7
Якщо коло, описане навколо трикутника ![]() , дзеркально відобразити відносно сторін трикутника, то отримані три кола перетнуться в ортоцентрі трикутника.
, дзеркально відобразити відносно сторін трикутника, то отримані три кола перетнуться в ортоцентрі трикутника.
|
Д а н о:
Д о в е с т и:
Д о в е д е н н я:
Нехай |
Рис. 2.12 |
відповідно сторін ![]() ,
, ![]() ,
, ![]() .
.
Доведемо, що коло, дзеркально відображене відносно сторони ![]() , пройде через ортоцентр трикутника
, пройде через ортоцентр трикутника ![]() – точку
– точку ![]() .
.
Знаючи, що точка ![]() , симетрична ортоцентру відносно сторони
, симетрична ортоцентру відносно сторони ![]() , належить описаному навколо трикутника
, належить описаному навколо трикутника ![]() колу, можемо сказати, що точка
колу, можемо сказати, що точка ![]() буде ортоцентром трикутника, дзеркально відображеного відносно сторони
буде ортоцентром трикутника, дзеркально відображеного відносно сторони ![]() (на рис. 2.12 трикутник
(на рис. 2.12 трикутник ![]() ). А точка
). А точка ![]() буде для цього трикутника точкою, симетричною ортоцентру
буде для цього трикутника точкою, симетричною ортоцентру ![]() відносно його сторони
відносно його сторони ![]() , і, отже, коло, описане навколо трикутника
, і, отже, коло, описане навколо трикутника ![]() , пройде через точку
, пройде через точку ![]() .
.
Аналогічно доводиться, що два інших кола також пройдуть через точку ![]() .
.
Отже, всі три кола перетинаються в точці ![]() .
.
Властивість 2.8
Прямі, симетричні відносно сторін трикутника довільній прямій, яка проведена через ортоцентр трикутника, перетинаються в одній точці на описаному навколо трикутника колі.
Означення 2.3
Чевіа́на - будь-який відрізок, що сполучає вершину трикутника та одну з точок на протилежній їй стороні.
Властивість 2.9
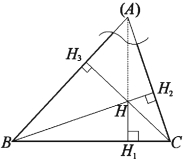
Якщо три чевіани, проведені з вершин трикутника, перетнулися в одній точці і утворили рівні кути так, як показано на рис. 2.13, то ці три чевіани є висотами, а точка їх перетину збігається з ортоцентром трикутника.
|
Д а н о:
Д о в е с т и:
Д о в е д е н н я:
Позначимо рівні кути через |
Рис. 2.13 |
Оскільки сума кутів трикутника дорівнює ![]() , то
, то ![]() .
.
Звідси: ![]() .
.
Розглянемо трикутник ![]() :
: ![]() .
.
Отже, ![]() – висота трикутника
– висота трикутника ![]() , проведена до сторони
, проведена до сторони ![]() .
.
Аналогічно доводиться, що ![]() та
та ![]() – висоти трикутника
– висоти трикутника ![]() .
.
Отже, точка їх перетину – точка ![]() – збігається з ортоцентром трикутника
– збігається з ортоцентром трикутника ![]() .
.
Властивість 2.10
Радіуси описаних кіл навколо трикутників ![]() ,
, ![]() ,
, ![]() та
та ![]() рівні.
рівні.
|
Д а н о:
Д о в е с т и:
Д о в е д е н н я:
Нехай
Доведемо, що
Маємо: |
Рис. 2.14 |
А оскільки ![]() , то
, то ![]() .
.
Аналогічно доводиться, що ![]() та
та ![]() .
.
2.3. Приклади розв’язування задач
Задача 2.1
Чи існує трикутник, в якому ортоцентр збігається з його вершиною?
Р о з в ’ я з о к:
Катети прямокутного трикутника – це також і висоти даного трикутника. Оскільки вони перетинаються у вершині прямого кута, то й висоти проходять через цю вершину. Тому вершина прямого кута в прямокутному трикутнику є його ортоцентром.
Задача 2.2 (Якоба Штейнера)
На відрізку ![]() як на діаметрі побудовано півколо з невідомим центром. Всередині півкола дано точку
як на діаметрі побудовано півколо з невідомим центром. Всередині півкола дано точку ![]() . За допомогою однієї лінійки проведіть з точки
. За допомогою однієї лінійки проведіть з точки ![]() перпендикуляр до
перпендикуляр до ![]() .
.
|
Д а н о:
Р о з в ’ я з о к:
Проведемо промені
З’єднаємо
Тоді
Продовжимо |
Рис. 2.15 |
Тоді ![]() і
і ![]() – висоти в трикутнику
– висоти в трикутнику ![]() , а точка
, а точка ![]() – його ортоцентр.
– його ортоцентр.
Пряма ![]() містить третю висоту трикутника
містить третю висоту трикутника ![]() і буде перпендикулярною до
і буде перпендикулярною до ![]() .
.
Задача 2.3
Вершина гострого кута ![]() трикутника
трикутника ![]() недоступна. Проведіть пряму, яка містить висоту
недоступна. Проведіть пряму, яка містить висоту ![]() .
.
|
Д а н о:
Р о з в ’ я з о к:
Проведемо висоти
|
Рис. 2.16 |
РОЗДІЛ 3
ТОЧКА ПЕРЕТИНУ БІСЕКТРИС ТРИКУТНИКА
Означення 3.1
Бісектриса кута - промінь, що проходить через вершину кута і ділить його навпіл. Кожна точка бісектриси однаково віддалена від сторін кута. Бісектриса трикутника - відрізок бісектриси одного з кутів цього трикутника від вершини кута до перетину з протилежною стороною.
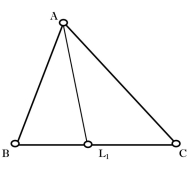
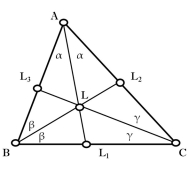
Рис. 3.1 Рис. 3.2
Відрізок ![]() – бісектриса трикутника
– бісектриса трикутника ![]()
![]() ,
, ![]() – основа бісектриси (рис. 3.1). Будь-який трикутник має три бісектриси, які перетинаються в одній точці. Відрізки
– основа бісектриси (рис. 3.1). Будь-який трикутник має три бісектриси, які перетинаються в одній точці. Відрізки ![]() ,
, ![]() і
і ![]() – бісектриси трикутника
– бісектриси трикутника ![]() (рис. 3.2).
(рис. 3.2).
Означення 3.2
Бісектриси внутрішніх кутів трикутника перетинаються в одній точці – інцентрі – центрі вписаного в цей трикутник кола.
3.1. Побудова точки перетину бісектрис (інцентру) трикутника
Для побудови точки перетину бісектрис (інцентру) трикутника необхідно:
– побудувати бісектрису кута трикутника:
– побудувати коло з центрам в точці ![]() довільного радіуса;
довільного радіуса;
– знайти точки перетину кола з сторонами ![]() та
та ![]() (рис. 3.3);
(рис. 3.3);
– зі знайдених точок як центрів побудувати два кола однакового радіуса;
– знайти точку перетину цих кіл;
– з’єднати знайдену точку з вершиною ![]() ;
;
– знайти бісектрису ![]() (рис. 3.4);
(рис. 3.4);
аналогічно побудувати бісектриси трикутника ![]() та
та ![]() (рис. 3.5).
(рис. 3.5).

Рис. 3.3 Рис. 3.4 Рис. 3.5
3.2. Властивості точки перетину бісектрис (інцентру) трикутника
Властивість 3.1
Бісектриси трикутника перетинаються в одній точці в середині трикутника.
|
Д а н о:
Д о в е с т и:
Д о в е д е н н я: Оскільки бісектриса – це геометричне місце точок, однаково віддалених від відповідних сторін трикутника, маємо: |
Рис. 3.6 |
точка ![]() – однаково віддалена від сторін
– однаково віддалена від сторін ![]() та
та ![]() трикутника
трикутника ![]() ;
;
точка ![]() – однаково віддалена від сторін
– однаково віддалена від сторін ![]() та
та ![]() трикутника
трикутника ![]() ;
;
Отже, точка ![]() однаково віддалена від сторін
однаково віддалена від сторін ![]() та
та ![]() трикутника
трикутника ![]() ;
;
Значить, ![]() , де
, де ![]() – бісектриса трикутника
– бісектриса трикутника ![]() .
.
Властивість 3.2 (Наслідок властивості 3.1)
Точка перетину бісектрис (інцентр) трикутника є центром вписаного кола.
|
Д а н о:
Д о в е с т и:
Д о в е д е н н я:
Точка |
Рис. 3.7 |
Властивість 3.3
Кожна бісектриса трикутника ділиться точкою перетину бісектрис у відношенні суми довжин прилеглих сторін до довжини протилежної, рахуючи від вершини.
|
Д а н о:
Д о в е с т и:
Д о в е д е н н я (рис. 3.8): |
Рис. 3.8 |
Скористаємось властивістю бісектриси трикутника: будь-яка бісектриса трикутника ділить протилежну сторону на відрізки, пропорційні прилеглим сторонам трикутника.
Маємо: ![]() (з трикутника
(з трикутника ![]() ,
, ![]() – бісектриса);
– бісектриса);
![]() (з трикутника
(з трикутника ![]() ,
, ![]() – бісектриса).
– бісектриса).
Отже: ![]() , або
, або ![]() .
.
Звідси: ![]() , або
, або ![]() .
.
Аналогічне доведення маємо для двох інших бісектрис трикутника.
Властивість 3.4
Пряма, що проходить через точку перетину бісектрис (інцентр) трикутника, поділяє площу і периметр в одному і тому самому відношенні.
Властивість 3.5
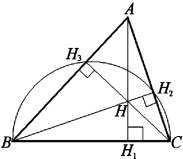
Основи висот трикутника утворюють ортоцентричний трикутник, де висоти є бісектрисами його кутів.
|
Д а н о:
Д о в е с т и:
Д о в е д е н н я (рис. 3.9):
На сторонах
Вони пройдуть через точки |
|
Кут ![]() рівний куту
рівний куту ![]() як кути, які спираються на одну дугу
як кути, які спираються на одну дугу ![]() .
.
Кут ![]() рівний куту
рівний куту ![]() (трикутники
(трикутники ![]() та
та ![]() подібні).
подібні).
Кут ![]() рівний куту
рівний куту ![]() як кути, які спираються на одну дугу
як кути, які спираються на одну дугу ![]() .
.
Отже, кут ![]() рівний куту
рівний куту ![]() .
.
3.3. Приклади розв’язування задач
Задача 3.1
Бічна сторона рівнобедреного трикутника точкою дотику вписаного кола ділиться у відношенні 8 : 9, рахуючи від вершини кута при основі трикутника. Знайдіть площу трикутника, якщо радіус вписаного кола дорівнює 16 см.
|
Д а н о:
З н а й т и:
Р о з в ’ я з о к:
Оскільки За властивістю дотичних, враховуючи симетрію |
Рис. 3.10 |
рівнобедреного трикутника, маємо: ![]() ;
; ![]() .
.
За теоремою Піфагора для трикутника ![]() маємо співвідношення:
маємо співвідношення:
![]() .
.
Звідси отримуємо: ![]() , а, отже,
, а, отже, ![]() .
.
Враховуючи те, що центр кола є точкою перетину бісектрис, за властивістю бісектриси трикутника маємо: ![]() .
.
Так як ![]() см, то
см, то ![]() см., а
см., а ![]() (см).
(см).
З умови ![]() см. отримуємо:
см. отримуємо: ![]() (см).
(см).
Основа трикутника ![]()
![]() (см).
(см).
Тоді площа вказаного трикутника буде дорівнювати:
![]() (см2).
(см2).
Задача 3.2
![]() – точка перетину бісектрис
– точка перетину бісектрис ![]() i
i ![]() трикутника
трикутника ![]() . Знайти кут
. Знайти кут ![]() , якщо кут
, якщо кут ![]() .
.
|
Д а н о:
З н а й т и:
Р о з в ’ я з о к:
|
Рис. 3.11 |
Так як ![]() і
і ![]() – бісектриси, то
– бісектриси, то ![]() .
.
Отже, ![]() .
.
Задача 3.3
Довести, що кут між бісектрисами гострих кутів прямокутного трикутника завжди один і той самий.
|
Д а н о:
Д о в е с т и:
Д о в е д е н н я: |
Рис. 3.12 |
Оскільки ![]() , то
, то ![]() і
і ![]() .
.
Задача 3.4
Через точку ![]() перетину бісектрис трикутника
перетину бісектрис трикутника ![]() проведено пряму, яка відтинає від нього трикутник
проведено пряму, яка відтинає від нього трикутник ![]() . Доведіть, що
. Доведіть, що ![]() , де
, де ![]() - радіус вписаного в
- радіус вписаного в ![]() кола.
кола.
|
Д а н о:
Д о в е с т и:
Д о в е д е н н я: Розв’яжемо спочатку проміжну задачу. |
Рис. 3.13 |
Дано кут ![]() і довільна точка
і довільна точка ![]() всередині нього. Провести через
всередині нього. Провести через ![]() пряму в такий спосіб, щоби вона відтинала від сторін кута трикутник мінімальної площі.
пряму в такий спосіб, щоби вона відтинала від сторін кута трикутник мінімальної площі.
|
Д а н о:
Р о з в ’ я з о к:
Відповіддю до цієї задачі буде трикутник |
Рис. 3.14 |
більшу ніж ![]() , точно на «шматочок», який
, точно на «шматочок», який
заштриховано на малюнку.
Цей «шматочок» буде рівним нулю, коли ![]() .
.
Тепер розв’яжемо основну задачу.
З усіх можливих трикутників ![]() розглянемо той, який має найменшу площу. За проміжною задачею в ньому
розглянемо той, який має найменшу площу. За проміжною задачею в ньому ![]() , тобто цей трикутник – рівнобедрений.
, тобто цей трикутник – рівнобедрений.
Проведемо перпендикуляр ![]() до сторони
до сторони ![]() , який дорівнює
, який дорівнює ![]() .
.
Трикутники ![]() і
і ![]() подібні за двома кутами. В трикутнику
подібні за двома кутами. В трикутнику ![]() :
: 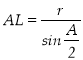 .
.
В трикутнику ![]() :
: 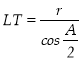 .
.
Тоді формула ![]() матиме вигляд:
матиме вигляд: 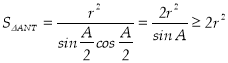 . (зауважимо, що знак рівності має місце, коли
. (зауважимо, що знак рівності має місце, коли ![]() і
і ![]() ).
).
РОЗДІЛ 4
ТОЧКА ПЕРЕТИНУ СЕРЕДИННИХ ПЕРПЕНДИКУЛЯРІВ
ДО СТОРІН
Означення 4.1
Серединний перпендикуляр до сторони трикутника – це пряма, що проходить через середину цієї сторони, перпендикулярно до неї. Інакше: геометричне місце точок, що знаходяться на однаковій відстані від вершин трикутника.
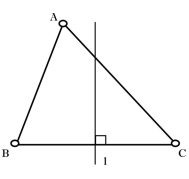
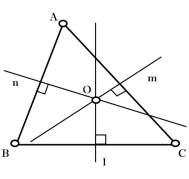
Рис. 4.1 Рис. 4.2
Пряма ![]() – серединний перпендикуляр до сторони
– серединний перпендикуляр до сторони ![]() (рис. 4.1). Три серединні перпендикуляри перетинаються в одній точці (рис. 4.2).
(рис. 4.1). Три серединні перпендикуляри перетинаються в одній точці (рис. 4.2).
Означення 4.2
Серединні перпендикуляри до сторін трикутника перетинаються в одній точці. Точка перетину серединних перпендикулярів до сторін трикутника є центром описаного навколо цього трикутника кола.
4.1. Побудова точки перетину серединних перпендикулярів
до сторін
Для побудови точки перетину серединних перпендикулярів необхідно:
– побудувати серединний перпендикуляр до сторони трикутника:
– побудувати кола однакового радіусу з центрами в двох вершинах
![]() і
і ![]() трикутника так, щоб
трикутника так, щоб ![]() >
> ![]() (рис. 4.3);
(рис. 4.3);
– з’єднати точки перетину кіл ![]() між собою (рис. 4.4);
між собою (рис. 4.4);
– подібним чином знайти інший серединний перпендикуляр трикутника;
– знайти точка перетину серединних перпендикулярів (рис. 4.5).
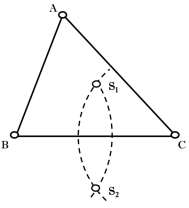
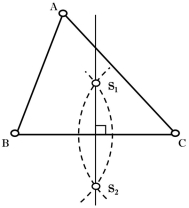
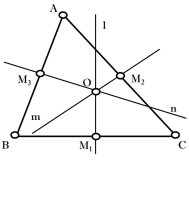
Рис. 4.3 Рис. 4.4 Рис. 4.5
4.2. Властивості точки перетину серединних перпендикулярів
Властивість 4.1
Серединні перпендикуляри до сторін трикутника перетинаються в одній точці.
|
Д а н о:
Д о в е с т и:
Д о в е д е н н я:
|
Рис. 4.6 |
Отже, ![]() точка
точка ![]() рівновіддалена від вершин
рівновіддалена від вершин ![]() і
і ![]() , а, значить, лежить на серединному перпендикулярі до сторони
, а, значить, лежить на серединному перпендикулярі до сторони ![]() .
.
Властивість 4.2
Точка перетину серединних перпендикулярів до сторін трикутника є центром кола, описаного навколо цього трикутника.
|
Д а н о:
Д о в е с т и:
Д о в е д е н н я: |
Рис. 4.7 |
Оскільки точка ![]() рівновіддалена від всіх вершин трикутника, то
рівновіддалена від всіх вершин трикутника, то ![]() – радіус описаного навколо трикутника кола.
– радіус описаного навколо трикутника кола.
Властивість 4.3
Центр описаного навколо трикутника кола служить ортоцентром трикутника з вершинами на серединах сторін даного трикутника.
|
Д а н о:
Д о в е с т и:
|
Рис. 4.8 |
Д о в е д е н н я:
![]() – середня лінія трикутника
– середня лінія трикутника ![]() , а, значить,
, а, значить, ![]() – висота трикутника
– висота трикутника ![]() .
.
Аналогічно, ![]() – висота трикутника
– висота трикутника ![]() .
.
Точка ![]() – точка перетину висот трикутника
– точка перетину висот трикутника ![]() , а, отже, його ортоцентр.
, а, отже, його ортоцентр.
РОЗДІЛ 5
ТОЧКА ПЕРЕТИНУ СИМЕДІАН ТРИКУТНИКА (ТОЧКА ЛЕМУАНА)
Означення 5.1
Симедіана – чевіана трикутника, промінь якої симетричний променю медіани щодо бісектриси кута, проведеної з тієї ж вершини.
Означення 5.2
Симедіани трикутника перетинаються в одній точці. Точка перетину симедіан трикутника називається точкою Лемуана*.
* Еміль Лемуан (1840 – † 1912), французький математик який вперше присвятив точці перетину симедіан трикутника ряд досліджень.
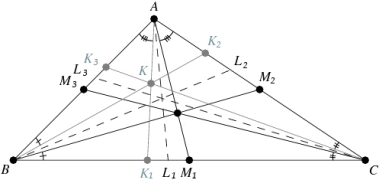
Рис. 5.1
Відрізок ![]() ,
,![]() ,
,![]() – симедіани трикутника
– симедіани трикутника ![]() . Три симедіани трикутника перетинаються в одній точці
. Три симедіани трикутника перетинаються в одній точці ![]() (рис. 5.1).
(рис. 5.1).
5.1. Властивості точки перетину симедіан трикутника
Властивість 5.1
Симедіани трикутника перетинаються в одній точці, яка називається точкою Лемуана.
Властивість 5.2
Сума квадратів відстаней від точки на площині до сторін трикутника мінімальна, коли ця точка є точкою Лемуана.
Властивість 5.3
Відстані від точки Лемуана до сторін трикутника пропорційні довжинам сторін.
Властивість 5.4
Точка Лемуана є точкою перетину медіан трикутника, утвореного проекціями точки Лемуана на сторони. Більше того, така точка є єдиною.
Властивість 5.5 (Паралелі Лемуана)
Нехай є трикутник ![]() з точкою Лемуана
з точкою Лемуана ![]() . Відрізки прямих, що проходять через
. Відрізки прямих, що проходять через ![]() паралельно до сторін трикутника, називаються паралелями Лемуана. Шість точок перетину цих відрізків та сторін трикутника лежать на одному колі, яке називається першим колом Лемуана (рис. 5.2).
паралельно до сторін трикутника, називаються паралелями Лемуана. Шість точок перетину цих відрізків та сторін трикутника лежать на одному колі, яке називається першим колом Лемуана (рис. 5.2).
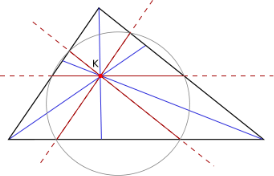
Рис. 5.2
Властивість 5.6
Точка Лемуана є точкою перетину прямих, що з'єднують кожну вершину трикутника з точками перетину дотичних до описаного кола, проведених з двох інших вершин.
ВИСНОВОК
В роботі проводилось дослідження деяких основних властивостей чудових (визначних) точок трикутник. Розглядалися наступні чудові (визначні) точки трикутника: точка перетину медіан (центроїд) трикутника, точка перетину висот (ортоцентр) трикутника, точка перетину бісектрис (інцентр) трикутника, точка перетину серединних перпендикулярів до сторін трикутника, а також точка перетину симедіан трикутника (точка Лемуана). Для кожної з вищевказаних точок трикутника сформульовані основні її властивості, для більшості з них наведені доведення (інколи декількома способами). В кінці кожного розділу наведені приклади розв’язування задач з використанням властивостей вказаних точок трикутника.
Дана робота може бути розглянута як початковий етап дослідження властивостей як вже вказаних чудових (визначних) точок трикутника, так і інших точок.
СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ
1. Александров И.И. Сборник геометриченских задач на построение [Текст] : учеб. пособ. / И.И.Александров. – 18-е изд., стер. – М. : Учпедгиз, 1950. – 176 с.
2. Бевз Г.П. Геометрія трикутника [Текст] : навч.-метод. посіб. / Г.П.Бевз. – К. : Генеза, 2005. – 128 с.
3. Вахрамєєва А.М. Чудові точки трикутника [Електронний ресурс] : курс. проект / А.М.Вахрамєєва ; М-во освіти і науки Російської Федерації, Магнітогорський державний університет. – К. : 2014. – Режим доступу: http://www.ukrbukva.net
4. Дубровский В. Шесть доказательств теоремы о медианах [Текст] / В.Дубровский // Квант. – 1978. – № 4. – С. 54-56.
5. Кушнір І.А. 101 задача про чудові точки трикутника [Текст] : І.А.Кушнір. – К. : Факт, 2007. – 160 с.
6. Смирнова И.М. Замечательные точки и линии треугольника [Електронний ресурс] : учебн.-метод. сайт / И.М.Смирнова, В.А.Смирнов. – М. : 2006. – Режим доступу: http://www.geom8klas.blogspot.com
7. Смолина Л.М. Замечательные точки треугольника [Електронний ресурс] : і-школа / Л.М.Смолина – [М.], – Режим доступу: http://www.home-edu.ru
8. Філіпповський Г. Впізнати чудову точку трикутника [Текст] / Г.Філіпповський // У світі математики. – К. : ТВІМС, 2013. – Т.19. – Вип.2. – С. 43-52.
ІНТЕРНЕТ-РЕСУРСИ
http://www.geom8klas.blogspot.com
http://www.olimpmath.blogspot.com
http://www.osvita24.com.ua
http://www.zno0432.blogspot.com
1


про публікацію авторської розробки
Додати розробку