Цікава математика софізми та парадокси

                                                    

  ЗМІСТ

 

 

ВСТУП  . ………..………………………………………………………2

Теоретична частина  …………………………………………............. 5

 1.Визначення софізма в математиці……………………………….......5

2.Визначення парадокса в математиці…………………………...…….6

Практична частина…………………………………………….……….9

1.Приклади задач – софізмів…………………………………..................9

2. Приклади задач – парадоксів…………………………………………16

ВИСНОВКИ……………………………………………………………..19

 СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ…………………….............22

 

 

 

 

 

 

 

 

 

 

 

                                                                       Вступ

 

   Тисячі шляхів ведуть до помилки,

       до істини - тільки один.

  Жан-Жак Руссо.

Всі ми схильні помилятися: свідомо чи несвідомо (навмисно). Серед них досить поширеними є логічні помилки.  Звичайно прийнято логічні помилки поділяти на дві групи: на помилки логічні у власному змісті і помилки, які відбуваються внаслідок неправильності в словесному вираженні думки. У першому випадку помилка полягає в неправильності логічного процесу, у другому в неправильності вираження. Серед свідомих помилок виділяють софізми, серед ненавмисних - паралогізми.  Софізми – свідоме порушення певних правил і законів раціонального теоретичного мислення. Всі численні види софізмів навряд чи доречно наводити, бо кожному з законів логіки, правил визначення, поділу тощо належить його перекручення. Паралогізм - (від грец. paralogismos — неправильне, помилкове міркування)  — ненавмисна логічна помилка, зв'язана з порушенням законів і правил логіки.  Паралогізми варто відрізняти від софізму — помилки, вчиненої навмисно, з метою ввести в оману опонента, обґрунтувати помилкове твердження і т.п.

 З античних часів математику вважають наукою точною, що не терпить помилок, вимагає ясності понять та тверджень, нічого не сприймає без доведень, проголошує красу та велич логічних міркувань. За словами Ж.Фабра "математика - дивовижна вчителька в мистецтві спрямовувати думки, наводити порядок там, де вони не впорядковані, викорчовувати безглуздя, фільтрувати брудне і наводити ясність".

         Процес пізнання людиною навколишнього світу можна порівняти з радісним святом, бо кожна розкрита таємниця зміцнює віру в свої сили. Але на шляху переможної людської думки виникають великі, здавалося б непереборні перешкоди, перед якими були безсилими умовиводи. Давньогрецький філософ Діодор Кронос (приблизно307 рік до н.е) не вирішивши одну з найдавніших логічних завдань - парадокс Евкліда, помер від розчарування, а інший філософ Фигет Косский, пізнавши таку ж невдачу, покінчив життя самогубством. Давньогрецькі вчені стикалися з такими завданнями в математиці. Вони докладали чимало зусиль, щоб виявити механізм утворення таких загадок. Було встановлено, що наші міркування теж підпорядковані певним законам (законами логіки), порушення яких знецінює результати, отримані в цих міркуваннях. Невирішеність завдань, з якими зустрілися Діодор Кронос і Фигет Косский, пояснюється як правило, порушенням законів логіки. Тому вже тоді гостро постало питання про систему "профілактичних прийомів" - певних правил з метою усунення логічних помилок.

        Помилки в міркуваннях, найчастіше  виникають через порушення законів формальної логіки, основи якої заклав визначний давньогрецький філософ Арістотель (праці "Категорії", "Про тулмачення", "Перша аналітика", "Друга аналітика", "Топіка"). Помилки, пов'язані з порушенням законів логіки  та законів математики бувають двох типів: паралогізми і софізми. Паралогізми (з грецької - неправильне) - це хибне міркування, логічна помилка, допущена не навмисне, а через втрату послідовності в міркуваннях чи порушення одного з законів логіки. Паралогізми в математиці неприпустимі, бо де є місце помилці, там вже немає місця математиці. Зовсім інша ситуація з софізмами. Софізми (з грецької -хитрий викрутас, вигадка, хитрий умовивід) - це міркування навмисне побудовані так, що вони містять логічну помилку і звичайно, приводять до хибних висновків. Засновником школи софістів був давньогрецький філософ Протогор із  Адбери (бл. 480   - бл.410 до р. х.). Введення софізмів сприяло вдосконавленню ораторського мистецтва, підвищенню логічної культури мислення. Щоправда, пізніше в деяких філософів-софістів мистецтво софістики перетворилося на суперечку заради суперечки. Різні приклади софізмів наводить у своїх діалогах Платон (427 -347 до р. х.). Евклід ( 1V ст. До р. х.) створив дивовижний збірник "Псевдарій", який на жаль не дійшов до нас. Це був перший збірник саме математичних софізмів та парадоксів. Вперше аналіз та класифікацію софізмів  дав Арістотель у трактаті "Про софістичні спростування". На сьогодні софізми, і зокрема математичні, навчають мислити, доводити й спростовувати, чітко висловлювати свої думки; вони здивовують та захоплюють, дають поштовх для творчості, пошуку нового, відкриттів. Найчастіше софізми та паралогізми виникають, коли міркування порушують закони логіки: закон тотожності, закон суперечності, закон виключного третього, закон достатьньої підстави.

        У наш час вчені продовжують цю  справу зовсім не для того, щоб здивувати когось. Людині властиво помилятися,  тому дуже  важливо, щоб вона  вміла виявляти свої і чужі помилки, навчатися  уникати їх. Дійсно,  чим хитріший софізм, ніж замаскованіша  помилка, тим більше задоволення приносить він тому хто розгадав його, так як це - маленьке відкриття і прекрасна школа, культура  математичних обчислень. Збірники математичних софізмів і парадоксів завжди були популярними.

 

 

 

Теоретична частина

1. Визначення софізма в математиці

    Математичний софізм — це окремий випадок помилок у математичних міркуваннях. Вони ґрунтуються на зовнішній схожості властивостей різних математичних об'єктів, дій, відношень, неправиль­ному слововживанні, неточних формулюваннях, прихованому виконанні математичних дій, на неза­конних узагальненнях при переході від скінченних до нескінченних множин об'єктів.

   З помилками в міркуваннях доводиться стикатися на кожному кроці, і уникнути їх неможливо. Більше того, процес людського пізнання полягає, по суті, з помилок - в тому числі помилок в міркуваннях - і їх виправлення. Зокрема, помилки неминучі в суперечках: якщо двоє відстоюють протилежні думки, то в силу закону протиріччя в міркуваннях, принаймні, одного з них є помилки. Софізм (буквально «майстерність, вміння, мистецтво») зазвичай визначається як умовивід або міркування, обґрунтовує якусь явну безглуздість, абсурд чи парадоксальне твердження, що суперечить загальноприйнятим уявленням. Софізми - логічно неправильні міркування, що видаються за правильні і доказові. Удавана переконливість багатьох софізмів, ілюзія їх «логічності» і «доказовості» пов'язана з добре замаскованої помилкою, з порушенням правил мови або логіки. Софізм - це обман, але обман тонкий і закамуфльований, так що його не відразу і не кожному вдається розкрити. Говорячи про уявну переконливості софізмів, давньоримський філософ Сенека порівнював їх з мистецтвом фокусників: ми не можемо сказати, як відбуваються їх маніпуляції, хоча твердо знаємо, що все робиться зовсім не так, як нам уявляється. Ф. Бекон порівнював того, хто вдається до софізмів, з лисицею, яка добре петляє, а того, хто розкриває софізми, - з гончаком, який  вміє розплутувати сліди. У звичайному і розповсюдженому розумінні софізм - це навмисний обман, заснований на порушенні правил мови та логіки. Його мета - видати неправду за істину.       Подібне ставлення до софізмів, на перший погляд, є цілком виправданим. Дійсно, навряд чи має сенс затримуватися і роздумувати над наступними міркуваннями, які є прикладами  софізмів: «Сидячий встав, хто встав, той стоїть, отже, сидячий стоїть».

  Вже багато віків математичні софізми бентежать людську думку, прокладають шлях до істини в хащах помилок, дають поштовх творчості, заманюють несподіванками, вчать логічному мисленню, привчають до красоти бездоганних доведень.

   Досліджуючи софізми різні вчені по різному висловлювалися про них. Наприклад, Л.М.Толстой зазначав, що «головна перешкода пізнанню істини є не хибність, а подібність хибності», а припустивши десь помилку можна вже доводити все, що завгодно, бо, як говорив Блез Паскаль, «істина така тендітна, що ледь тільки відступиш від неї, помилишся».

    В історії розвитку математики софізми відіграли суттєву роль. Вони сприяли підвищенню строгості математичних міркувань та більш глибокому усвідомленню понять та методів математики.

2. Визначення парадокса в математиці

   Отож бо помилки йдуть від порушень законів логіки, або інших математичних законів. Паралогізми чекають на неуважних або недостатньо натренованих у складному мистецтві міркувань. Софізми - навмисне розставлені логічні пастки. Але бувають й інші, тривожніші, справді катастрофічні ситуації в пізнавальній діяльності людини. Іноді правильні формально-логічні міркування приводять до результатів, які не узгоджуються з загальноприйнятою думкою, здаються безглуздими. Це парадокси (з грецької - несподіваний, дивовижний).

    В даний час термін парадокс міцно увійшов в нашу мову. Його можна зустріти і в наукових текстах (парадоксальний сон, парадокси природи, парадокси науки, парадокси творчості) і в повсякденному мовленні («ну це вже парадокс») і художній літературі («О скільки нам відкриттів дивних готують просвіти дух, і досвід, син помилок важких, і геній, парадоксів друг»). Тому цілком природно, що термін парадокс розуміється по-різному в різних ситуаціях.

   Таким чином, парадокс - це протиріччя, а не помилка, його появу не можна пояснити бажанням свідомо спотворити стан справ або незнанням якоїсь детальної інформації. Перші парадокси були відомі вже в глибоку давнину, існують і сучасні парадокси. Деякі з цих суперечностей  вдалося вирішити шляхом створення нових теорій, переосмислення усталених, але недосконалих законів. Інші - так і залишилися невирішеними. Вважається, що вчені ставляться до парадоксів з неприязню, їх називають «патологіями» науки і прагнуть якомога швидше їх позбутися. Однак це не завжди вдається. В даний час не існує науки, в якій би ніколи не виникало парадоксів. Їх знаходили в психології, лінгвістики, фізики і навіть в таких точних науках як логіка і математика.

В електронній енциклопедії Вікіпедії наводиться така класифікація парадоксів:

I. Логічні.

II. Невизначені.

III.Математичні.

ІV. Геометричні.

У.  Фізичні.

УІ. Хімічні.

УІI. Пов'язані з подорожами в часі.

ІХ. Філософські.

X. Економічні.

  Парадокси виникали і виникають в усіх галузях людської діяльності. Вивчення парадоксів, спроби їх розгадати й знешкодити мають не тільки теоритичний інтерес. Якщо в логіці й математиці можливі парадокси, то де гарантія, що в складну програму ЕОМ, яка керує, наприклад деякими життєвоважливими процесами, не прослизне один з них? Тоді такий парадокс може обернутися трагічними подіями в реальності.

 

 

 

 НІЯКЕ ЛЮДСЬКЕ ДОСЛІДЖЕННЯ НЕ МОЖЕ БУТИ НАЗВАНЕ ІСТИНОЮ ДОТИ, ПОКИ ВОНО НЕ ПРОЙДЕ ЧЕРЕЗ МАТЕМАТИЧНІ ДОВЕДЕННЯ.  

 Леонардо да Вінчі

 

Практична частина.

І. Приклади задач-софізмів

Математичні софізми можуть бути числові, геометричні, логічні, алгебраїчні.

1. Маса слона дорівнює масі комара.

    Доведення:

Нехай х – вага слона, у – вага комара. Позначимо їх суму 2к: х+у=2к.

 

Звідси х-2к=-у,   х=-у+2к.

 

Помножимо почленно ці нерівності:

 х²-2кх=у²-2ку.

 

Додамо до обох частин рівності к²:

 

х²-2кх+к²=у²-2ку+к²  або (х-к)²=(у-к)².

 

Звідси х-к=у-к      або    х=у.

 

Вага слона дорівнює вазі комара.

(Неправильно добутий корінь з квадрата числа )

 

2. Де помилка?

5 = 6

Розглянемо правильну числову рівність

35 + 10 – 45 = 42 +12 -54

 

Винесемо за дужки спільний множник

5 ( 7 + 2 – 9 ) = 6 ( 7 + 2 – 9 )

Поділимо обидві частини на спільний множник у лівій та правій частині.

Отримаємо

5 = 6.

(7 + 2 – 9 = 0, а на нуль ділити не можна)

 

3. 2 х 2 = 5

Нехай а= b+с, тоді

5а= 5b + 5с і 4b+4с=4а

Додавши почленно дві останні рівності, дістанемо:

4b+4с+5а=5b+5с+4а

Тепер віднявши від обох частин по 9а, матимемо:

4b+4с-4а = 5b+5с-5а, або

4(b+с-а)=5(b+с-а)

Звідки випливає, що 4=5  ДЕ ПОМИЛКА?

4. Знайди помилку !

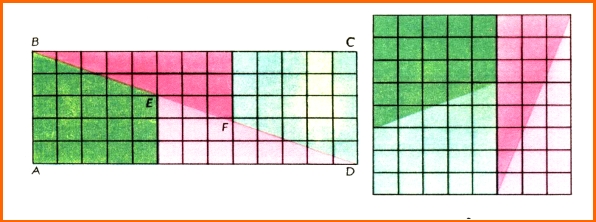   Квадрат зі стороною 8 лінійних одиниць розріжемо на частини і складемо прямокутник. Оскільки фігури складаються з однакових частин, то площі їх мають бути рівними. Однак, зробивши відповідні обчислення, бачимо, що площа квадрата дорівнює 64 кв. од. , а площа прямокутника – 65 кв. од. Де взялася зайва 1 кв. од.?

  Виконавши велику модель квадрата і умови розрізання, ми побачили, що точки  В, Е, F, D не лежать на одній прямій, а є вершинами дуже вузького паралелограма, площа якого і дорівнює 1 кв. од.

5.  Софізм Зенона, або Загадка руху

«Ахіллес і черепаха»

У V ст. до н. е. у Стародавній Греції жив уче­ний Зенон Елейський, який доводив те, чого бути не може. Його апорії не могли розгадати навіть наймудріші вчені. Одна з них — «Ахіллес і черепаха»

Ахіллес, що біжить в 10 раз швидше за черепаху, не зможе її наздогнати.

Припустимо, що Ахіллес бігає у 10 разів швидше, ніж черепаха, і знаходиться позаду неї на відстані 1 тисячі кроків.

За той час, за який Ахіллес пробіжить цю від­стань, черепаха в тому самому напрямку проповзе сто кроків. Коли Ахіллес пробіжить сто кроків, черепаха проповзе ще 10 кроків і т. д. Цей процес буде тривати до безкінечності, Ахіллес ніколи не на­здожене черепаху.

Уявіть собі кілометрову стежку, на початку якої стоїть Ахіллес, а посередині — черепаха.

Черепаха втікає від Ахіллеса. Неважко передба­чити, що Ахіллес наздожене черепаху. Але з іншого боку, можна довести, що він її не наздожене.

Справді, поки Ахіллес добіжить до середини стежки, черепаха за цей час зміститься вперед, поки Ахіллес досягне того самого місця, черепаха знову зміститься вперед і т. д. Таким чином, черепаха за­вжди буде попереду Ахіллеса і він її ніколи не зможе наздогнати.

Чому так відбувається?

( Річ у тому, що у Стародавній Греції мис­лили інакше, ніж мислять сучасні люди. Вони не допускали, що певні інтервали часу та шляху можна ділити нескінченною множиною поділок. Сьогодні ми кажемо, що рух — неперервний. За дуже маленькі інтервали часу тіло, що рухаєть­ся, проходить дуже маленькі відстані. При цьому інтервали часу і відстані можна ділити на менші частини, де з'являються нові закономірності. Тому задачі-апорії в ті часи роз'язати було не­можливо.)

6. Софізм Арістотеля

Усі кола мають однакову довжину.

При обертанні двох кіл з різними діаметрами OA₁ < ОА₂ кожне з них за один оберт ніби «спрям­ляється» на той самий відрізок ОО₁

7. «Софізм  навчання»

Cофізмом являється пісенька,  складена англійськими студентами:

The more you study, the more you know

The more you know, the more you forget

The more you forget, the less you know

The less you know, the less you forget

The less you forget, the more you know

So why study?

                                  

 

 

 

Чим більше вчишся, тим більше знаєш.                                                                          Чим більше знаєш, тим більше забуваєш.                                                                             Чим більше забуваєш, тим менше знаєш.                                                                            Чим менше знаєш, тим менше забуваєш.                                                                                                  Але чим менше забуваєш, тим більше  знаєш.                                                                                 Так для чого вчитися?

 Не філософія, а мрія ледарів!

8. «Повний стакан дорівнює порожньому»

Нехай є стакан на половину наповнений водою. Тоді можливе твердження, що на половину наповнений стакан дорівнює на половину повному. Збільшуючи обидві частини стакана вдвічі, одержуємо, що повний стакан дорівнює порожньому. Чи вірне дане твердження?

(Збільшення вдвічі неправомірне)

9. «Як стати мільйонером?”

Я знаю спосіб швидко збільшити свій капітал та стати мільйонером.

2 грн. = 200 коп.

Піднесемо ліву та праву частину рівності до квадрату:

( 2 грн .)2 = ( 200 коп.)2. Отримаємо 4 грн = 40000 коп. =400грн.     Де помилка?

 ( Порушені правила дій з іменованими числами:  всі дії, які виконуємо з величинами,необхідно виконувати  і з розмірностями.)

10. «Всі числа рівні»

Візьмемо два  різні числа  а  і b і запишемо для них відому нам тотожність

          а²-2аb+b²=b²-2аb+а²

           (а-b)²=(b-а)²

              а-b = b-а

              2а=2b

                а=b    Де помилка?

(Неправильно добутий корінь з квадрата числа )

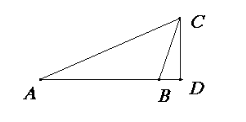
11. Квадрат будь-якої сторони у будь-якому трикутнику дорівнює сумі квадратів двох інших сторін цього трикутника.                                              Візьмемо довільний трикутник ABC і побудуємо ще прямокутний трикутник BCD. Тоді AC² = AD² + CD² (1) і BC² = CD² + BD², CD² = BC² - BD² (2). Підставимо значення з рівності (2) в рівність (1): AC² = AD² + BC² + BD² (3), або AC² - BC² = AD² - BD² (4). Але AD = AD + BD, тому AD² - BD² = AB². Підставивши в рівність (4) замість різниці AD² - BD² значення AB², яке їй дорівнює, матимемо,

 AC²-BC²=AB²або AC² = AB² + BC². 
Аналогічно Чернишевський "доводить", що BC² = AC² + AB², і закінчує лист словами: "... десь тут має приховуватися обман; відкривши його, ти зробиш велику послугу люблячому тебе брату Миколі Чернишевському".

 

   (Допущено логічну помилку "не випливає", яка полягає в порушенні закону достатньої підстави - в процесі доведення тези висуваються аргументи, самі по собі правильні, але такі , що з них не випливає висловлювання, істинність якого потрібно довести. З рівності AD = AB + BD випливає, що AB= = AD - BD, але зовсім не випливає, що AB² = AD² - BD². Мало б бути: AB² = AD² - 2AD*BD +BD².)

12. Софізм у вірші Степана Олійника

“Синок – математик”

До батьків, до Яблунова,

В рідну хату і садок

З політехніки зі Львова

          Гостювать прибув синок.

На обід прибув, до речі,

(Стіл накрили в акурат!)

Мати вийняла із печі

Двоє смажених курчат.

Син підняв до стелі руку:

Ось курчата ці: фактично

Двійко тут, як не бери.

А візьми математично,

Помудруй – і вийде три!

• Не мели дурницю синку!..-

(І, як видно, розізлив).

Той схопивсь: - Одну хвилинку!-

Щось помножив, поділив...

- Ось вам, - каже, - рівно троє.

Доказ точний і ясний! –

І промовив до старої

Сивий батько мовчазний:

Якщо так виходить в Петі,

Будуть двоє ці для нас,

Він хай їсть оте вже, третє!

Всім по одному якраз!

ІІ. Приклади парадоксів

1. Купа (парадокс Евбуліда із Мілета, 1V ст. До н.е.).

  Одне зерно купи не становить, додавши ще зернину, купи знову не матимемо. Як же дістати купу, додаючи кожного разу по одному зерну, з яких ні одне не становить купи?

  Проблема виникає при спробі знайти відповідь на питання, коли “не купа” переходить в “купу”. Тобто чи існує фіксована кількість елементів коли здійснюється названий перехід. У парадоксі, по суті, використано повну математичну індукцію, яку не можна застосовувати до  понять, обсяг яких не чітко визначено, а саме таким і є поняття “купи”. Крім того, в парадоксі ігнорується також об’єктивна закономірність будь-якого явища, в процесі перебігу якого кількісні зміни на певному етапі зумовлюють якісні зміни. При цьому нова якість (“купа”) зовсім не відгороджена від старої якості (“не купи”).

2. «Парадокс брехуна»

Людина промовляє «Я брешу». Бреше вона чи каже правду?

   З одного боку, він говорить неправду, тому що це стверджує. Але це означає, що він стверджує істину, а, отже, бреше.

Даний парадокс можна переформулювати й так. Припустимо, що на лицьовій стороні картки стоять слова: "На іншій стороні цієї картки написане щире висловлення" - і нічого більше. Ясно, що ці слова являють собою осмислене твердження. Перевернувши картку, ми знаходимо на її звороті слова: "На іншій стороні цієї картки написане помилкове висловлення" - і знову ж таки нічого більше. Припустимо, що твердження на лицьовій стороні - істинно. Тоді твердження на звороті має бути істинним і, виходить, затвердження на лицьовій стороні повинне бути помилковим. Але якщо твердження з лицьового боку хибно, тоді твердження на звороті також повинно бути помилковим і, отже, твердження на лицьовій стороні повинне бути істинним. Виходить, що дане твердження не може бути ні істинним, ні помилковим. Але це суперечить принципу виключеного третього.

 

3. Зорові парадокси

Зорові помилки та парадокси використав у своїх картинах відомий голландський художник  Мауріц Корнеліус Ешер (1898-1972)

  Своїми малюнками він глузує з певних особливостей нашого сприймання тривимірного світу, створюючи насправді вражаючі, просто дивовижні ефекти.

 

        

 

Неможливий водоспад.   Бельведер.     Підйом і спуск.

 

 

 

4. Парадокс з лініями

Накреслимо на прямокутному аркуші 10 вертикальних ліній однакової довжини. Проведемо діагональ. Розріжемо прямокутник по діагоналі і зсунемо нижню частину вниз, як показано на малюнку. Порахуємо кількість вертикальних ліній. Їх стало 9!

Отримані 9 ліній стали трохи довше, вони ніби увібрали в себе ту лінію, що зникла.

5.  Вкритий

   «Чи знаєш ти цього вкритого чоловіка?» «Ні». «Але цей вкритий чоловік — твій батько; отже, ти не знаєш свого батька».

   Коментар. М. І. Кондаков пояснює, що коли розглядати цей парадокс з погляду традиційної логіки, то він являє собою софізм, в якому є ніби двозначність дієслова «знати». Про вкриту людину не можна сказати, знаємо ми її чи не знаємо. Тому на питання потрібно відповідати так: «Оскільки ця людина вкрита, то мені невідомо, знаю я її чи не знаю». При такому підході софізм розв'язується легко.

   Якщо розглядати внутрішній зміст парадокса, то розв'язання його становить значно складнішу задачу. Тіль­ки німецький математик і логік

   Г. Фреге (1848-1925) зумів розв'язати цей парадокс за допомогою розроб­леної ним теорії опосередкованого використання імен предметів.

 

 

 

Висновки 

   Усе це був невеликий острівець галактики софістично-парадоксальних конструкцій думки, автори яких - невтомні шукачі істини або випадкові мадрівники в логічних лабірінтах. Вже багато віків математичні софізми  та парадокси бентежать людську думку, прокладають шлях до істини в хащах помилок, дають поштовх творчості, заманюють  несподіванками, вчать логічному мисленню, привчають до красоти бездоганних доведень.

     Процес пізнання людиною навколишнього світу можна порівняти з радісним торжеством, бо кожна розкрита таємниця зміцнює віру її в свої сили. Але на шляху переможної людської думки виникали величезні, здавалося б нездоланні, перешкоди – задачі, перед якими були безсилі найвитонченіші міркування. Вчені боляче переживали такі невдачі. Давньогрецький фі­лософ Діодор Кронос (пом. бл. 307 р. до н. е.), не розв'язавши однієї з найдавніших логічних загадок – парадоксу Евбуліда, помер від розпачу, а другий філософ Філет Косський, зазнавши такої самої невдачі, покінчив життя самогубством.

   Про математичні софізми та парадокси  можна говорити багато, як і про математику в цілому. Кожного дня зявляються нові парадокси, деякі з них залишаться в історії, а деякі існуватимуть всього один день.Софізми є суміш філософії і математики, яка допомагає  розвивати логіку і знаходити  помилку в міркуваннях.

 Зрозуміти софізм (розв’язати його і знайти помилку) виходить не відразу. Для цього потрібно мати навички і кмітливість. Розвинута логіка допоможе не тільки розв’язати математичні задачі, а й знадобиться в житті.

  Софістика- це ціла наука, а математичні софізми - це лише чистина однієї величезної течії.

    Досліджуючи софізми можна навчитися шукати помилки в міркуваннях інших,навчитися грамотно будувати свої міркування і логічні пояснення.

   Софізмом називається навмисне помилковий умовивід, який має видимість правильного. Який би не був софізм, він обов'язково містить одну або кілька замаскованих помилок.  Розбір софізмів, перш за все, розвиває логічне мислення, тобто прищеплює навички правильного мислення. Виявити помилку в софізм - це значить усвідомити її, а усвідомлення помилки попереджає від повторення її в інших математичних міркуваннях. Пам'ятайте, що важливо домогтися виразного розуміння помилок, інакше софізми будуть марні.

   Парадокс - це твердження яке, різко розходиться з загальноприйнятими, усталеними думками, заперечення того, що представляється "безумовно правильним".

   Парадокс у більш вузькому і більш сучасному значенні - це два протилежних твердження, для кожного з яких є представляються переконливими аргументи.

   Парадокси виникають в науці там, де теорія не описує процеси належним чином. Дозвіл таких парадоксальних явищ веде в свою чергу до виникнення нових теорій.

   Усунути парадокс з деякої  теорії - значить перебудувати її так, щоб парадоксальне твердження можливо було в ній довести.

  Рішення про відмову від якихось логічних засобів, що використовуються при виведенні парадоксального твердження, повинно бути пов'язане з загальними міркуваннями щодо природи логічного доказу та іншими логічними інтуїціями.

 Проблеми, пов'язані з парадоксами, відносяться до різних типів і зачіпають всі основні розділи логіки й математики.

 

 

Чим корисні софізми та парадокси для вивчення математики?

• Перш за все вони розвивають логічне мислення. Знайти помилку – значить не допустити її в майбутньому.
• По-друге, розгляд софізмів та парадоксів допомагає глибше засвоїти навчальний матеріал.
• По-третє, розгляд парадоксів та софізмів розвиває спостережливість, вдумливість, критичне ставлення до навчального матеріалу.
• Нарешті, це захоплююче заняття.

 

 

 

 

 

                  СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ

 1. А. Г. Конфорович “Математичні софізми і парадокси” К.: Радянська школа, 1983.

 2. Б. А. Кордемский “Математическая смекалка” М.: Государственное издательство технико-теоретической литературы (стор. 351 - 355).

 3. Математика после уроков. Пособие для учителей. М.: Просвещение, 1971 (стор. 151 - 153).

 4. Л. М. Лоповок “Збірник математичних задач логічного характеру” К.: Радянська школа, 1972 (стор. 80 - 84).

 5. М. Гарднер “Математические игры и развлечения” (глава 13).

 6. Толковый словарь математических терминов под редакцией В. А. Диткина М.: Просвещение 1965 (стор. 423).

 7. Энциклопедический словарь юного математика. М.: Педагогика, 1985 (стор. 276 - 278).

 8. Библер В.С. К философской логике парадокса [Текст] / В.С. Библер // Вопросы философии. – 1988. - №1. – (стор.28-42.)

 9. Винокур В.Г. Парадоксы древней науки [Электронный ресурс] / В.Г. Винокур. – http: // www.stq.ru/realiste/index. (21 чер.2008).

10. Войшвилло Е.К. Логика [Текст] : учеб. для студ. высш. учеб. заведений / Е.К. Войшвилло, М.Г. Дегтярев. – М.: Изд-во ВЛАДОСС-ПРЕСС, 2001. –( стр. 528 )

 11. Гладкий А.В. Введение в современную логику [Текст] / А.В. Гладкий. – М.: МЦНМО, 2001. – 200 с.

 12. Ивин А.А. Логика [Текст]: учебник / А.А. Ивин. – М.: Гардарики, 1999. –  (стор. 352 )

 13.  Ивин А.А. Теория аргументации [Текст]: учебное пособие / А.А. Ивин. – М.: Гардарики, 2000. –( стор 416)

 14. Новоселов М.М. Абстракция множества и парадокс Рассела [Текст] / М.М. Новоселов // Вопросы философии. – 2003. – №7. – (стор. 67-77)

 15. Ротенберг В. Парадоксальный сон, парадоксы природы и парадоксы науки [Электронный ресурс] / В.Ротенберг. – http: // flogiston.ru/self_behav7 (21 чер. 2008)

 16. Сухотин А.В. Парадоксы науки [Электронный ресурс] / А.В. Сухотин. – http: // bookz.ru/authors/anatolii-suhotin/suhota01. (21 чер. 2008).

 17. Чунина А. Парадоксы в науке [Электронный ресурс] / А. Чунина. – http: // portfolio.1september.ru. (21 чер. 2008).

 18. Шарков В.Ф. Наука для Эволюции или Парадоксы развития Науки [Электронный ресурс] / В.Ф. Шарков. – http: // www.cosmoenergy.ru/science1_rus. (21 апр.2008).

 19. Щипкова А.В. О фундаментальной гносеологической роли парадоксов [Электронный ресурс] / А.В. Щипкова. – http: // www.philosophy.ru/phas/library/phnauk4/schip. (21 апр. 2008