Розроблено та проведено вчителем математики

ЗОШ № 7 ім. В. В. Бражевського м. Житомира

Сергієм Олександровичем Сафонюком

                   

УРОК № 1

ТЕМА:               Кути. Вимірювання кутів. Бісектриса кута.

ТИП УРОКУ: Практична лекція

МЕТА УРОКУ: Розширити поняття про кути, їх вимірювання та побудову,   познайомитись  із новими поняттями та практичним застосуванням нових знань

.

 

ПЛАН УРОКУ

1.     Активізувати знання, вміння  та навички учнів.

2.     Поставити проблемне питання.

3.     Пояснення нової теми.

4.     Отримання учнями домашнього завдання.

5.     Підведення підсумків уроку.

 

ХІД УРОКУ

1.Математичний диктант ( так/ні )

1)         геометрія – це властивість фігур                                                    ні

2)         точка – найкоротша геометрична фігура                                      так

3)         в 7-му класі вивчають стереометрію                                             ні

4)         пряма – це лінія, яка не має ні початку, ні кінця                          ні

5)         відрізок – це частина прямої, який має початок і кінець             так

6)         два промені, які мають спільний початок, називаються

доповняльними                                                                                ні

Практичні питання (вибери правильну відповідь)

7)         що дерев’яна рейка не рухалась досить прибити її

А Б                                     В

            одним цвяхом           двома цвяхами більше двох цвяхів                  Б

8)         щоб з’ясувати чи куплена вами лінійка є якісною можна

А Б                                   В

       виміряти ширину        порівняти з іншою поставити ребром                       клітинок зошита лінійкою                     на рівну поверхню          В

9)         діаметр голки можна більш-менш точно виміряти за допомогою

    А Б                                   В

штангенциркуля       швейного метра мікрометра                    В 

10)     прямі a і b мають спільну точку М і це записують так

А Б                                  В  

            М є a, М є b                a = bМ a I b = М                         А

11)     дві точки А і В належать прямій а і це записують так

                                    А Б                                  В  

                   А, В є а                а  є А, В                         {A, B}  а                      В

 

 

 

 

12)     що, на вашу думку, означає вислів “ направити дитину                    в куток”

               А Б                                 В

        покарати її               вимагати відповісти            шукати подарунок                                                   на незрозуміле їй                під новорічною

питання                         ялинкою 

Відповідь на останнє питання ми надамо нижче.

Математичний диктант перевіряється за допомогою учнівської взаємоперевірки.

2.                  Відповідаючи на 12-питання диктанту, ви, можливо, не задумувались над тим: “А що таке кут? Чому на уроках геометрії ми повинні розглядати це?”  Познайомившись з поняттям “кут”, ми з вами  зможемо впевнитись, що відповіддю на останнє питання може бути  будь-який варіант. Адже, декого “ставили в куток” за якусь провину; комусь ставили питання, яке ви не розуміли або на яке не знали відповідь ( в народі з цього приводу кажуть “загнати в глухий кут”; дехто знаходив подарунки під ялинкою, яка стояла в кутку кімнати.

   Так що ж таке кут? (Вислухати думки учнів).

3.                  Тож сьогодні на уроці ми познайомимось з “кутами”, з тим як і за допомогою чого вимірюються кути та що таке бісектриса кута. 

3.1. Означення: кутом називається частина площини, яка обмежена двома променями зі спільним початком. Це геометрична фігура.  

   

 

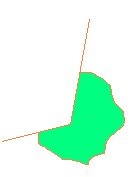
Для простоти розв’язування задач та на практиці кутом вважають фігуру, яка утворена двома променями зі спільним початком.

Кути позначають так:

1) 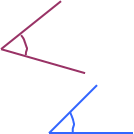                                                                                                                         А АВС або СВА, де В – вершина кута,                                                         ВА і ВС – сторони кута.

                                                                                                     Зауваження: вершина кута у запису повинна 

                В                                             бути посередині.

                                 С

2)                                                                                                                          Читають – кут _ (кут альфа). В підручнику є

                         _                           грецький алфавіт.

 

 

 

 

3) 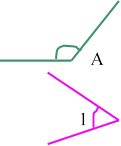                                                                                                                         А (кут А)

 

 

 

4)                                                                                                                          _ 1 (кут один)    

 

 

3.2  Які ж бувають кути та чим вони відрізняються?

          ( вислухати думки учнів)

   Щоб з’ясувати це нам допоможе годинник

   1)  2)     3) 4)

 

_

 

 

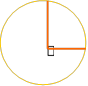
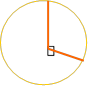
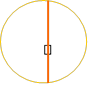
                                     14⁰⁰                   15⁰⁰ 16⁰⁰                       18⁰⁰

        5)

                                       2400

Різні кути, ну й що?

Пов’яжемо їх з вашою навчальною діяльністю. Отже:

1)    14⁰⁰ – гостро хочеться їсти та піти додому (гострий кут);

2)    уроки закінчилися – прямісінько додому (прямий кут);

3)    сиджу, роблю уроки і вже втомився (“голова не варить“ або на молодіжному сленгу – “туплю”) (тупий кут)

4)    все зроблено, піду на вулицю (сяду за комп’ютер, пограюсь з братиком (сестричкою),допоможу по хазяйству і т.д. (на вибір), що іншими словами іноді кажуть: “розгорнути бурхливу діяльність” (розгорнутий кут);

5)    вже сили і моя активність на “нулі” (нульовий кут).

3.3 Що роблять з кутами? Їх вимірюють Для цього існують різні інструменти, але в школі використовують транспортир.

Кути ми будемо вимірювати в градусах, тобто знаходити їх градусну міру.  В 7-му класі вивчають кути від 0⁰ до 180⁰ (в підручнику читають означення видів кутів; коментар вчителя).

Весела хвилинка. В народі кажуть: “Чим більше в середині градусів, тим тупіше”. Чому?

3.4. Працюємо разом за принципом “вмію сам – допоможу іншому”. Завдання: побудувати кути: АВС=40⁰, _MNP=120⁰.

 

 

Постає проблема: а як поділити кут навпіл? (Вислухати думки учнів.)  А якщо кут дорівнює 47⁰? 

Спробуємо вирішити цю проблему разом. Накреслимо на аркуші паперу кут (бажано фломастером або маркером) і згорнути його так, щоб сторони кута співпадали.

Питання: що для кута є лінія згину? (Означення читаємо в підручнику.) За допомогою рисунків закріпимо поняття “бісектриса”.

На якому з рисунків вірно зображено бісектрису? Чому?

       А Б                           В                                   Г

                                                

 

 

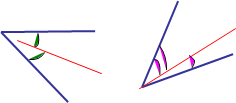
А як за рисунком взнати, що кути рівні?

В геометрії це показують так: рівні кути позначають однаковими дужками.

 

                                                 

 

 

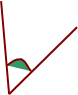
4.       Домашнє завдання. 

1.     Почати підготовку до захисту своїх знань, вмінь та навичок, отриманих при вивчені даної теми та двох наступних тем.. Причому, висвітити питання: “Як на практиці (в побуті, техніці, інших галузях науки) вимірюють кути і в яких одиницях?”

2.     Розв’язувати з поясненням (можна усно) наступні практичні вправи: № 39, №42, №43 з параграфа 3.

3.     Вивчити зазначені в параграфі означення та подумати над питанням: “Що таке повний кут?”

5.       Підведемо підсумки уроку.

     На уроці ви ознайомились з поняттями: “кут”, “бісектриса”, “градусна міра”, розглянули види кутів,  методи їх побудови та вимірювання.

     Хочу звернути увагу на практичне застосування отриманих знань. 

 

           

 

 

 

 

 

УРОК № 2

 

ТЕМА:                     Кути. Вимірювання кутів. Бісектриса кута

ТИП УРОКУ:    Урок узагальнення знань, вмінь та навичок учнів.

 МЕТА УРОКУ:  Розв’язування задач: на побудову кутів, знаходження

                                 градусних мір кутів та їх частин, практичного застосування                                   набутих знань, вмінь та навичок.

 

 

ПЛАН УРОКУ

1.     Перевірка домашнього завдання.

2.     Розв’язування задач з підручника.

3.     Розв’язування практичних задач.

4.     Самостійна робота.

5.     Завдання додому.

6.     Підведення підсумків уроку.

ХІД УРОКУ

1.1 Теоретичне опитування учнів 1) Що таке кут?

2)    Які існують кути?

3)    Що таке бісектриса кута?

      1.2  Опрацьовування домашніх задач.

                             № 39   на 45⁰, № 42   накладанням або порівнянням

                             № 43   21 год 39 хв, 14 год 30 хв, 9 год 30 хв, 2 год 30 хв.

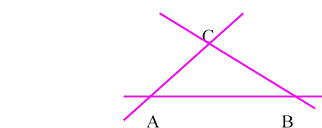
      2. Розв’язування задач: № 8 (усно), № 12 (усно), № 15, № 18 (1,2), № 21 (1) № 8 Скільки зображено кутів на рисунку:

1)   з вершиною А, що не є розгорнутими;              4 кути

2)   з вершиною В, що є розгорнутими;                   2 кути    3) з вершиною С ?                                                    6 кутів

             № 12 Порівняйте градусні міри заданих кутів.

1)    _А = 40⁰, _В = 39⁰59^/, _С = 40⁰1^/                  _В < _А < _С

2)    _А = 50^/, _В = 50⁰, _С = 500^/                         _А < _С < _В

3)    _А = 0,5⁰, _В = 30^/, _С = 3⁰                           _А = _В < _С № 15 Промінь, що  проходить між сторонами кута  , розбиває його на два кути - _ і  . За даними, наведеними в таблиці, знайдіть градусні міри даних кутів.

 

 

	900				n0		1000				1200				n0		1800
	2n0		600		500						n0		400		n0/3			600
	n0		300		0,5 n0			500			n0 + 400		800		1200

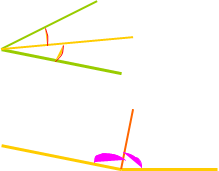
          № 18        А                          Дано: АОВ, ОС - бісектриса

1)                                                                                                          1) АОС = 36⁰

2)                                                                                                          АОВ = 174⁰                 

       О                         С                  Знайти 1)  АОВ, 2) ВОС

                В                        Розв’язування

      2) 1) ОС – бісектриса  АОВ = 2АОС = 72⁰

                С                   2) ОС – бісектриса  ВОС = 0,5АОВ = 87⁰ 

       А

           

                                                 О В

Відповідь: 1) 72⁰, 2) 87⁰.

Примітка: пояснити учням, що можна кути зображати схематично, не дотримуючись даних умови задачі Але, якщо кут гострий – зобрази його гострим, якщо тупий – тупим.

           №21       А                             Дано: АОВ = 62⁰

С                           ВОС = АОС + 20⁰ Знайти: ВОС

О                                                Розв’язування

Примітка: зв’язок між алгеброю та                                  В геометрією.                                                        Нехай  АОС = х⁰, тоді   ВОС = (х + 20)⁰.

Складемо рівняння: х + х + 20 = 62,

2х + 20 = 62,

2х = 42, х = 21.

      Тобто АОС = 21⁰, тоді ВОС = 21⁰ + 20⁰ = 41⁰.

      Відповідь: 41⁰.                 

3.   Проблема: як без допомоги транспортира побудувати кути: 30⁰, 60⁰, 90⁰?

                              30⁰ 60⁰                           90⁰                  90⁰

4.   Самостійна робота: провести бісектриси кутів: 20⁰, 78⁰, 126⁰, 150⁰.

5.   Повторити п. 3. Розв’язувати № 23, 19, 31 (практична задача).

6.   На уроці вчилися розв’язувати задачі, правильно оформлювати           розв’язання, з’ясували, як клітинки допомагають будувати кути та оцінили          свої знання при виконання самостійної роботи

 

 

Урок № 3

ТЕМА УРОКУ     СУМІЖНІ ТА ВЕРТИКАЛЬНІ КУТИ

ТИП УРОКУ         ЛЕКЦІЯ

МЕТА УРОКУ        Відкрити для себе нові поняття, вчитись шукати методи для                           доведення певних міркувань та тверджень, спробувати знайти практичне застосування почутого на уроці.                                 ПЛАН УРОКУ

I.                   Актуалізація знань, вмінь та навичок учнів.

II.                Давайте посперечаємось.

III.             Пояснення нової теми.

IV.            Знаходження практичного використання даної теми. V.   Домашнє завдання.

                        VI.    Підведення підсумків уроку.

                            ХІД УРОКУ

I. Математичний диктант

     Перший         блок –        теоретичні питання      (потрібно    вставити     слово   або словосполучення, щоб вираз був вірним). 

1) довжина будь-якого відрізка;                                            /більша за нуль/ 2) промінь, який виходить з вершини кута і ділить            /бісектрисою/ його навпіл, називається;      

3)          два промені, які мають спільний початок і /доповняльними/     утворюють пряму, називаються;

4)          якщо дві прямі мають спільну точку, то вони; /перетинаються/ 5) якщо частина прямої має початок і не має кінця, /променем/     то вона називається;

6) наука про властивості геометричних фігур – це.            /геометрія/      Другий блок – практичні питання (вибрати один з варіантів відповіді). 7) для паперового літака лінія згину є: (показати, про що йде мова)

     А: противагою    Б: неважливо чим      В: бісектрисою кута між крилами

8)   чи можна за допомогою трьох мотузок довжиною 8м, 4м, 3м виміряти довжину 10м?

      А:  так                 Б: ні                             В: мало даних

9)   стрілки годинника можуть утворювати кут 180^o

      А: один раз         Б: два рази В: більше двох разів       Третій блок – усні вправи. 10) відрізок 8см поділили на 5 частин і виміряли  довжину 2 частин.

 Яка довжина виміряної частини?                                                                /3,2см/

 11) <А=40^o, <B на 30^o більший. Чому дорівнює 2B3A? /20⁰/

12)*AOB 68^o,COA 34^o,тодіCOB_? /102⁰ або 34⁰/

    (Перевірка диктанту проводиться в парах)

  II. Ми живемо з вами в досить складному, але цікавому світі. Я пропоную вам декілька тверджень:

1)    кожна дитина має право на освіту;

2)    всі хлопці вміють грати у футбол;

3)    якщо ви не вивчили вірш, то сьогодні отримаєте низький бал; 4) наркотики – це смерть.

Давайте проаналізуємо, які з тверджень потребують доведення, а які ні.

( Учні висловлюють свої думки).

    III. Отже, ми прийшли до висновку, що істинність деяких тверджень встановлюються міркуванням, а інші твердження приймаємо такими, як вони є.         В геометрії певні твердження поділяються на дві категорії (учні знаходять в  підручнику означення теореми та аксіоми та аналізують вислови з п.II).

        Сьогодні на уроці ми будемо вчитись доводити де-яки твердження, щоб потім їх можна було б використовувати при розв’язуванні задач.

        Як це робити ми розглянемо при вивченні нової теми: “Суміжні та вертикальні кути”.

 III.1 Побудуємо кут   ABC.                  А

B                                                          A

                                                              C

і продовжимо сторону BC ліворуч.                            D          В               C

Отримали два кути: <ABD і <ABC, у яких сторона BA – спільна , а BD і BC –     доповняльні  промені. Такі кути називаються суміжними. (Означення читаємо в підручнику).

 Питання: якщо виміряти <ABD і <ABC, то чому буде дорівнювати їх сума?

ТЕОРЕМА (читаємо в підручнику)

A                             Дано: <ABC і <ABD – суміжні                                                               Довести: <ABC + <ADC = 180^o                                                                                   Доведення.

      D           B              C         BD і BC – доповняльні промені, тому <DBC=180^o . BA ділить <DBC на два кути: <ABD і <ABC, отже                                                   <ABD + <ABC =180^o . Теорема доведена.  Чи досить знати градусну міру одного з суміжних кутів, щоб знайти другий кут?

( Декілька усних вправ).

  Слово “суміжні” зустрічається і в побуті:

-         суміжні кімнати – кімнати, що мають спільну стіну;

-         суміжні підприємства – підприємства, що виготовляють взаємно необхідну продукцію і т.д.  Принцип “по гарячих слідах”.

       120 ^o ?          ?        24^o                

 

 

   Питання: 1) на якому з рисунків зображено суміжні кути?

               2) чи можемо ми визначити градусну міру невідомого кута? Чому? Як?

 

 

 

 

 

 

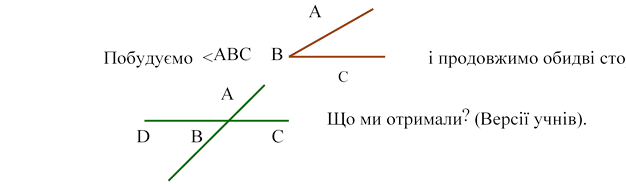
                                    F

А як назвати кути ABC і DBF? Щоб прийти до означення таких кутів приведу один приклад. Майже всі ви бачили, як будівельники зводять стіни, при цьому використовуючи деякий предмет на мотузці. Він називається висок (від слова “прямовисний”). А це слово походить від слова “verticalis” (вертикальний). А з

уроків географії та фізики вам відомо, що                           - горизонтальна лінія, а           

 

-   -  вертикальна. І ще одне. Ви бачили пісковий годинник? Як падає пісок? А чи  не нагадує він вам за своєю формою вертикальні кути?

Означення читаємо в підручнику. А яка властивість вертикальних кутів? ТЕОРЕМА (читаємо в підручнику).

 

                                          D                                        Дано: <ABF і <CBD – вертикальні 

 Довести: <ABF = <CBD

 Доведення

 <ABF + <FBD =180^o (суміжні)

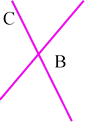        A                  F <CBD + FBD =180^o (суміжні), а тому <ABF=<CBD.

                                                                       Терему доведено.

“По гарячим слідам”.

1)   знайти невідомі кути  

 

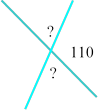 o

  

 

2)   на якому (яких) рисунках зображено вертикальні кути?

 

                                            а)                                             б)                                                в)

IV.     Що з’ясувати, чи дійсно ваша кімната має прямокутну підлогу, можна

зробити так. 

 

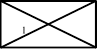                                                                            2

 

 

Якщо <1_ <2, то будівельники “зробили халтуру”.

При подальшому вивченні геометрії ми знайдемо ще інші шляхи для відповіді на дане питання.

V.        Вчити п. 4,5. Розв’язувати №8,9(п.4);№7,35(практичне завдання)(п.5)      Завдання групам: до свого захисту по темі “Кути” включити цікаві факти про суміжні та вертикальні кути.

VII. При підведенні підсумків уроку дамо відповіді на питання:

-         що дізнались нового;

-         чи цікаво було;

-         чи можна десь використати нові знання?

P.S. Фізкультхвилинка після “суміжних кутів”.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

           

 

 

 

 

 

 

 

 

 

 

 

 

 

УРОК № 4

ТЕМА                       СУМІЖНІ ТА ВЕРТИКАЛЬНІ КУТИ

                Тип уроку            Розв’язування задач

 Мета уроку        Закріпити за допомогою розв’язування задач знання, вміння                     та навички, отримані при вивчення даної теми; продовжити          вдосконалювати вміння працювати в групах.

 

                ПЛАН УРОКУ

I.   Актуалізація знань учнів. II.      Розв’язування задач.

III.             Отримання домашнього завдання.

IV.            Підведення підсумків уроку.

                                                       ХІД УРОКУ

I.                   Перевірка домашнього завдання. Усне опитування теоретичного матеріалу.

II.                Розв’язування задач в групах.

    № 10(1) п.4, № 13(2) п.5, №21(2) п.4, № 24(1) п.5, № 23(3) п.4, № 28* п.5,     № 30*(2).

P.S. В зв’язку з великою кількістю задач, пояснення розв’язку задач при відповіді можна робити усно.

№ 10(2) Дано: <1 і <2 – суміжні           

                                                                        <2-<1=30^o

                                                                  Знайти: <1,<2                                                                      

 

                                                                  Розв’язування

                                                          Нехай <1=x, тоді <2=30^o -x. <1+<2=180^o (суміжні).

 Складемо рівняння: x+30+x=180 _ x=75.  Відповідь: 75^o ,105^o .

                №13(2)                                                    Дано: <1-<2=56^o

 Знайти:<1,<2,<3,<4.  Розв’язання

 <1+<2=180^o (суміжні). Нехай <2=x, тоді <1=x+56.  Складемо рівняння: x+56+x=180^o _ x=62.

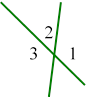                                            4        <2=62^o ,<1=118^o . Отже, <3=<1=118^o , <4=<2=62^o                

                (вертикальні).

Відповідь: <3=<1=118^o , <4=<2=62^o .

                № 21(2)                                   Дано: <1 і <2 – суміжні           

                                                                                                                 <1 : <2= 1:11           

 Знайти: <1,<2.  

 

                Розв’язання

                                                         Нехай x – коефіцієнт пропорційності, тоді <1=x, 

                                     <2=11x. Складемо рівняння: x+11x= 180 (суміжні); x=15.

                                          Відповідь: 15^o ,165^o .

 

№24(1)    Дано: aIb     Розв’язання:

          <1 + <3 = 320^o         Так як <1 + <3 = 320^o , то <1 і <3 –                                                               несуміжні,

                 Знайти: <1,<2,<3,<4. а отже – вони вертикальні, тобто 

<1=<3=160^o

 Тоді на інші два кути припадає 40^o , а це  

 означає, що <2=<4=20^o , бо вони теж         вертикальні.

                                                                            Відповідь: <1=<3=160^o ,<2=<4=20 ^o .

№ 23(3)

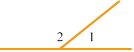 Дано: <1=0,2<2 Знайти:<1,<2.

                                                                Розв’язування

                                                           Нехай <2=x, тоді <1=0,2x. <1+<2=180^o (суміжні).

 Складемо рівняння: 0,2x + x =180 _ x=150  Відповідь: 150 ^o , 30 ^o .

№ 28*(1) 

                Дано: <1 і <3 - вертикальні                Розв’язування

                                       (<1+<3)M9 Так як <1 і <3 – вертикальні, то

          55^o_<1+<3_70^o <1 = <3 і <1 і 55^o_<1+<3_70^o , а    Знайти:<1,<3. серед чисел від 55 до 70 є 

тільки одне число, яке кратне 9 – це 63.

                                                                                             Відповідь: <1 = <3=31,5^o

№ 30(2) 

                                                                            Дано: _ і _ - суміжні

            _{ }                                            120^o _130^o Знайти: ?  _ _ ?     

                                                                         Розв’язування

 

                                                         +  = 180o (суміжні)180oo 120oo  60oo, 

180 130  50

                                                    _ 50^o _ _ 60^o .

 

                                                            Відповідь: 50^o _ _ 60^o .

III.             На наступний урок принести підручний матеріал, за допомогою якого можна на місцевості побудувати суміжні та вертикальні кути. Підготувати в чорновому варіанті захист групи по темі “Кути”.

IV.            Сьогодні вчилися розв’язувати задачі, працювати в групах, оцінювати свою роботу та роботу інших. А що ви думаєте з цього приводу? (Вислухати думки учнів).

P.S. Дозволити проводити фізкультрозминку в кожній групі по мірі необхідності.     

 

 

 

УРОК № 5

Урок -  практикум з геометрії в 7-му класі

 

 

 

 

 

Тема уроку        Суміжні  і вертикальні кути

Мета уроку 1.	Узагальнити відомості про кути
2.	За допомогою практичних завдань перевірити знання , вміння та навички учнів по даній темі.
Обладнання  1.	Мультемедійний пристрій
2.	Учнівські електронні носії інформації
3.	Мотузки
4.	Учбовий транспортир
5.	Цифровий фотоапарат.
План уроку І.	Перевірка домашнього завдання

        ІІ. Виконання практичної роботи        ІІІ. Обговорення в групах ходу виконання практикуму

                                          ІV. Підведення підсумків уроку

                                           V. Отримання учнями домашнього завдання

Хід уроку

 

       Домашнє завдання було розподілено між групами учнів. Воно полягало в тому, щоб за допомогою мультемедійної презентації узагальнити  відомості про кути.

 

1 група.    

 

Завдання: «Кут, його позначення, одиниці
вимірювання кутів»		Презентація
Захист групи
частина ма променями з -му класі ми 0
	М
	α
	1,      2,  3,        4
	в градусах : 370 в радіанах: 2рад=114036І в градах: 1град ≈ 0,90 в румбах: 3 румби = 33,870

Кутом називається площини, яка розташована між дво

спільним початком. Це може бути так, але в 7 розглядаємо кути до 180 Кути можуть позначатися:

а) трьома літерами

 

б) однією літерою (вершина)

 

 

в) грецькою літерою

г) числом, якщо на рисунку багато кутів. Кути вимірюються:

 

а) в школі;

б) в промисловості;

в) в метрології;

г) в мореплавстві

 

 

 

 

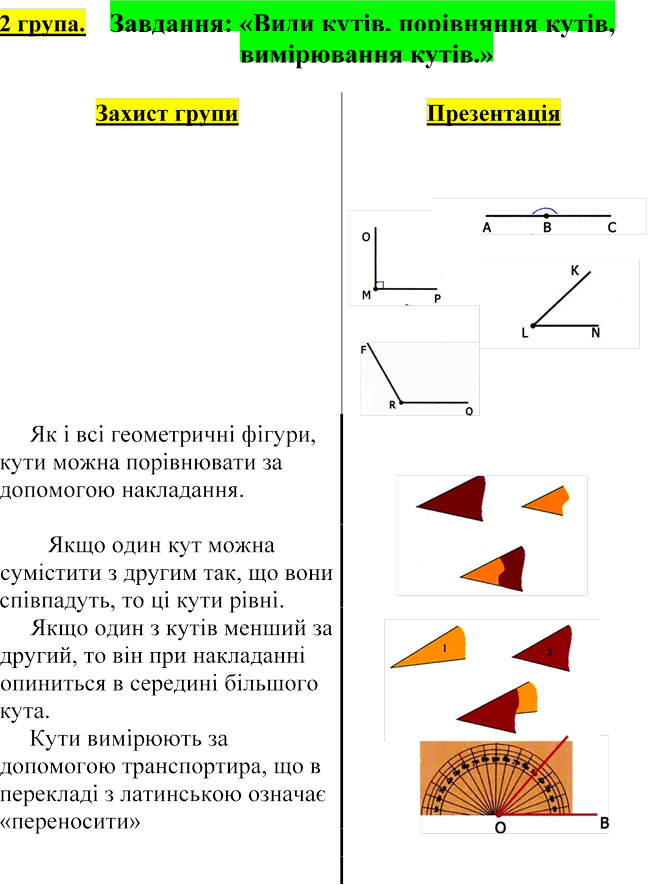Існують такі кути:

•      Розгорнутий кут;

•      Прямий кут;

•      Гострий кут;

•      Тупий кут

 

 

 

 

 

 

 

3 група.    Завдання: «Кути навколо нас»

 

Захист групи

 

     В повсякденному житті поняття «кут» та і самі кути зустрічаються нам доволі часто.      Дітей часто ставлять у «куток».

Існує вислів: «Залежить від того, під яким кутом подивитись»

  Уяву про кути нам дає звичайний годинник:

-   о 6-тій  годині стрілки утворюють розгорнутий кут;

-   о 3-тій годині – прямий кут;

-   о 5-тій годині – тупий кут;

-   о 2-гій годині – гострий кут.

 

 

     А ще є речі навколо нас, які дають уяву про:                      

 

       суміжні кути (двірники автомобіля)

 

                       і

   вертикальні кути

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

4 група.    Завдання: «Це цікаво»

 

Захист групи

Цікаві факти

  Знак для позначення кута ввів в 17-му столітті  французький математик

П.Ерагон.                                  

Транспортир спочатку служив для побудови кута рівного даному.

Ще до 18-го століття для виміру  кутів використовували давній інструмент астролябію (капкан для зірок)

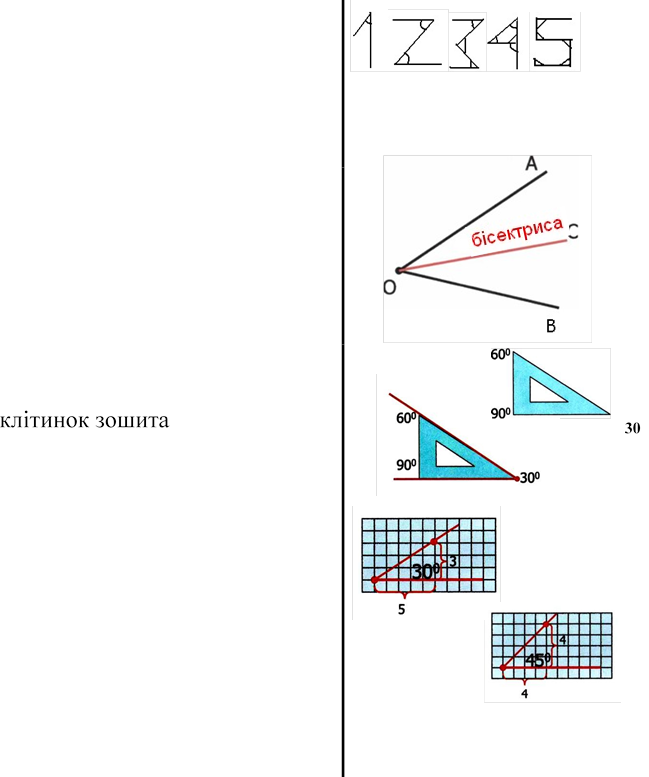Зараз використовують теодоліт Цікаво , що між кутами і деякими числами існує зв'язок 

А ось як можна отримати бісектрису кута:

Якщо взяти кут, вирізаний з листка бумаги, то його бісектрису легко знайти перегибом. Кут треба скласти так, щоб його сторони співпадоли. Лінія перегибу і буде бісектрисою цього кута.   

Так можна побудувати деякі кути за допомогою косинців та ІІ.практична робота.

Завдання 1. За допомогою трьох (!) мотузок утворити суміжні кути.

 

Під час виконання цього завдання учні дадуть відповідь на 2 питання: 

1.   Чому вони вважають, що утворені кути є суміжними ?

2.   Яка властивість суміжних кутів ?

За відповідь на ці питання група отримає оцінку, яка залежитиме від формулювання та правильності відповіді.

(Один із варіантів відповіді:

1)   вони суміжні, бо одна сторона (мотузка) є спільною, а інші дві є доповняльними півпрямими (утворюють  пряму);

2)   сума цих (суміжних ) кутів дорівнює 180⁰

 

 

 

 

 

 

Завдання 2. За допомогою 4-х (!) мотузок утворити    вертикальні кути.

 

     Під час виконання цього завдання учні дають відповідь на наступні питання:

1.   Які з утворених кутів є вертикальними? Чому ?

2.   Скільки  серед даних кутів вертикальних і скільки суміжних?

3.   Яка властивість вертикальних кутів?

 

        За відповіді на ці питання група теж отримає оцінку.

  Один з варіантів відповіді: 

1)   учні показують вертикальні кути. Вони вертикальні, бо сторони одного кута є доповняльними півпрямими для сторін другого кута (сторони цих кутів утворюють дві прямі, що перетинаються у точці, яка є спільною вершиною).

2)   дві пари вертикальних і чотири пари суміжних кутів.

3)   Вертикальні кути рівні.

 

 

 

    Під час демонстрації кутів доцільно використовувати асоціацію з життєвими простими ситуаціями  Наприклад:

-         суміжні кути – сусіди, межа у полі (учні стають пліч- о – пліч в суміжні кути і по сусідські, по дружньому обіймаються);

-         вертикальні кути – рівні права (учні стають обличчям один до одного у вертикальні кути і тиснуть один одному руки як рівноправні члени суспільства).

 

 

Завдання 3 (проблемне) Виміряти градусну міру кута при наявності певної перешкоди.

  Учні разом з вчителем виконують це завдання .

Вчитель  ставить 3 проблеми:

-         проблема 1: перешкода в одному з суміжних кутів.  Розв’язання проблеми: виміряти градусну міру суміжного кута  і відняти її від

180⁰  (учні при цьому використовують властивість суміжних кутів.

-         проблема 2: перешкода в одному з вертикальних кутів.

    Розв’язання проблеми: виміряти градусну міру вертикального йому кута. (учні використовують властивість вертикальних кутів.)

         

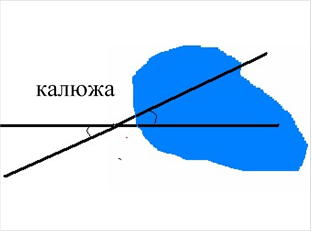-         проблема 3: перешкода у куті.    

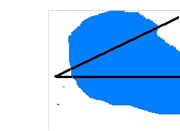калюжа

Розв’язання проблеми: добудувати або суміжний, або вертикальний кут і далі за допомогою транспортиру вимірюємо кут (учні використовують означення та властивості суміжних або вертикальних кутів).

ІІІ Учні в групах обговорюють хід практичної роботи і                 складають план виконання роботи.

   Орієнтований план

1.   Суміжні кути

2.   Вертикальні кути

3.   Кути з перешкодою

4.   Висновки

 

ІV  На уроці були узагальнені відомості про різноманітні кути, їх властивості і побудову, де норма в побуті зустріти різні види кутів.

   На практичному занятті повторили означення та властивості суміжних і вертикальних кутів. Навчитися використовувати набуті знання при вирішенні проблем з вимірюванням градусної міри кута.

 

V Домашнє завдання. Опрацювати в групах та описати хід практичної роботи. Зробити висновки.

 

P.S. Під час роботи кожна група отримала оціночні таблиці, які заповнювались під час уроку.

Завдання	Оцінка вчителя	Самооцінка групи	Оцінка інших груп	Середня оцінка групи
1.      Мультимедіа 2.      Суміжні кути 3.      Вертикальні кути 4.      Перешкода 5.      Домашнє завдання
Середній бал