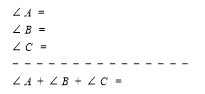Розробка уроку на тему "Сума кутів трикутника"

7 клас

Геометрія

Тема уроку. Сума кутів трикутника

Мета уроку: ознайомити учнів з теоремою про  суму кутів

трикутника, формувати навички знаходження різних способів доведення цієї теореми та навички застосування її до розв’язування задач, показати застосування здобутих знань у практичній діяльності; розвивати логічне мислення, вміння аналізувати факти, робити висновки, виховувати культуру спілкування, доброзичливість.

Формувати в учнів різні групи компетенцій:

• Соціальні – бути готовим до громадського життя, уміння

                 відстоювати свою точку зору, усвідомлення

                 власного внеску в спільну роботу, здатність

                 рефлексії;

• Полікультурні – опанувати засади культурного спілкування

                           в ході обговорення проблеми, розви-

                           вати вміння вести групову бесіду;

• Інформаційні – уміння використовувати різноманітну

                         інформацію, розширення кругозору,

                          гнучкість застосування знань;

• Самоосвітні й самонавчання – розвивати  ініціативність, готовність навчатися, пам'ять, увагу, естетичне сприйняття, пізнавальні здібності, самоконтроль за власною діяльністю.

Тип уроку: урок вивчення нового матеріалу.

Обладнання: портрет Евкліда, виставка малюнків

                             « Трикутна фантазія учнів 7 класу»,

                             кольоровий папір, ножиці, олівці, лінійки,

                             листок самооцінки.                  

Підручник:  Апостолова Г.В. Геометрія: підручник для 7  класу загальноосвіт. навч. закл.-К.:  «Генеза»,    2015.

Епіграф уроку.

      Найвищий прояв духу – це розум.

        Найвищий прояв розуму – геометрія.

        Клітина геометрії – трикутник.                      (1)

        Він такий же невичерпний, як Всесвіт.

                          Давньогрецький мудрець.

… Как для смертных истина ясна,

Что в треугольник двум тупым не влиться.         (2)

                               Данте А. (1265 – 1321)

Девіз уроку.

Найкращий спосіб вивчення чого – набудь – це  самостійний пошук.

                 Попередня робота.

1.  Випереджаюче завдання ( було задано на домашнє завдання): Знайти суму кутів трикутника

Обладнання: лінійка, олівець, транспортир.

Алгоритм виконання:

а ) накреслити прямокутний, тупокутний,  гострокутний трикутники;

б ) виміряти кути для кожного трикутника;

в ) знайти суму кутів кожного трикутника S1, S2, S3.

г) округлити кожен з результатів до десятків: S1≈ S2≈S3≈…

д) висновок.

2. Намалювати малюнок із трикутників

3. Скласти сенкан про трикутник

Хід уроку

I. Організаційно – психологічний етап.

     Щоб бути успішним у житті, треба довести, що ти щось умієш робити. На сьогоднішньому уроці ви матимете можливість, по мірі своїх знань та умінь, виконати різні завдання і показати свою наполегливість у досягненні поставленої мети.

II. Перевірка домашнього завдання.

1.  Використовуючи дані із домашньої роботи, заповнити    таблицю

Графічне зображення	Назва трикутника залежно від кутів	Градусна міра кутів трикутника
	Гострокутний
	Тупокутний

 

( один учень заповнює біля дошки)

 

2. Зачитати складений сенкан про трикутник

       НАПРИКЛАД:

1. Трикутник.

Цікавий, найрізноманітніший.                                                   Складається, застосовується, зображується.                                   Важлива властивість жорсткість.                                                               Фігура.

2. Трикутник.

Захоплюючий, важливий.                                                   Будується, застосовується, складається.                                       Їх світ різноманітний.                                                     Геометрична фігура.

 

3. Назвати зображені фігури

 

 

 

 

 

 

4. Графічна вправа на перевірку вивченого

матеріалу « ТАК – НІ»

( відповідь учні дають значками: ТАК – "^"

                                                        НІ - "-"                 )

 

• Геометрія – це наука про властивості геометричних фігур ( ТАК)
• Кут – геометрична фігура, яка складається з точки і двох променів, що виходять з цієї точки.( ТАК)
• Прямокутний трикутник має кут 90 ( ТАК)
• Залежно від кутів розрізняють такі види прямокутників: рівносторонній, рівнобедрений,  різносторонній ( НІ)
• Трикутником називають фігуру, яка складається з трьох точок, що не лежать на одній прямій і трьох відрізків, які сполучають ці точки.( ТАК)
• У рівнобедреному трикутнику всі сторони рівні( НІ)

 

Отримаємо малюнок – графік: ^^^-^- 

 

5. Розгляд та аналіз результатів таблиці записаних на дошці.

 

III. Мотивація навчальної діяльності, формування теми та мети уроку.

У шкільному підручнику з геометрії трикутнику приділяється більше уваги, ніж будь – якій іншій фігурі. Це пояснюється тим, що трикутник дуже важлива геометрична фігура, багато властивостей якої мають велике практичне значення. Вивчення властивостей багатьох інших геометричних фігур ґрунтується на знанні властивостей трикутника.

Основні властивості трикутника були відомі ще в стародавні часи; цю фігуру широко застосовували на практиці, особливо при будівництві різних споруд. Багато стародавніх документів містять зображення трикутника і задачі на трикутник. Властивості трикутника систематично викладено в « Началах» Евкліда.

Ми з вами пригадали багато цікавого про трикутник. Світ трикутників різноманітний. До того ж, трикутники можуть бути найрізноманітнішими – від маленьких, які ми будуємо в зошитах, до велетенських, які можна побудувати на поверхні Землі чи уявити, з’єднавши відрізками три зорі на небі. Для всіх цих трикутників справедлива одна й та сама властивість. Яка саме? Про це ви дізнаєтесь сьогодні на уроці.

Запишіть, будь  ласка, тему уроку « Сума кутів трикутника».

А чим на вашу думку, ми будемо займатися на сьогоднішньому уроці?

( Учні висловлюють свої думки щодо мети і завдань уроку)

Очікувана відповідь:  Вивчити теорему про суму кутів трикутника, довести її та навчитися застосовувати до розв’язування задач.

IV. Вивчення нового матеріалу.

1. Формулювання теореми про суму кутів трикутника.

2. Доведення теореми.

Доведення теореми виконаємо за алгоритмом, який записано на дошці.          ( Один учень біля дошки, а інші у зошитах доводять теорему).

а ) Пригадайте теорему, у змісті якої йшлося б про суму кутів, що дорівнює 180°. ( Якщо сума внутрішніх односторонніх кутів, утворених при перетині двох прямих січною, дорівнює 180° , то прямі паралельні. Сума суміжних кутів дорівнює 180° .)

б ) Накресліть    АВС.

в ) Проведіть через вершину А пряму МN // BC.

г ) Позначте утворені кути 1, 2, 3, 4, 5.

д ) Знайдіть внутрішні різносторонні кути на малюнку. Зробіть висновок про їх величину.

е ) Який кут утворюють в сумі кути позначені при вершині А?

є ) Чому дорівнює градусна міра   MAN?

ж) Зробіть висновок.

 

 

 

V. Застосування знань і умінь учнів на практиці.

1. Знайди третій кут     АВС, використовуючи дані таблиці.

 

			?
		?
	?

 

 

 

 

 

 

 

 

 

 

 

2. Розв’язування задач підручника

                № 236, 237, 238 (а)(усно)

                № 232 (а)( з коментуванням та записом)

                № 244(а).

                № 245(б).

I спосіб (алгебраїчний)

 

 Нехай на одну частину припадає Х.

Тоді за теоремою про суму кутів трикутника складаємо рівняння:  

2Х + 3Х +4Х =

             9Х =

              Х = : 9

              Х =

= 2 • =,   = 3 • =,   = 4 • =

II спосіб (арифметичний)

1. 2 + 3 + 4 = 9 ( частин) – становлять три кути      АВС

2. : 9 = - припадає на одну частину.

3. 20°• 2 = 40° - градусна міра    А.

4. 20°• 3 = 60° - градусна міра    В.

5.  20°• 4 = 80° - градусна міра    С.

Перевірка.     40° + 60 °+ 80° =180°

Відповідь.     = 40°,      = 60°,       = 80°.

3.   Проблемна ситуація

Той факт, що сума внутрішніх кутів трикутника дорівнює 180°, використовують багато фахівців, особливо геодезисти. Наприклад, відомо, що з пункту А відрізок ВС видно під кутом 30°, а з пункту В відрізок АС – під кутом 80° ( мал.1). Під яким кутом з пункту С видно відрізок АВ?

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Не знаючи теореми про суму кутів трикутника і безпосередньо не вимірюючи кут С , не можна відповісти на це запитання. А знаючи теорему кожний семикласник може усно обчислити результат ( учні обчислюють):     

       АСВ = 180° - ( 80° + 30°) = 180° – 110° = 70°

 

4.  Експериментальне завдання (діти працюють парами)

Обладнання: аркуш паперу, ножиці, лінійка, олівець.

Алгоритм експерименту:

  а ) накреслити на аркуші довільний     АВС;

  б ) обвести кут А однією дугою, кут В – двома, кут С – трьома;

  в ) вирізати     АВС;

  г ) вирізати кути трикутника, як показано на малюнку                               штриховою лінією

 

 

 

 

 

 

 

 

 

д ) скласти з відрізаних моделей кутів трикутника модель їх суми так, щоб вершина кутів А, В,С співпали;

е ) порівняти цю суму з розгорнутим кутом;

є ) висновок.

5. Цікаво. Французький математик Блез Паскаль довів теорему про те, що сума кутів трикутника дорівнює двом кутам столу.

 

VI. Підведення підсумків уроку.

1.  Яку найменшу кількість кутів трикутника потрібно знати (задати), щоб визначити решту кутів у випадку, коли трикутник:

• Довільний;
• Прямокутний;
• Рівнобедрений;
• Рівносторонній;

2. Всі ви вмієте розв’язувати кросворди. А я вам пропоную кросворд навпаки. У клітинках записані відповіді, а вам потрібно поставити запитання.

 

Г

Е

О

М

Е

Т

Р

І

Я

В

І

Д

Р

І

З

О

К

В

Е

Р

Ш

И

Н

А

К

У

Т

Г

Р

А

Д

У

С

Т

О

Ч

К

А

С

Т

О

Р

О

Н

А

П

Е

Р

И

М

Е

Т

Р

К

 

3. Яку властивість має будь – який трикутник?

     Прочитайте епіграф (2) і поясніть його зміст з математичної точки зору.

4. Інтерактивна вправа « Результат»

   Учні по черзі роблять висновки про те, чого вони навчилися на уроці, якого результату досягли.

5. Заповнення листка  - самооцінки.

 

Нічого не розумію                       Все розумію _________________              __________________                             Потрібна допомога         __________________________________

( Учні пишуть своє прізвище у відповідне місце)

 

6. Виставлення оцінок.

7. Розгляд малюнків виставки « Трикутна фантазія учнів 7 класу».

VII. Повідомлення домашнього завдання

1. Вивчити §15 ( формулювання теореми), на достатній і високий рівень – доведення.

2. Розв’язати задачу № 245(а), 236(в,г)(усно), 238(а).

3. Написати твір « Де я бачу геометричну фігуру трикутник?»

4. Додатково: виконати доведення теореми про суму кутів трикутника, що випливає з такого малюнка:

 

 

 

 

 

 

 

 

 

Використана література:

1. Возняк Г. М. Уроки геометрії у 7 класі.

   - Тернопіль: Підручники і посібники, 2003.

2. Бевз Г. П. Прикладна спрямованість шкільного курсу     геометрії.// Математика, № 25 – 28, 1999, - Київ.

3. Мацько Н. Д. Формування геометричних понять в учнів 4 – 5 класів: Посібник для вч. – К.: Рад. шк.., 1988.

4. Кулик Л. П. Експеримент на уроках математики.

     // Математика в школах України, № 99, 2005.

5. Лиман М. М. Школьникам о математике и математиках: Пособие для уч-ся 4 – 8 кл. сред. Школы. – М.: Просвещение, 1981.

6. Харченко Н. Розвиток критичного мислення. Інноваційні форми роботи для дітей і дорослих.

Н.Харченко;Київ : «Видавнича група “Шкільний світ” , 2018 – 120 c. (Бібліотека “Шкільного світу”).