Десятковий дріб. Запис десяткового дробу.

                                        5 клас

                                              Урок 1

Тема.  Десятковий дріб. Запис десяткових дробів.

Мета:  сформувати уявлення про десяткові дроби; домогтися засвоєння розрядів десяткового дробу; сформувати вміння читати й записувати десяткові дроби; розвивати пам`ять, логічне  мислення, пізнавальну активність;  виховувати охайність, культуру запису, увагу.

Тип уроку:  урок засвоєння нових знань, вмінь, навичок.

Обладнання:  таблиця, дошка, проектор, ноутбук.

 Хід уроку.

1. Організаційний момент.

Привітання. Перевірка готовності класу до уроку.

Вчитель

  Ви почули всі дзвінок?

  Він покликав на урок.

  Кожен з вас вже постарався,

  До уроку приготувався,

  Тож гаразд, часу не гаємо

  І урок розпочинаємо.

2. Актуалізація  опорних  знань.

   Виконання усних вправ.

1. Подайте:

а) у метрах 25 см; 3 см; 5дм.

б) у гривнях 2 коп.; 25 коп.; 10 грн 50 коп.

           2. Що спільного в запису чисел

; ;  ;  5;  ;  3;  10?

    3. Мотивація навчальної діяльності.

          Пояснення теми.

 Нарівні зі звичайними дробами для запису дробових використовують десяткові дроби. Спочатку пишуть цілу частину, а потім чисельник дробової частини; цілу частину відділяють від дробової частини комою.

  Наприклад,  7 = 7,3 (читають: «7 цілих 3 десятих»), 8 = 8,17 (читають: «8 цілих 17 сотих»).

 Цифри дробової частини ще називають десятковими знаками.

 У числа 8,17 два десяткових знаки: 1 і 7.

 Якщо дріб правильний, то перед комою пишуть цифру 0.

= 0,29.

Пояснення супроводжується комп’ютерною  презентацією.

     

 Для того, щоб записати звичайний дріб, знаменник дробової частини якого – розрядна одиниця 10, 100, 1000… у вигляді десяткового дробу,

1. записують цілу частину числа  (вона може дорівнювати 0) і ставлять кому;
2. справа від коми записують чисельник дробової частини , але він має містити стільки знаків, скільки нулів у знаменнику. Якщо в чисельнику менше знаків, ніж нулів у знаменнику, то після коми перед цифрами чисельника треба дописати таку кількість нулів, якої не вистачає.

        Наприклад,  3 = 3,041;  7 = 7,0003.

 Десяткові дроби  записуються за таким самим принципом, що й натуральні числа в десятковій системі: кожна наступна одиниця, що стоїть праворуч, у 10 разів менша від попередньої. На першому місці після коми стоїть розряд десятих, на другому – розряд сотих, на третьому – розряд тисячних і т.д.

    

 

 Десяткові дроби , як і звичайні, можна зображати на координатному промені.

 Наприклад, треба  зобразити  десятковий  дріб 0,6.

 Спочатку запишемо його у вигляді звичайного дробу: 0,6 = . Потім поділимо одиничний відрізок на 10 рівних частин. Маємо точку А, що відповідає числу 0,6, яка знаходиться праворуч від нуля на відстані шість одиничних відрізків  Аналогічно маємо точку В (1,3), що відповідає числу десятковому 1,3. Для цього поділимо відрізок між числами 1 і 2 теж на 10 рівних частин і відрахуємо 3 такі частини справа від числа 1.

Послухайте цікавий історичний матеріал про десяткові дроби, який підготував заздалегідь ваш однокласник.

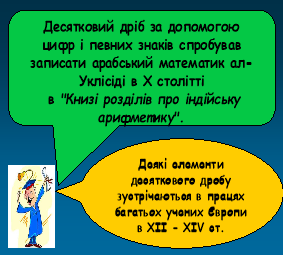
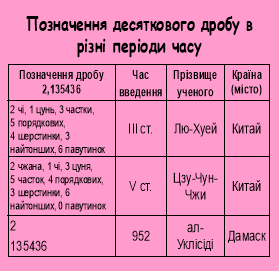
 Десяткові дроби відомі в Стародавньому Китаї  з ῙῙ ст. до н.е., про те ще й у середні віки вони не мали повної самостійності, а були пов’язані з метрологією. Китайський математик ХῙῙῙ ст. Чжу-Ші-цзе ввів термін  сяу-шу – «десятковий дріб». Ал-Уклідісі в найбільш ранній з відомих нині арабських праць «Книга розділів про індійську арифметику» (953)  висунув ідею десяткових дробів. Однак лише середньоазіатський математик і астроном     ал  ̶ Каші в праці «Ключ до арифметики»(1427) ввів десяткові дроби, подав правила дій над ними і способи перетворення  шіст десяткових дробів у десяткові й навпаки. Він цілу і дробову частину писав в один рядок, або записувати їх різними кольорами, чи ставити між ними вертикальну риску.

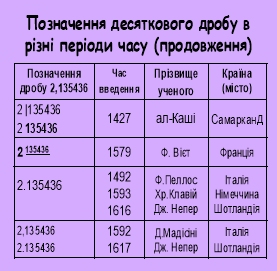
В Європі перший нарис теорії десяткових дробів з’явився у ХІV ст. (Іммануїл Бонфіс з Тараскона), а термін «десяткові дроби» замість «десяткові числа» ввів Еленд (1724). Німецький математик П. Апіан наводить (1527), з тією самою метою, що і сучасний учитель на перших уроках вивчення десяткових дробів, найпростіші випадки перетворення звичайних дробів у десяткові:  = ;  = ;  = ;  =  . У 1585 р. С.Стевін у праці «Десятина» перший в Європі (не знаючи про відкриття ал-Каші) виклав правила дій над десятковими дробами й запропонував ввести десяткову систему грошових одиниць, мір ваги. Для відокремлення цілої частини від дробової він ставив нуль у кружечку. Німецький астроном Й. Кеплер цілу і дробову частини став відокремлювати комою. Х. Клавій – крапкою (1593).

У росії десяткові дроби вперше подано в «Арифметиці» (1703) Л.Магніцького. Їм було відведено всього три сторінки, а звичайним дробам – усю другу частину книги. У російських підручниках другої половини ХVІІІ ст. десяткові дроби розглядалися вже ширше, але після звичайних дробів, коренів і логарифмів. В «Арифметиці» українського і російського математика В. Буняковського (1844) вперше десяткові дроби викладено паралельно з цілими числами перед звичайними дробами.

Перетворення звичайних дробів у десяткові і навпаки розглядав італійський математик Б. Кавальєрі (1643), у зв’язку з цим він першим в Європі став займатися періодичними дробами. Вчення про неперервні (ланцюгові) дроби бере свій початок від старогрецьких учених Теета і Евкліда. Алгоритм утворення скінчених неперервних дробів описав у праці «Вінець системи» (1150) індійський математик Бхаскара ІІ. Термін «неперервні дроби» ввів Л. Ейлер (1723).

 

Вчитель. А тепер ще й переглянемо комп’ютерну  презентацію про історію виникнення десяткових дробів.

 

1.     2.

 

 

3.     4.

 

 

 5.     6.

 

 

  7.      8.  

 

 

  9.    10.           

 

 

11.    12.

 

 

13.

 

 

Вчитель. А зараз послухайте вірш. (Читає вчитель )

 

    Десяткові дроби

 

З обчисленням дружать,

Людині вірно служать,

До послуг нам готові,

Це  – дроби десяткові.

 

Система мір метрична

Така зручна та звична,

Адже в її основі

В нас дроби десяткові.

 

Нам робить калькулятор

Обчислення чудові,

А на його екрані –

Теж дроби десяткові.

 

Цифри в дробу йдуть підряд:

За розрядом йде розряд.

Якщо правила ти знаєш,

Дріб запишеш, прочитаєш,

 

Зможеш дроби порівняти,

І додати, і відняти,

А крім того можна, діти,

І округлення робити.

 

Ці дії з десятковими дробами ми з вами, діти, будемо вивчати на наступних уроках.

 

3. Закріплення теми. 

                                                                                                                                           Підручник О.С. Істер «Математика 5 клас». 2013р.

 

№ 1123 (усно),

№ 1124 (усно).

№ 1125

Запиши десятковим дробом:

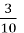1. = 0,3;  4) 1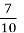= 1,7;  7) 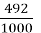= 0,492
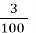2. = 0,03  5) 5 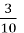= 5,3;         8) 2 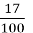= 2,17;
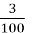3. = 0,003           6) 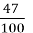= 0,47          9)15 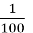=15,01;

     10) 17= 17,012 11) 8 = 8,173  12) 152 = 152,007.

 

№1127

Запиши десятковим дробом:

 1)25,8;   2) 0,9;   3) 9,72;   4) 0,82;   5) 115,057;   6) 0,003.

 

     Фізкультхвилинка

 

Трава низенька – низенька,

Дерева високі – високі,

Вітер дерева колише – гойдає.

То вправо, то вліво нахиляє.

То вгору, то назад.

То вниз нагинає.

 Птахи летять, відлітають,

А учні тихенько за парти сідають.

 

№ 1129

Замість зірочок запиши таке число, щоб рівність була правильною:

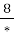1. = 0,8  2) 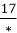= 0,17           3) 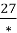= 0,027     4) 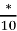= 0,7

    = 0,8     = 0,17              = 0,027                = 0,7

 

     5) = 0,02  6) = 0,012 

  = 0,02               = 0,012.

 

№1135

Запиши у вигляді правильного дробу або мішаного числа:

1) 2,7 = 2;         3) 413,03 = 413;              5) 0,301 = ;

 

2) 41,21 = 41        4)  5,007 = 5;              6) 0,099 = .

 

№ 1137

Яким десятковим дробам відповідають точки А, В, С, Д, Е?

 

А (0,4); С (0,7); Д (1,1); Е (1,6); В (2,2).

 

5. Підсумок уроку. Домашнє завдання.

 

 Що нового дізналися на уроці?

 Який момент був найцікавіший?

 Який найскладніший?

 

Додому:  вивчити  §34, ст.248, № 1126, № 1136, № 1139.