Дії над векторами у просторі. Презентація
Про матеріал
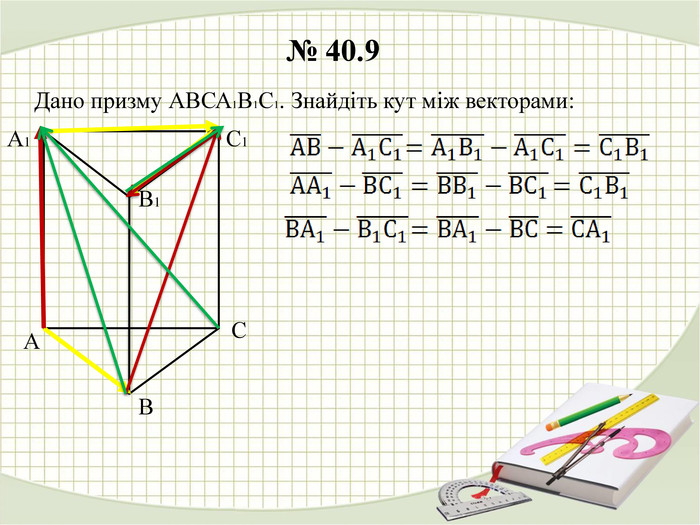
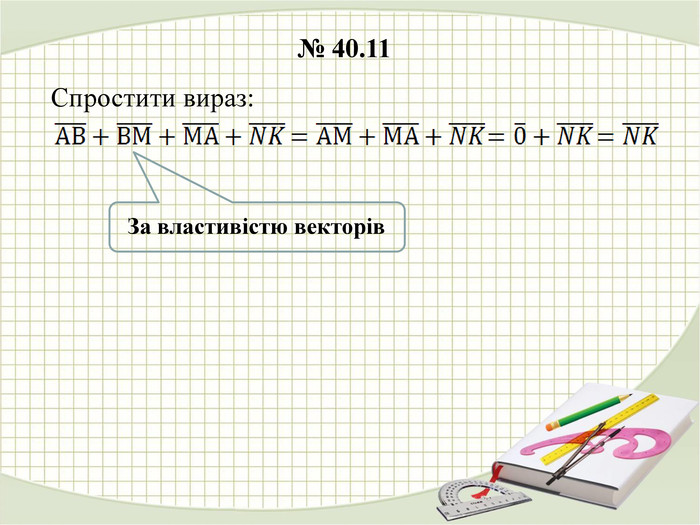
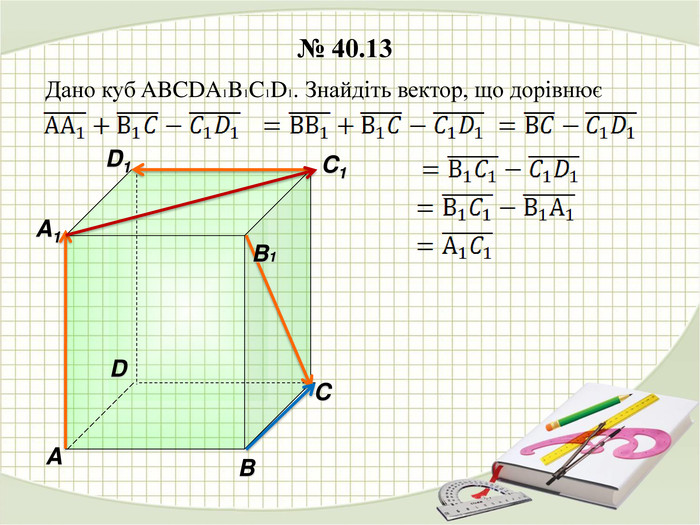
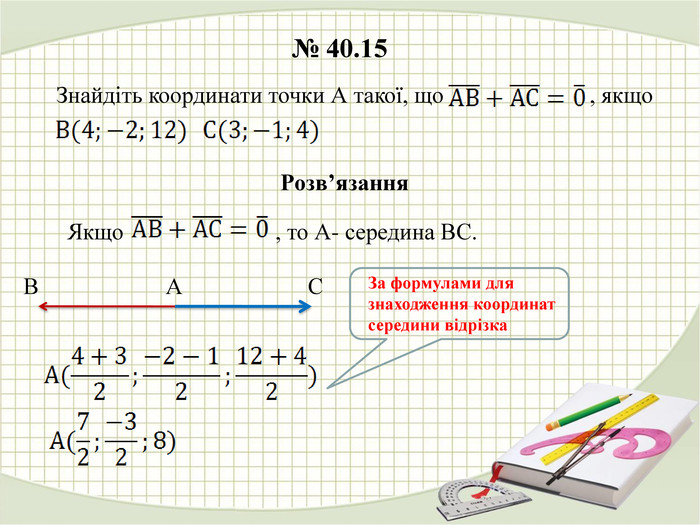
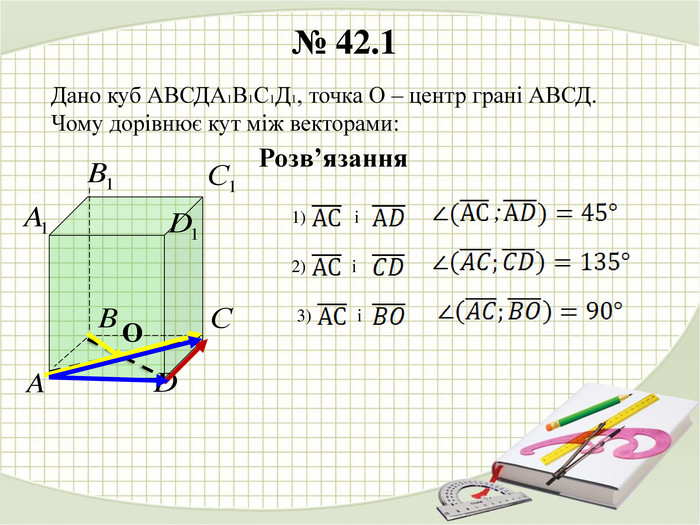
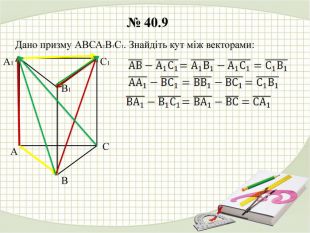
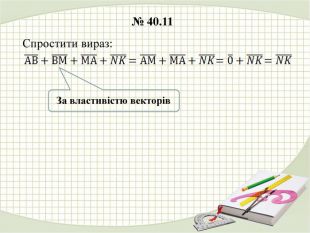
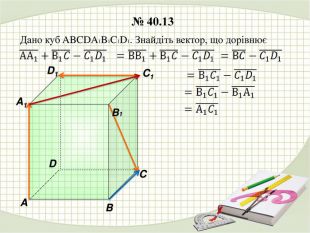
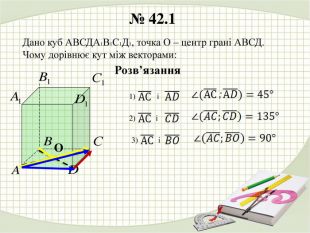
У презентації наведено розв'язання деяких задач з теми "Дії над векторами у просторі" Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
ppt
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку