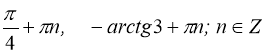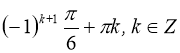Тригонометричні функції

Контрольна робота «Тригонометричні функції їх властивості»

І варіант

У завданнях 1-6 оберіть правильну відповідь

1.Чому дорівнює:  cos 150°    ?

  а)   ;        б) ;        в) - ;   г) інша відповідь.

2. Знайти правильну рівність:

 

а)рад=180° ;  б) рад=150°;      в) рад=120°;  г) інша відповідь.

3. Обчислити значення cosх , якщо: sinх=0,6  ,   <х < π

 а) 0,8 ;     б) -0,8;          в) ±0,8; г) інша відповідь.

4. Позначте правильне висловлювання:

а) sin 45° > sin 135°;  б) cos  30°> cos  120°;

 в) tg 190°<0;   г) інша відповідь

5. Обчислити:  arctg (- ) + arctg 0

а)  ;  б) -;          в) ;  г) інша відповідь.

 6.  Спростити вираз: - sinх - cosх

 а) -1 + tg х;   б) - sіп х;    в) 1- tg х;  г) інша відповідь.

 

 

 

 

 

 

8. Розв’язати рівняння :

 

 

 

 

 

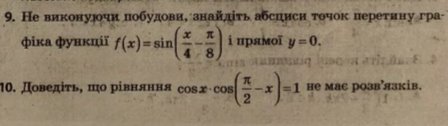
Контрольна робота «Тригонометричні функції їх властивості»

ІІ варіант

У завданнях 1-6 оберіть правильну відповідь

1. Чому дорівнює: sin 150°   ?

   а) ;       б) ;          в) - ;       г) інша відповідь

2. Позначте правильне висловлювання:

а) sin 170° > sin 80°;   б) cos  30°> cos  10°;

в) ctg 190°<0;    г) інша відповідь.

3. Знайти правильну рівність:

а) рад=60°; б) рад=270°;      в) рад=180°;г) інша відповідь.

4. Обчислити значення cosх, якщо:

    sinх=0,8;  0°<х < 180°         

 а) -0,6; б) ±0,6;        в) -0,6;  г) інша відповідь.

.

5. Обчислити:  tg (arc sin 0) + arc cos

а)  ; б)  ;            в) ;  г) інша відповідь.

 

6. Спростити вираз: (1+ tg х )  cosх+ tg х

 

 

 

 

 

 

8. Розв’язати рівняння :

 

 

 

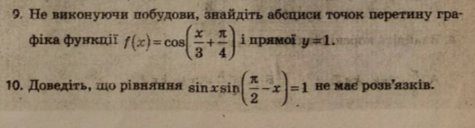
 Контрольна робота «Тригонометричні функції їх властивості»

У завданнях 1-6 оберіть правильну відповідь

 

ІІІ варіант

1. Чому дорівнює:  ctg 150°  ?

     а)    ;      б) ;     в) - ;    г) інша відповідь.

2. Позначте правильне висловлювання:

 а) sin 125° > sin 25° ; б) cos  30°> cos  130°; 

 в) sin 190° > 0 ;  г) інша відповідь. 

3. Обчислити значення cos, якщо: sin=0,6; 0°< < 180°         

 а) 0,8;       б) ±0,8;       в) -0,8;  г) інша відповідь.

4. Знайти правильну рівність:

а) рад=180° ;     б) рад=150°;      в) рад=120°;  г) інша відповідь.

5. Розв’язати рівняння:  сtg  х = -

а)   + πп, ;   б) - +πп, ; 

 в)  + πп, ;   г) інша відповідь.

6. Обчислити:  сtg (arc cos 0 ) - arc cos (-)

а)  ; б)  -;      в) ; г) інша відповідь.

 

 

4. Спростити вираз: сtg х (1+ tg х ) -

    а) 1; б) 0;         в) 2sin х  г) інша відповідь.

 

 

 

 

 

 

 

 

 

 

 

 

ВПРАВИ НА ЗАКРІПЛЕННЯ

 

Рівняння	Відповідь
1.
2.
3.
4.
5.

 

 

Тригонометричні рівняння виду називаються однорідними першого степеня, тригонометричні рівняння виду називаються однорідними другого степеня.

  Якщо то  дістанемо, що .  Але одночасно і не можуть дорівнювати нулю, тому при рівняння не має коренів.

 Якщо то, поділивши обидві частини рівняння  на , дістанемо рівняння рівносильне даному:

Приклад 1. Розв’язати рівняння: .

Розв’язання:

Розділивши обидві частини рівняння на , отримаємо:

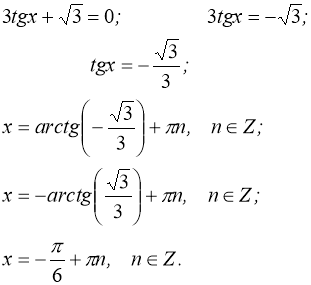
Відповідь: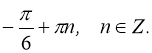  

Приклад 2.     Розв’язати рівняння:

Розв’язання:

Розділивши обидві частини рівняння на , отримаємо рівняння:

Нехай Тоді

                    

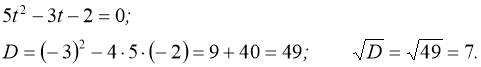
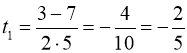
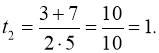
Повертаючись до заміни, матимемо:

.

            

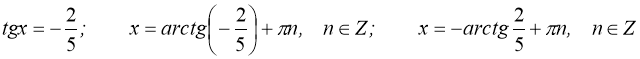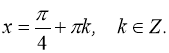
Відповідь:  ,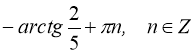        

 

 

4.  Розв’язати рівняння:  sin х = 0,5

       а)  ± +2 πп, п є  Z ;б) (-1) +πп,  п є  Z; в) +2 πп; п є  Z; г) інша відповідь.